机器人学习-路径规划实验（一）

1.简介

本实验任务：编写前面学过的两个路径规划算法。

首先用C++编写Breadth-first搜索算法。该算法分为不同的编码测验，最终生成机器人从起点移动到目标的最短路径。

然后，将继续进行必要的更改，以编写A*算法。在对BFS和A*算法进行编码之后，将可视化地比较生成的扩展列表。仔细检查后，判断哪种算法更有效。

在本实验的后面部分，将把A*算法应用到现实世界的问题中。实际问题只是使用占用网格映射算法生成的地图。

实验:路径规划

实验的详细步骤列表如下:

2.建模问题
本实验的目的是利用不同的路径规划算法，为机器人在5x6地图中从起始位置移动到目标位置找到最短路径。机器人只能向四个方向移动:上、左、下、右。我们将首先使用C++中的类来建模这个问题，然后用BFS和A*算法来解决它。

Given

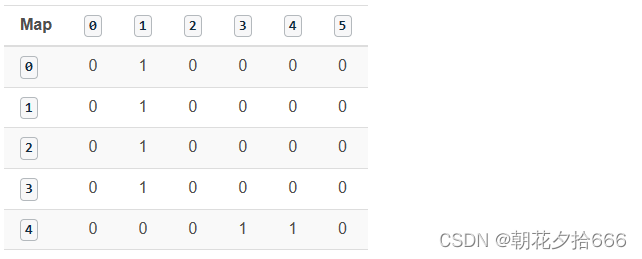
Grid(5x6):

0 1 0 0 0 0
0 1 0 0 0 0
0 1 0 0 0 0
0 1 0 0 0 0
0 0 0 1 1 0

其中1代表障碍，0代表自由空间。

机器人起始位置:0,0

机器人目标位置:4,5

移动方向:上(-1,0)-左(0，-1)-下(1,0)-右(0,1)

移动方向矢量是四个不同2D矢量的集合，每个矢量都允许在地图中的网格单元之间移动。

移动箭头:上(^)-左(<)-下(v) -右(>)

移动箭头向量存储机器人的动作，这个向量将在本实验室稍后使用，以可视化机器人在最短路径上的每个网格单元的方向。

移动成本:1

移动成本值表示从一个单元格移动到另一个单元格的成本。在这里，对于所有可能的移动，代价都是相等的。

测试
在这个测试中，为了建模问题，有三个主要任务要完成:

注意
在整个实验过程中，将使用C++中的1D和2D向量。vector允许使用预先构建的函数轻松地管理和操作数据。例如:pop_back函数可用于删除vector中的最后一个元素。

关于向量，可参阅以下两个资源:

1. 2D Vectors: 学习如何在C++中定义和使用2D向量。
2. Documentation: 学习向量迭代器和修饰器（modifiers）。

参考代码如下： 

#include <iostream>
#include <string.h>
#include <vector>
#include <algorithm>

using namespace std;

/* TODO: Define a Map class
   Inside the map class, define the mapWidth, mapHeight and grid as a 2D vector
*/
class Map {
public:
    const static int mapWidth = 6;
    const static int mapHeight = 5;
    vector<vector<int> > grid = {
        { 0, 1, 0, 0, 0, 0 },
        { 0, 1, 0, 0, 0, 0 },
        { 0, 1, 0, 0, 0, 0 },
        { 0, 1, 0, 0, 0, 0 },
        { 0, 0, 0, 1, 1, 0 }
    };
};  

/* TODO: Define a Planner class
   Inside the Planner class, define the start, goal, cost, movements, and movements_arrows
   Note: The goal should be defined it terms of the mapWidth and mapHeight
*/
class Planner : Map {
public:
    int start[2] = { 0, 0 };
    int goal[2] = { mapHeight - 1, mapWidth - 1 };
    int cost = 1;

    string movements_arrows[4] = { "^", "<", "v", ">" };

    vector<vector<int> > movements{
        { -1, 0 },
        { 0, -1 },
        { 1, 0 },
        { 0, 1 }
    };
};
/* TODO: Define a print2DVector function which will print 2D vectors of any data type
   Example
   
   Input: 
   vector<vector<int> > a{
  
  { 1, 0 },{ 0, 1 }};
   print2DVector(a);
   vector<vector<string> > b{
  
  { "a", "b" },{ "c", "d" }};
   print2DVector(b);
   
   Output:
   1 0
   0 1
   a b
   c d
   Hint: You need to use templates
*/
template <typename T>
void print2DVector(T Vec)
{
    for (int i = 0; i < Vec.size(); ++i) {
        for (int j = 0; j < Vec[0].size(); ++j) {
            cout << Vec[i][j] << ' ';
        }
        cout << endl;
    }
}
/*############ Don't modify the main function############*/
int main()
{
    // Instantiate map and planner objects
    Map map;
    Planner planner;

    // Print classes variables
    cout << "Map:" << endl;
    print2DVector(map.grid);
    cout << "Start: " << planner.start[0] << " , " << planner.start[1] << endl;
    cout << "Goal: " << planner.goal[0] << " , " << planner.goal[1] << endl;
    cout << "Cost: " << planner.cost << endl;
    cout << "Robot Movements: " << planner.movements_arrows[0] << " , " << planner.movements_arrows[1] << " , " << planner.movements_arrows[2] << " , " << planner.movements_arrows[3] << endl;
    cout << "Delta:" << endl;
    print2DVector(planner.movements);

    return 0;
}

3.BFS:扩展列表
现在使用C++中的Map和Planner类对问题进行建模，接下来将从BFS算法的第一部分开始。在这个测试中，编写搜索函数，以最低的代价扩展单元格，直到达到目标。

为此，需要用三元组值[g, x, y]表示每个单元格，其中g表示向该单元格扩展的总代价，x是行值，y是列值。

一旦扩展到达目标，打印目标的最终三重值。

在编写搜索函数时，记住以下事项

• 当扩展到一个新的单元格时，检查是否达到了目标;一旦到达，打印它的三重值。
• 主动检查是否遇到了障碍。如果遇到了障碍，停止扩展并打印一条消息，表明未能达到目标。
• 展开g值最低的单元格，并将展开存储在一个开放向量中。如果两个单元格的g值相等，则可以选择其中一个单元格进一步展开。

提示
下面是如何使用BFS算法扩展单元，直到达到目标:

Expansion #: 0
Open List: [0 0 0 ]
Cell Picked: [0 0 0]

---

Expansion #: 1
Open List: [1 1 0 ]
Cell Picked: [1 1 0]

---

Expansion #: 2
Open List: [2 2 0 ]
Cell Picked: [2 2 0]

---

Expansion #: 3
Open List: [3 3 0 ]
Cell Picked: [3 3 0]

---

Expansion #: 4
Open List: [4 4 0 ]
Cell Picked: [4 4 0]

---

Expansion #: 5
Open List: [5 4 1 ]
Cell Picked: [5 4 1]

---

Expansion #: 6
Open List: [6 4 2 ]
Cell Picked: [6 4 2]

---

Expansion #: 7
Open List: [7 3 2 ]
Cell Picked: [7 3 2]

---

Expansion #: 8
Open List: [8 3 3 ], [8 2 2 ]
Cell Picked: [8 2 2]

---

Expansion #: 9
Open List: [9 2 3 ], [9 1 2 ], [8 3 3 ]
Cell Picked: [8 3 3]

---

Expansion #: 10
Open List: [9 3 4 ], [9 2 3 ], [9 1 2 ]
Cell Picked: [9 1 2]

---

Expansion #: 11
Open List: [10 1 3 ], [10 0 2 ], [9 3 4 ], [9 2 3 ]
Cell Picked: [9 2 3]

---

Expansion #: 12
Open List: [10 2 4 ], [10 1 3 ], [10 0 2 ], [9 3 4 ]
Cell Picked: [9 3 4]

---

Expansion #: 13
Open List: [10 3 5 ], [10 2 4 ], [10 1 3 ], [10 0 2 ]
Cell Picked: [10 0 2]

---

Expansion #: 14
Open List: [11 0 3 ], [10 3 5 ], [10 2 4 ], [10 1 3 ]
Cell Picked: [10 1 3]

---

Expansion #: 15
Open List: [11 1 4 ], [11 0 3 ], [10 3 5 ], [10 2 4 ]
Cell Picked: [10 2 4]

---

Expansion #: 16
Open List: [11 2 5 ], [11 1 4 ], [11 0 3 ], [10 3 5 ]
Cell Picked: [10 3 5]

---

Expansion #: 17
Open List: [11 4 5 ], [11 2 5 ], [11 1 4 ], [11 0 3 ]
Cell Picked: [11 0 3]

---

Expansion #: 18
Open List: [12 0 4 ], [11 4 5 ], [11 2 5 ], [11 1 4 ]
Cell Picked: [11 1 4]

---

Expansion #: 19
Open List: [12 1 5 ], [12 0 4 ], [11 4 5 ], [11 2 5 ]
Cell Picked: [11 2 5]

---

Expansion #: 20
Open List: [12 1 5 ], [12 0 4 ], [11 4 5 ]
Cell Picked: [11 4 5]

参考代码如下： 

#include <iostream>
#include <string.h>
#include <vector>
#include <algorithm>

using namespace std;

// Map class
class Map {
public:
    const static int mapWidth = 6;
    const static int mapHeight = 5;
    vector<vector<int> > grid = {
        { 0, 1, 0, 0, 0, 0 },
        { 0, 1, 0, 0, 0, 0 },
        { 0, 1, 0, 0, 0, 0 },
        { 0, 1, 0, 0, 0, 0 },
        { 0, 0, 0, 1, 1, 0 }
    };
};

// Planner class
class Planner : Map {
public:
    int start[2] = { 0, 0 };
    int goal[2] = { mapHeight - 1, mapWidth - 1 };
    int cost = 1;

    string movements_arrows[4] = { "^", "<", "v", ">" };

    vector<vector<int> > movements{
        { -1, 0 },
        { 0, -1 },
        { 1, 0 },
        { 0, 1 }
    };
};

// Template function to print 2D vectors of any type
template <typename T>
void print2DVector(T Vec)
{
    for (int i = 0; i < Vec.size(); ++i) {
        for (int j = 0; j < Vec[0].size(); ++j) {
            cout << Vec[i][j] << ' ';
        }
        cout << endl;
    }
}

/*#### TODO: Code the search function which will generate the expansion list ####*/
// You are only required to print the final triplet values
void search(Map map, Planner planner)
{
    // Create a closed 2 array filled with 0s and first element 1
    vector<vector<int> > closed(map.mapHeight, vector<int>(map.mapWidth));
    closed[planner.start[0]][planner.start[1]] = 1;

    // Defined the triplet values
    int x = planner.start[0];
    int y = planner.start[1];
    int g = 0;

    // Store the expansions
    vector<vector<int> > open;
    open.push_back({ g, x, y });

    // Flags
    bool found = false;
    bool resign = false;

    int x2;
    int y2;

    // While I am still searching for the goal and the problem is solvable
    while (!found && !resign) {
        // Resign if no values in the open list and you can't expand anymore
        if (open.size() == 0) {
            resign = true;
            cout << "Failed to reach a goal" << endl;
        }
        // Keep expanding
        else {
            // Remove triplets from the open list
            sort(open.begin(), open.end());
            reverse(open.begin(), open.end());
            vector<int> next;
            // Stored the poped value into next
            next = open.back();
            open.pop_back();

            x = next[1];
            y = next[2];
            g = next[0];
            
            // Ch