线性规划求解——DRS算法

原问题

$$\begin{gathered} \underset{x}{\min }{c}^{T}x \\ s.t.Ax=b \\ x\ge 0\text{\hspace{1em}(1)} \end{gathered}$$

对偶问题

$$\begin{gathered} \underset{y}{\max }{b}^{T}y \\ s.t.A^{T}y+s=c \\ s\ge 0\text{\hspace{1em}(2)} \end{gathered}$$
$A\in {\mathbb{R}}^{m\times n},x\in {\mathbb{R}}^n,s\in {\mathbb{R}}^n,y\in {\mathbb{R}}^m$

---

DRS算法

考虑优化问题：$$\underset{x}{\min }f(x)=g(x)+h(x)$$其中 $g(x)$ 和 $h(x)$ 均为闭凸函数。

Douglas-Rachford 迭代

从任意初始点 $z^{(0)}$， 重复以下步骤：$$x^k=pro{x}_{th}(z^{k-1})$$$$y^k=pro{x}_{tg}(2x^k-z^{k-1})\text{\hspace{1em}(3)}$$$$z^k=z^{k-1}+y^k-x^k$$ 直至收敛。

注：
$$pro{x}_f(x)=arg\underset{u}{\min }f(u)+\frac{1}{2}||u-x|{|}_2^2$$
$$\begin{gathered} pro{x}_{tf}(x)=arg\underset{u}{\min }tf(u)+\frac{1}{2}||u-x|{|}_2^2 \\ =arg\underset{u}{\min }f(u)+\frac{1}{2t}||u-x|{|}_2^2 \end{gathered}$$

---

言归正传，针对线性规划的原问题，将其写成无约束优化问题：$$\underset{x}{\min }{c}^{T}x+{\mathbb{I}}_{Ax=b}(x)+{\mathbb{I}}_{x\ge 0}(x)$$其中 ${\mathbb{I}}_S$ 表示集合 $S$ 的示性函数，即$${\mathbb{I}}_S(x)=\{\begin{array}{lr}0,x\in S& \\ \infty ,otherwise& \end{array}$$因此可以将目标函数拆分成两部分：$$\begin{gathered} g(x)=c^{T}x+{\mathbb{I}}_{Ax=b}(x) \\ h(x)={\mathbb{I}}_{x\ge 0}(x) \end{gathered}$$然后利用 Douglas-Rachford 迭代即可求出问题的解 $x$。

下面来看具体细节：$pro{x}_{tg}$ 和 $pro{x}_{th}$ 解析表达式是什么？

先来看简单的：$$pro{x}_{th}(x)=arg\underset{u}{\min }h(u)+\frac{1}{2t}||u-x|{|}_2^2$$也就是说 $pro{x}_{th}(x)$ 是在固定 $x$ 时下述问题的解：$$\begin{gathered} \underset{u}{\min }\frac{1}{2t}||u-x|{|}_2^2 \\ s.t.u\ge 0 \end{gathered}$$说白了，就是 $x$ 在第一象限的投影！所以$$pro{x}_{th}(x)=max(x,0)\text{\hspace{1em}(4)}$$
接下来稍复杂，$pro{x}_{tg}(x)$ 是在固定 $x$ 时下述问题的解：$$\begin{gathered} \underset{u}{\min }{c}^{T}u+\frac{1}{2t}||u-x|{|}_2^2 \\ s.t.Au=b \end{gathered}$$
写出拉格朗日函数：$$L(u,\lambda )=c^{T}u+\frac{1}{2t}||u-x|{|}_2^2+{\lambda }^T(Au-b)$$由最优性条件：$$\begin{gathered} 0={\nabla }_{u}L=c+A^T\lambda +\frac{1}{t}(u-x) \\ \Rightarrow u=x-t(c+A^T\lambda ) \end{gathered}$$代入约束条件：$$\begin{gathered} 0=Au-b=Ax-tAc-tA{A}^T\lambda -b \\ \Rightarrow \lambda =(tA{A}^T{)}^{-1}(A(x-tc)-b) \end{gathered}$$解得$$u=x-t(c+A^T\lambda )=x-t(c+A^T(tA{A}^T{)}^{-1}(A(x-tc)-b))$$即$$pro{x}_{tg}(x)=x-t(c+A^T(tA{A}^T{)}^{-1}(A(x-tc)-b))\text{\hspace{1em}(5)}$$

将 (4)(5) 代入 Douglas-Rachford 迭代(3)，便是求解的全过程。

上代码！

function [x] = LP_DRS_primal(c, A, b, opts, x0)

m = size(A,1);
n = size(A,2);

z = randn(n,1);  %随机初始化
x = x0;   % 随机初始化

S = A*A';
U = chol(S);
L = U'; %cholesky decomposition: S = L*U = U'*U

t = 0.1; % 超参数
prox_th = @(x) max(x,0);
prox_tg = @(x) x-t*(c+A'*((t*U)\(L\(A*(x-t*c)-b))));

err = 1;
x_old = x;
while(err > 1e-6)
    
   x = prox_th(z);
   
   y = prox_tg(2*x-z);
   
   z = z + y - x;
    
   err = norm(x-x_old);
   x_old = x;
end

end

看效果！

% 生成数据
n = 100;
m = 20;
A = rand(m,n);
xs = full(abs(sprandn(n,1,m/n)));
b = A*xs;
y = randn(m,1);
s = rand(n,1).*(xs==0);
c = A'*y + s;

% 计算误差
errfun = @(x1, x2) norm(x1-x2)/(1+norm(x1));

% 标准答案
figure(1);
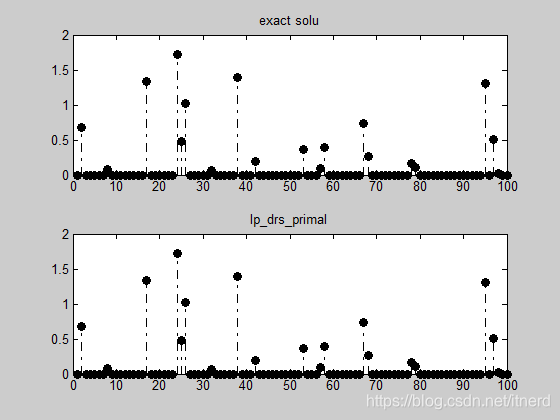
subplot(2,1,1);
stem(xs,'fill','k-.')
title('exact solu');

% DRS 求解
opts = [];
tic;
[x1] = LP_DRS_primal(c, A, b, opts, x0);
t1 = toc;
subplot(2,1,2);
stem(x1,'fill','k-.');
title('lp_drs_primal');

fprintf('lp-drs-primal: cpu: %5.2f, err-to-exact: %3.2e\n', t2, errfun(x1, xs));

看速度！

lp-drs-primal: cpu:  0.14, err-to-exact: 2.92e-04