谱聚类

谱聚类算法：¹

针对如下数据：

import matplotlib.pyplot as plt

def gen_ring(r, var, num):
    r_array = np.random.normal(r,var,num)
    t_array = [ np.random.random()*2*np.math.pi for i in range(num)]
    data = [[r_array[i]*np.math.cos(t_array[i]),
             r_array[i]*np.math.sin(t_array[i])] 
            for i in range(num)]
    return data

def gen_gauss(mean,cov,num):     
    return np.random.multivariate_normal(mean,cov,num)
    
def gen_clusters():
    data = gen_ring(1,0.1,100)
    data = np.append(data,gen_ring(3,0.1,300),0)
    data = np.append(data,gen_ring(5,0.1,500),0)
    mean = [7,7]
    cov = [[0.5,0],[0,0.5]]
    data = np.append(data,gen_gauss(mean,cov,100),0)
    return np.round(data,4)

def show_scatter(data,colors):
    cm = plt.cm.get_cmap('Spectral')
    x,y = data.T
    plt.scatter(x,y,c=colors,cmap=cm)
    plt.axis()
    plt.xlabel("x")
    plt.ylabel("y")

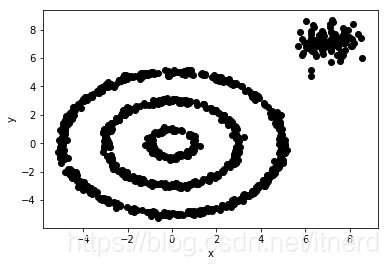
data = gen_clusters()
show_scatter(data,'k')
plt.show()



import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans

# 径向基函数 计算相似度
def affinity(a,b):
    one_over_2sigma2 = 10
    return np.math.exp(-one_over_2sigma2*np.dot(a-b,a-b))

# 前 k 大特征值对应的 k 个特征向量
def topk(mat,k):
    e_vals,e_vecs = np.linalg.eig(mat)
    sorted_indices = np.argsort(e_vals)
    return e_vals[sorted_indices[:-k-1:-1]],e_vecs[:,sorted_indices[:-k-1:-1]]

data = gen_clusters()

# 每个点之间的相似度
A = np.matrix([[affinity(i,j) for i in data] for j in data])

# 此处D对应算法中 D^{-1/2}
D = np.matrix(np.sqrt(np.diag(np.sum(A,axis=1).flatten().getA()[0]))).I

# 对应算法中的 L
L = D.dot(A).dot(D)

# 前 4 个特征向量
vals,X = topk(L,4)

# Y 具有单位行向量的
Y = np.matrix(np.diag(np.sqrt(np.sum(np.multiply(X,X),axis=1)).flatten().getA()[0])).I.dot(X)

# 用 K-Means 对Y的行向量聚类
estimator = KMeans(init='k-means++', n_clusters=4, n_init=4)
estimator.fit(Y)
label2color = ['r','g','b','k']
colors = [label2color[i] for i in estimator.labels_]
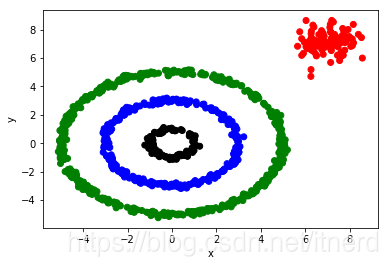
show_scatter(data,colors)
plt.show()

结果如下：

---

1. Ng A Y, Jordan M I, Weiss Y. On spectral clustering: analysis and an algorithm[J]. Proc Nips, 2001, 14:849–856. ↩︎