文章目录
总览
“如果你不能把它解释地足够简洁,说明你还不够理解它。” —— 阿尔伯特·爱因斯坦
关于作者
我叫Alex Becker,我来自以色列。我是一名在无线领域有着超过20年经验的工程师。我工作的一部分便是和卡尔曼滤波器打交道,主要应用于目标跟踪。
我始终接受建设性的批评,我很乐意倾听你的评价和建议。如有需要请给我发邮件。
免责声明:本教程的所有数值示例所体现和涉及到的、包括但不限于设计模式、方法论、技术和参数等,与作者已知或从事的任何应用系统均无关。
关于卡尔曼滤波
许多现代系统均使用多个传感器的多个测量结果来估计隐藏(未知)状态。例如GPS接收机能够用来估计位置和速度,此处位置和速度就是隐藏状态,接收到的卫星信号时差就构成了一组测量。
对跟踪和控制系统而言,最大的挑战之一便是在存在不确定性的情况下获取一个对隐藏状态的精准的估计。例如GPS接收机会受各种外部干扰,如热噪声、大气效应、卫星轨道微小变化、接收机时间精度等。
卡尔曼滤波是最常用最重要的状态估计算法之一。卡尔曼滤波器能从不确定且非精确的测量中估计隐藏状态,同时还可以根据历史估计值对未来系统状态进行预测。
这种滤波算法以 Rudolf E. Kálmán (1930年5月19日 - 2016年7月2日) 的名字命名。在1960年,卡尔曼发表了著名的论文,描述了一个离散数据的线性滤波问题的递归解法。
如今卡尔曼滤波广泛应用于目标追踪、定位和导航系统、控制系统、计算机图形学等等许多领域。

为什么需要预测算法
在开始讲解卡尔曼滤波以前,我们先闹明白为什么需要一套跟踪和预测算法。
为说明这一点,我们拿一个目标追踪雷达来举例。
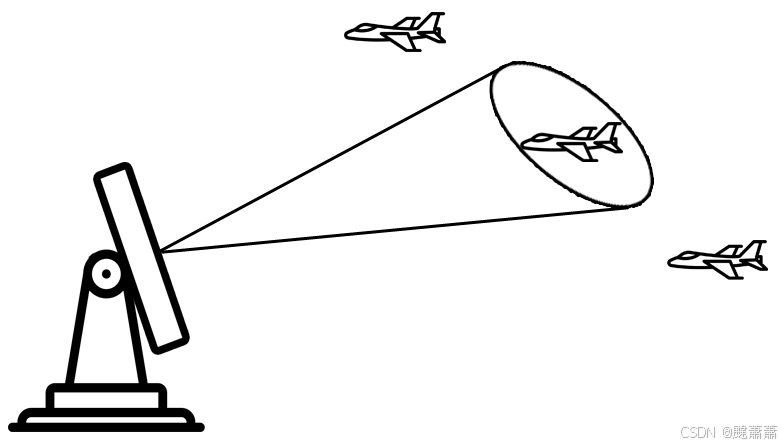
假设我们每5秒发起一次追踪,即以5秒为间隔,雷达发出一束波束照射目标。
雷达波到达目标并返回后,它开始估计目标当前的位置和速度。雷达同时还能估计(或预测)目标在下一个测量周期即5秒后的位置。
目标未来的位置可以通过牛顿运动方程得到:
x
=
x
0
+
v
0
Δ
t
+
1
2
a
Δ
t
2
x= x_{0} + v_{0} \Delta t+ \frac{1}{2}a \Delta t^{2}
x=x0+v0Δt+21aΔt2其中:
x
x
x 是目标位置
x
0
x_{0}
x0 是初始目标位置
v
0
v_{0}
v0 是初始目标速度
a
a
a 是目标加速度
Δ
t
\Delta t
Δt 是采样周期(本例中为5秒)
处理三维空间中的运动时,牛顿运动方程可以以方程组形式给出:
{
x
=
x
0
+
v
x
0
Δ
t
+
1
2
a
x
Δ
t
2
y
=
y
0
+
v
y
0
Δ
t
+
1
2
a
y
Δ
t
2
z
=
z
0
+
v
z
0
Δ
t
+
1
2
a
z
Δ
t
2
\left\{\begin{array}{l} x= x_{0} + v_{x0} \Delta t+ \frac{1}{2}a_{x} \Delta t^{2}\\[1em] y= y_{0} + v_{y0} \Delta t+ \frac{1}{2}a_{y} \Delta t^{2}\\[1em] z= z_{0} + v_{z0} \Delta t+ \frac{1}{2}a_{z} \Delta t^{2} \end{array}\right.
⎩
⎨
⎧x=x0+vx0Δt+21axΔt2y=y0+vy0Δt+21ayΔt2z=z0+vz0Δt+21azΔt2
这组目标的参数
[
x
,
y
,
z
,
v
x
,
v
y
,
v
z
,
a
x
,
a
y
,
a
z
]
\left[ x, y, z, v_{x},v_{y},v_{z},a_{x},a_{y},a_{z} \right]
[x,y,z,vx,vy,vz,ax,ay,az] 称为 系统状态。当前状态作为预测算法的输入,预测算法的输出则是目标未来的状态,即目标在下一个采样点所具有的参数。
上面的牛顿运动方程组称为 动态模型 或 状态空间模型。动态模型描述了预测算法的输入和输出之间的关系。
显然,如果目标当前的状态和动态模型是已知的,预测目标后续的状态就可以很简单地实现。
实际中,雷达的测量并不完全准确,它所包含的随机噪声或不确定性会影响对目标状态的预测的精准度。误差大小取决于多方面因素,例如雷达校准、波束宽度、回波的信噪比等。雷达测量的随机噪声或不确定性称为 测量噪声。
另外,由于存在风扰、飞行员干预等因素,目标的运动并不总能依照运动方程。运动方程预测和实际目标的运动轨迹之间的差异称为 过程噪声。
由于测量噪声和过程噪声的存在,估计的目标位置有可能和目标的真实位置大相径庭。这种情况下,雷达的波束完全可能指向错误的方位,从而跟丢目标。
为了提升雷达跟踪的精准度,一套能对抗测量和模型的不确定性的预测算法就至关重要。
最常用的跟踪和预测算法就是 卡尔曼滤波。
KALMAN滤波简介
必要的背景知识
在开始之前,我想先解释几个基本用语,例如方差、标准差、正态分布、估计、准度、精度、均值、期望,和随机变量。
本教程的读者应该大部分已经对统计学比较熟悉。但在本教程的开始我承诺过会提供一些理解卡尔曼滤波器所需的背景知识。因此如果你对统计学已经比较熟悉,可以跳过这一章内容直接开始下一章。
均值和期望
均值 Mean 和 期望 Expectation 是密切相关但有所不同的概念。
举个例子,给你五枚硬币 - 两个5分硬币和三个10分硬币,我们可以轻松地计算出这些硬币面值的均值,即求它们面值的平均数。

V
m
e
a
n
=
1
N
∑
n
=
1
N
V
n
=
1
5
(
5
+
5
+
10
+
10
+
10
)
=
8
c
e
n
t
s
V_{mean}= \frac{1}{N} \sum _{n=1}^{N}V_{n}= \frac{1}{5} \left( 5+5+10+10+10 \right) = 8cents
Vmean=N1n=1∑NVn=51(5+5+10+10+10)=8cents
因为本系统中的状态(硬币面值)直接写在了硬币上,并且就是真实值,不存在任何不确定性,因此我们可以使用全量样本(全部五个硬币)的真实值来计算平均值,此时的平均值并不是期望。

假设给同一个人的体重进行五次测量,得到五个不同的测量值:79.8kg,80kg,80.1kg,79.8kg和80.2kg。将这个人看作一个系统,他/她的体重就是该系统的状态。
五次测量值之所以各不相同是因为体重秤存在随机测量误差。其实想一想就能知道,我们无法得知体重的真值,因为它是一个所谓隐藏状态(译注:原文为Hidden State,意为客观存在但是无法直接读取的能观状态)。但是我们可以通过对体重秤的多次测量值求平均来对这个真值进行估计。
W
=
1
N
∑
n
=
1
N
W
n
=
1
5
(
79.8
+
80
+
80.1
+
79.8
+
80.2
)
=
79.98
k
g
W = \frac{1}{N} \sum _{n=1}^{N}W_{n}= \frac{1}{5} \left( 79.8+80+80.1+79.8+80.2 \right) = 79.98kg
W=N1n=1∑NWn=51(79.8+80+80.1+79.8+80.2)=79.98kg
上述估计值,就是体重的期望。
所谓期望,可以直观理解为对一个隐藏状态进行足够多次测量以后它所应表现出来的值(译注:这一段原文作者为了简单起见叙述并不是很好,简单理解为,我们无法知道随机变量的真值,只能进行测量,测量得到的样本含有随机性,服从某个分布,我们可以依照分布对样本求概率加权平均,当样本数趋于无穷大时的概率加权平均值的极限就是该随机变量真值的期望。即平均值与样本对应,期望与随机变量对应,样本是我们能看到的,真值我们看不到,二者之间的桥梁就是样本数趋于无穷大)。
均值通常使用希腊字母 μ 来表示。
字母 E 通常表示期望。
方差和标准差
方差 Variance是对数据样本在其均值附近散布情况进行的度量,标准差 Standard Deviation是方差的平方根。
标准差通常用希腊字母 σ \sigma σ. 对应地,方差即为 σ 2 \sigma^{2} σ2.
现在假设我们想比较两个高中篮球队的身高分布情况,下表给出了两支球队球员的身高,以及每支球队身高的均值。
球员 1 球员 2 球员 3 球员 4 球员 5 身高均值
球队 A 1.89m 2.1m 1.75m 1.98m 1.85m 1.914m
球队 B 1.94m 1.9m 1.97m 1.89m 1.87m 1.914m
可见,两支球队的身高均值是相同的。我们再来看它们的方差。
由于方差度量的是数据样本的散布情况,我们需要计算每个样本到均值的离散程度。这可以通过将均值从每个样本中减去来实现。
身高记为 x x x,身高的均值记为 μ \mu μ. 样本到均值的差即为:
x
n
−
μ
=
x
n
−
1.914
m
x_{n} - \mu = x_{n}-1.914m
xn−μ=xn−1.914m
下表列出每个球员身高到平均值的差异。
球员 1 球员 2 球员 3 球员 4 球员 5
球队 A -0.024m 0.186m -0.164m 0.066m -0.064m
球队 B 0.026m -0.014m 0.056m -0.024m -0.044m
有些值是负数,而数据散布的度量应是无符号的。可以对这些值求平方来消除负数(译注:求绝对值也能消除负数,但绝对值不可导,并且散布度量一般希望强调散布更远的样本,平方能够自加权):
(
x
n
−
μ
)
2
=
(
x
n
−
1.914
m
)
2
\left( x_{n}- \mu \right) ^{2} = \left( x_{n}- 1.914m \right) ^{2}
(xn−μ)2=(xn−1.914m)2
下表列出每个球员身高到平均值的差异平方。
球员 1 球员 2 球员 3 球员 4 球员 5
球队 A 0.000576m2 0.034596m2 0.026896m2 0.004356m2 0.004096m2
球队 B 0.000676m2 0.000196m2 0.003136m2 0.000576m2 0.001936m2
接下来对这些平方值再求平均来得到方差:
σ
2
=
1
N
∑
n
=
1
N
(
x
n
−
μ
)
2
\sigma ^{2}= \frac{1}{N} \sum _{n=1}^{N} \left( x_{n}- \mu \right) ^{2}
σ2=N1n=1∑N(xn−μ)2
对球队A,身高方差为:
σ
A
2
=
1
N
∑
n
=
1
N
(
x
n
−
μ
)
2
=
1
5
(
0.000576
+
0.034596
+
0.026896
+
0.004356
+
0.004096
)
=
0.014
m
2
\sigma _{A}^{2} = \frac{1}{N} \sum _{n=1}^{N} \left( x_{n}- \mu \right) ^{2}= \frac{1}{5} \left( 0.000576+ 0.034596+ 0.026896+ 0.004356+ 0.004096 \right) = 0.014m^{2}
σA2=N1n=1∑N(xn−μ)2=51(0.000576+0.034596+0.026896+0.004356+0.004096)=0.014m2
对球队B,身高方差为:
σ
B
2
=
1
N
∑
n
=
1
N
(
x
n
−
μ
)
2
=
1
5
(
0.000676
+
0.000196
+
0.003136
+
0.000576
+
0.001936
)
=
0.0013
m
2
\sigma _{B}^{2} = \frac{1}{N} \sum _{n=1}^{N} \left( x_{n}- \mu \right) ^{2}= \frac{1}{5} \left( 0.000676+ 0.000196+ 0.003136+ 0.000576+ 0.001936 \right) = 0.0013m^{2}
σB2=N1n=1∑N(xn−μ)2=51(0.000676+0.000196+0.003136+0.000576+0.001936)=0.0013m2
可见,尽管两支球队的身高均值是相同的,球队A的身高散布要比球队B大。因此球队A的球员身高多样性要比球队B高。一支球队有多个不同的位置,例如控球后卫、得分后卫和中锋等,球队B身高分布过于集中,因而不便应对不同的位置带来的差异化要求。
本例中方差的量纲是米平方。通常用标准差更方便,因为标准差是方差的平方根,因此标准差的量纲和样本一致。
σ
=
1
N
∑
n
=
1
N
(
x
n
−
μ
)
2
\sigma =\sqrt[]{\frac{1}{N} \sum _{n=1}^{N} \left( x_{n}- \mu \right) ^{2}}
σ=N1n=1∑N(xn−μ)2
球队A球员身高的标准差是0.12m.
球队A球员身高的标准差是0.036m.
现在,再假设我们想求取全国所有高中篮球队队员身高的均值和方差。这是个海量工作量的任务 - 需要收集每一所高中的每一个球员的身高数据。
另一方面,我们也可以通过收集部分样本(一个量足够大的样本集),根据这个样本集对全国所有高中篮球队队员身高的均值和方差进行估计。
一个有100个随机选择出的球员的身高数据的样本集已经可以提供足够准确的估计了。
但是,从部分样本对真实方差进行估计的方程和从全量样本进行方差计算的方程略有不同。求和后的归一化系数是 N − 1 N-1 N−1而并非 N N N:
σ
2
=
1
N
−
1
∑
n
=
1
N
(
x
n
−
μ
)
2
\sigma ^{2}= \frac{1}{N-1} \sum _{n=1}^{N} \left( x_{n}- \mu \right) ^{2}
σ2=N−11n=1∑N(xn−μ)2
这个
1
N
−
1
\frac{1}{N-1}
N−11系数称为贝塞尔校正。
在visiondummy 和 Wikipedia上能看到这个矫正的数学证明和推导。
正态分布
自然界许多现象都遵循 正态分布 Normal Distribution。正态分布又称为 高斯分布 Gaussian Distribution (纪念著名数学家卡尔·弗莱德利希·高斯),其表达式如下:
f
(
x
;
μ
,
σ
2
)
=
1
2
π
σ
2
e
−
(
x
−
μ
)
2
2
σ
2
f \left( x; \mu , \sigma ^{2} \right) = \frac{1}{\sqrt[]{2 \pi \sigma ^{2}}}e^{\frac{- \left( x- \mu \right) ^{2}}{2 \sigma ^{2}}}
f(x;μ,σ2)=2πσ21e2σ2−(x−μ)2
其函数图像(高斯曲线)又被称为正态分布的 概率密度函数(PDF)。
下表描述了三个不同城市A、B和C里披萨外卖送达时间的概率密度函数。
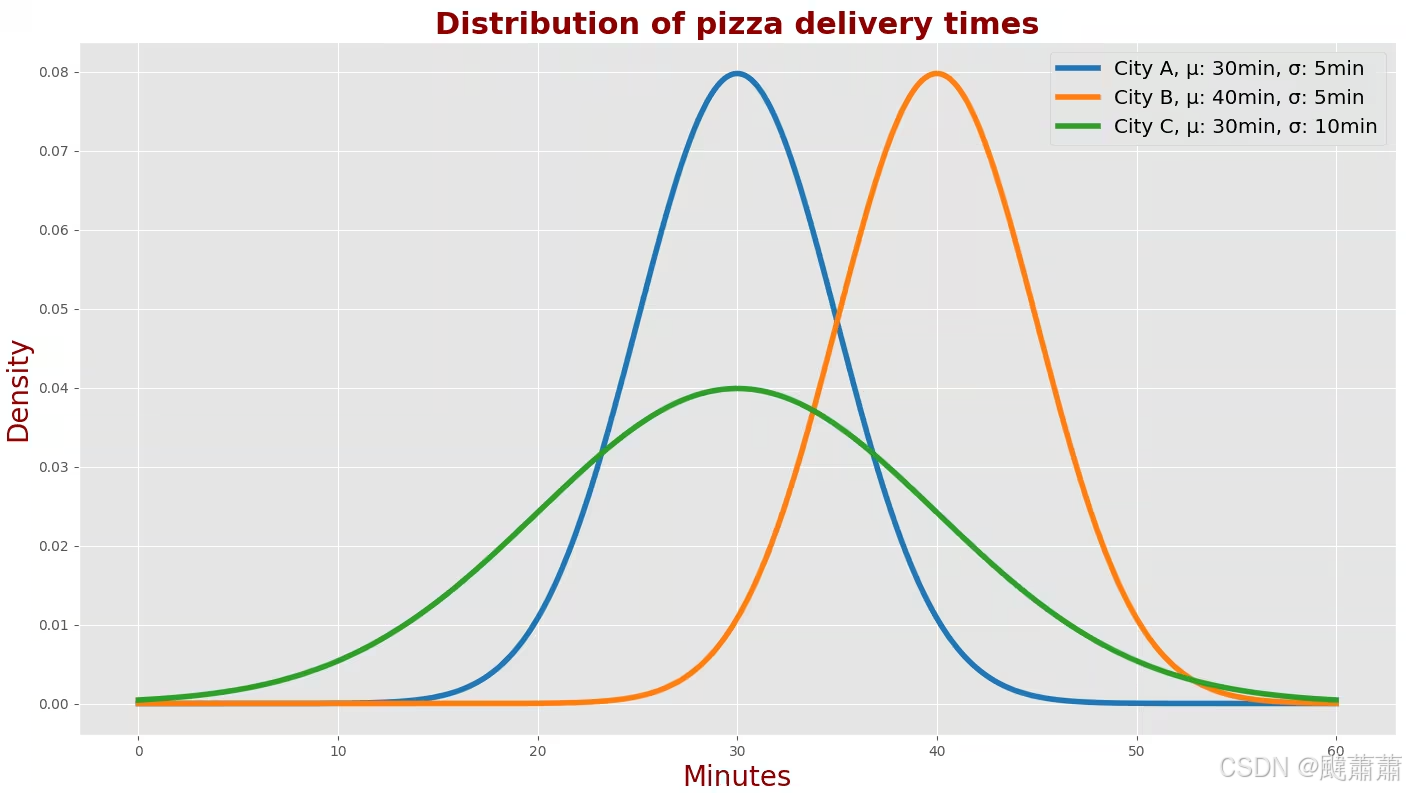
在A城,平均送达时间为30分钟,标准差为5分钟。
在B城,平均送达时间为40分钟,标准差为5分钟。
在C城,平均送达时间为30分钟,标准差为10分钟。
可以看到A城和B城的高斯曲线的形状是一样的,但是其中心对称轴位置不同。这表明在A城点披萨比在B城要平均少等待10分钟,但两座城市里送达时间的散布是差不多的。
还可以看到A城和C城的高斯曲线中心对称轴位置相同,但是形状不同。因此尽管平均送达时间一样,但散布不同。
下表列出了正态分布的曲线围成面积的比例情况:
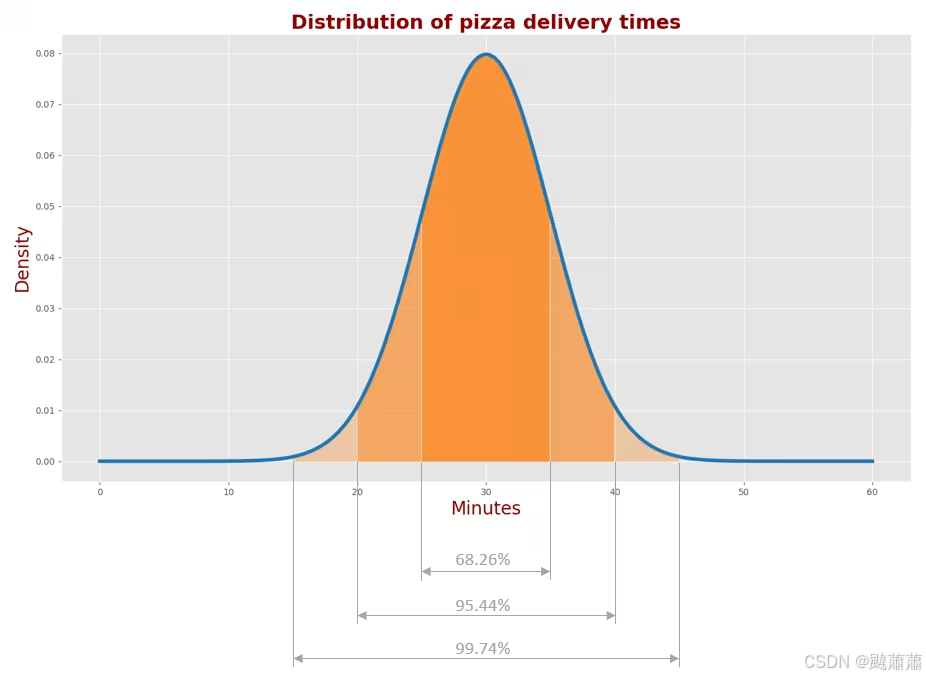
A城里68.26%的送达时间落在
μ
±
σ
\mu \pm \sigma
μ±σ 区间内(25-35分钟)
A城里95.44%的送达时间落在
μ
±
2
σ
\mu \pm 2\sigma
μ±2σ 区间内(20-40分钟)
A城里99.74%的送达时间落在
μ
±
3
σ
\mu \pm 3\sigma
μ±3σ 区间内(15-45分钟)
通常情况下,测量误差是正态分布的。卡尔曼滤波器假设测量误差具有正态分布。
随机变量
一个 随机变量 Random Variable 可以用来描述系统的隐藏状态。随机变量是一个集合,包含对应的随机试验所有可能的结果取值。
随机变量可以是连续的也可以是离散的:
- 连续随机变量可以在一个给定范围内取任何值,例如电池充电时间或者马拉松比赛时间。
- 离散随机变量是可数的,例如网站访问人数或者班里学生的数量。
随机变量使用概率密度函数描述,概率密度函数具有一个特性,称为 矩 Moment,矩是随机变量幂的期望。我们重点关注两种矩:
- k k k 阶原点矩,是随机变量 k k k 次幂的期望: E ( X k ) E\left( X^{k} \right) E(Xk).
- k k k 阶中心距,是随机变量关于均值的散布的 k k k 次幂的期望: E ( ( X − μ X ) k ) E\left( \left( X - \mu_{X} \right)^{k} \right) E((X−μX)k).
本教程中,随机变量由下述两种矩进行描述:
- 一阶原点矩 E ( X ) E\left( X \right) E(X) - 测量结果的均值。
- 二阶中心矩 E ( ( X − μ X ) 2 ) E\left( \left( X - \mu_{X} \right)^{2} \right) E((X−μX)2) - 测量结果的方差。
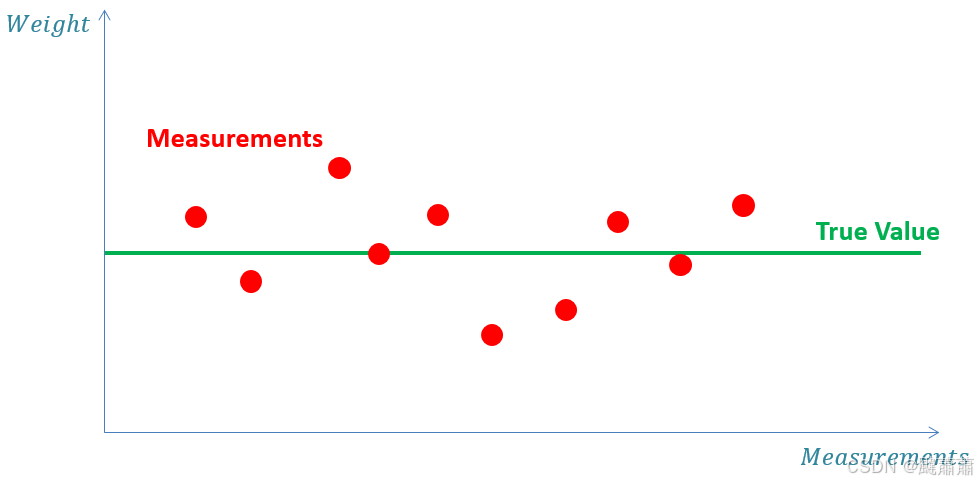
估计,准度和精度
所谓 估计 Estimation 是对系统的隐藏状态的估计。例如某飞行器的真实位置对观测者而言是不可见的,我们可以用传感器,例如雷达,来估计飞行器的位置。通过使用多个传感器并且使用先进的估计和跟踪算法(例如卡尔曼滤波)能够大幅提升对飞行器位置估计的效果。每次这样的测量和计算都是一次估计。
准度 Accuracy 描述测量值与真值的接近情况。
精度 Precision 描述一系列测量值相对同一个真值的偏差分布情况。
准度和精度是衡量一个估计的最基础和重要的指标。下图展示了准度和精度的区别:
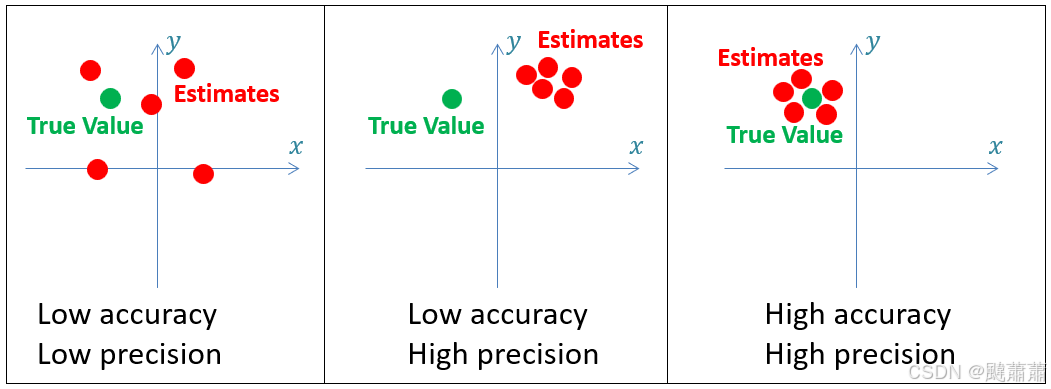
高精度系统的测量值具有很低的方差(即低不确定性),而低精度系统具有高方差(即高不确定性)。随机测量噪声造成了这些不确定性。
低准度系统又被称为 有偏 Biased 系统,源自它们的测量结果往往受系统性误差(偏差)的影响。
散布对测量的影响可以通过对测量结果求平均或进行平滑来降低。比如,用温度计测量的室内温度会包含随机测量噪声,我们可以测量多次然后取平均。因为误差是随机的,有些测量会比真值大,有些测量会比真值小,二者在求平均中抵消后平均结果会更接近真值。进行这样的测量越多,求得的估计值就越准确。
另一方面,一个有偏的温度计的测量结果经过上述估计后,仍然是有偏的。
本教程中所有的示例均假定测量系统是 无偏 Unbiased 的。
小结
下图从统计学角度展示了测量的过程。
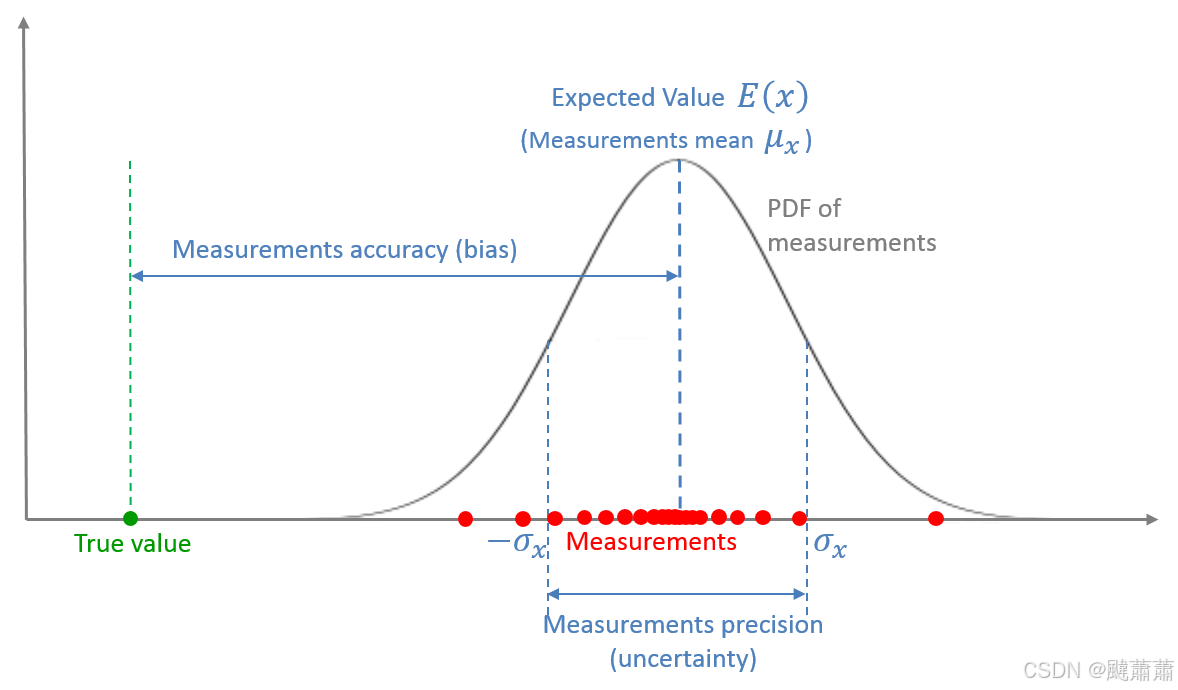
一次测量是对一个随机变量的取样,该随机变量由一个 概率密度函数 (PDF)来描述。
多次测量的平均值就是该随机变量的 期望。
均值和真值之间的差是该测量系统的 偏差 或者 系统性误差,它构成了测量系统的 准度。
测量值的散布程度是该测量系统的 测量噪声,又叫 随机测量误差 或 测量不确定性,它构成了测量系统的 精度。
α − β − γ \alpha-\beta-\gamma α−β−γ滤波器
示例 1 – 给金条称重
现在介绍第一个简单示例。本例对一个静态系统的状态进行估计。所谓静态系统,是指在合理时间范围内系统状态不会自发改变的系统。例如一座塔便是一个静态系统,高度便是其状态之一,它不随时间改变而变化。
本例中,我们估计一根金条的重量。假定我们用来称金条的秤是无偏的,即称重结果没有系统性偏差,但是有随机噪声。
金条就是我们所关心的系统,金条的重量就是该系统的状态。该系统的动态模型是恒定的,因为我们假定金条的重量(在短时间内)不会发生变化。
为了估计出该系统的状态(金条重量),我们可以对其进行多次称重,然后取多次测量结果的平均值。
在时刻
n
n
n,估计值
x
^
n
,
n
\hat{x}_{n,n}
x^n,n 便是所有之前测量的平均值:
x
^
n
,
n
=
1
n
(
z
1
+
z
2
+
…
+
z
n
−
1
+
z
n
)
=
1
n
∑
i
=
1
n
(
z
i
)
\hat{x}_{n,n}= \frac{1}{n} \left( z_{1}+ z_{2}+ \ldots + z_{n-1}+ z_{n} \right) = \frac{1}{n} \sum _{i=1}^{n} \left( z_{i} \right)
x^n,n=n1(z1+z2+…+zn−1+zn)=n1i=1∑n(zi)
注解:
x
x
x 是金条重量的真值
z
n
z_{n}
zn 是
n
n
n 时刻对金条重量的测量值
x
^
n
,
n
\hat{x}_{n,n}
x^n,n 是在
n
n
n 时刻,使用了
n
n
n 时刻的测量值
z
n
z_{n}
zn,对
x
x
x 的估计值
x
^
n
+
1
,
n
\hat{x}_{n+1,n}
x^n+1,n 是在
n
n
n 时刻对未来状态(
n
+
1
n+1
n+1 时刻)的预测,记为
x
^
n
+
1
,
n
\hat{x}_{n+1,n}
x^n+1,n ,或者说外插
x
^
n
−
1
,
n
−
1
\hat{x}_{n-1,n-1}
x^n−1,n−1 是在
n
−
1
n-1
n−1 时刻,使用了
n
−
1
n-1
n−1 时刻的测量值
z
n
−
1
z_{n-1}
zn−1,对
x
x
x 的估计值
x
^
n
,
n
−
1
\hat{x}_{n,n-1}
x^n,n−1 是一个先验估计 - 在
n
−
1
n-1
n−1 时刻对
n
n
n 时刻的系统状态所进行的预测(译注:对第n个时刻而言,
x
^
n
,
n
−
1
\hat{x}_{n,n-1}
x^n,n−1 是先验估计,
x
^
n
+
1
,
n
\hat{x}_{n+1,n}
x^n+1,n 是预测)
注:在本教程中,变量上的尖号符号(或者叫hat)代表这是一个对该变量的估计值。
由于金条的重量不随时间改变而改变,系统动态模型在本例中是静态的(恒定),因此有
x
^
n
+
1
,
n
=
x
^
n
,
n
\hat{x}_{n+1,n}= \hat{x}_{n,n}
x^n+1,n=x^n,n .
上面求平均的表达式虽然在数学层面是正确的,但是它不具备可实现性。这是因为根据平均值的定义,为了估计 x ^ n , n \hat{x}_{n,n} x^n,n ,我们需要存储下所有的历史测量值,这对内存开销巨大。并且每次获得了新的测量值后都需要完全重新从第一次测量开始计算,这对CPU算力也消耗巨大。
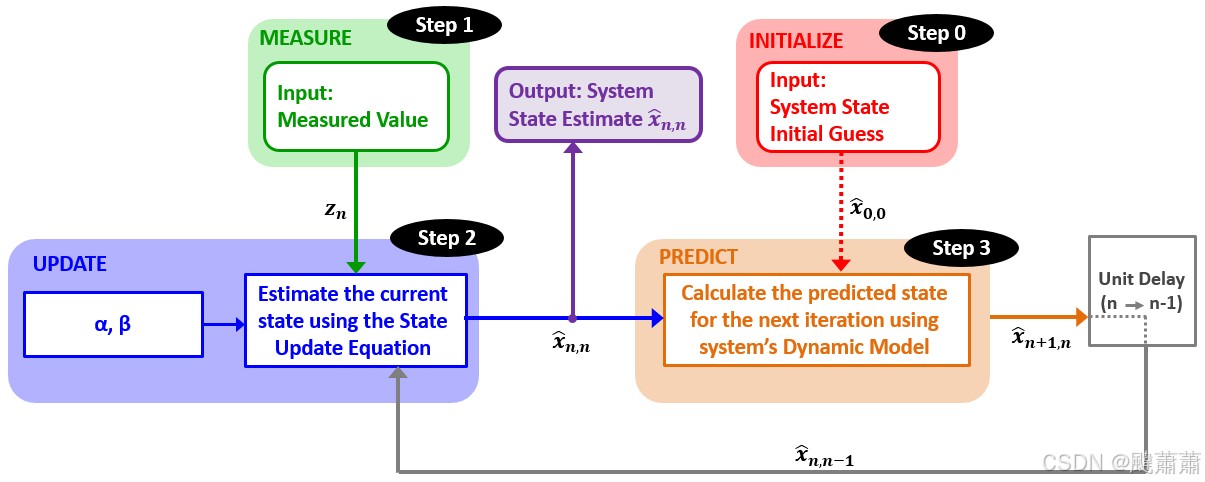
现实一点的考虑是,最好只需存储上一时刻的估计值 x ^ n − 1 , n − 1 \hat{x}_{n-1,n-1} x^n−1,n−1 ,并在新的测量完成后更新它即可。下图描述了这个思路:
根据当前的测量和先验估计,估计当前的状态。
根据当前的状态估计以及系统动态模型,进行下一时刻的预测。
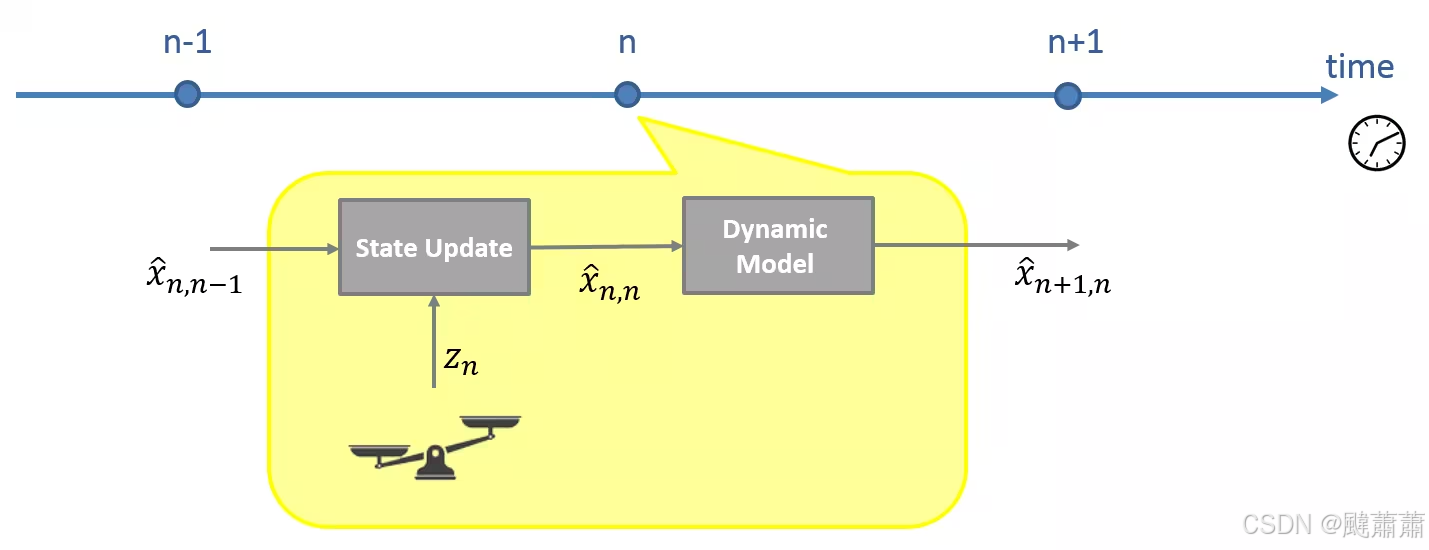
把上述求平均的表达式在数学上等效变换一下,可以得到:
| 表达式 | 注解 |
|---|---|
| x ^ n , n = 1 n ∑ i = 1 n ( z i ) \hat{x}_{n,n}= \frac{1}{n} \sum _{i=1}^{n} \left( z_{i} \right) x^n,n=n1∑i=1n(zi) | 求平均公式: n n n 个测量的和再除以 n n n |
| = 1 n ( ∑ i = 1 n − 1 ( z i ) + z n ) = \frac{1}{n} \left( \sum _{i=1}^{n-1} \left( z_{i} \right) + z_{n} \right) =n1(∑i=1n−1(zi)+zn) | 前 n − 1 n - 1 n−1 个测量的和再加上最近一次的测量值整体除以 n n n |
| = 1 n ∑ i = 1 n − 1 ( z i ) + 1 n z n = \frac{1}{n} \sum _{i=1}^{n-1} \left( z_{i} \right) + \frac{1}{n} z_{n} =n1∑i=1n−1(zi)+n1zn | 1 n \frac{1}{n} n1 乘进去展开 |
| = 1 n n − 1 n − 1 ∑ i = 1 n − 1 ( z i ) + 1 n z n = \frac{1}{n}\frac{n-1}{n-1} \sum _{i=1}^{n-1} \left( z_{i} \right) + \frac{1}{n} z_{n} =n1n−1n−1∑i=1n−1(zi)+n1zn | 给求和项同时乘以并除以 n − 1 n - 1 n−1 |
| = n − 1 n 1 n − 1 ∑ i = 1 n − 1 ( z i ) + 1 n z n = \frac{n-1}{n}\color{#FF8C00}{\frac{1}{n-1} \sum _{i=1}^{n-1} \left( z_{i} \right)} + \frac{1}{n} z_{n} =nn−1n−11∑i=1n−1(zi)+n1zn | 调整顺序, 橘黄色的项就是上一时刻的估计值 |
| = n − 1 n x ^ n − 1 , n − 1 + 1 n z n = \frac{n-1}{n}\color{#FF8C00}{\hat{x}_{n-1,n-1}} + \frac{1}{n} z_{n} =nn−1x^n−1,n−1+n1zn | 把求和项用上一时刻的估计值替换掉 |
| = x ^ n − 1 , n − 1 − 1 n x ^ n − 1 , n − 1 + 1 n z n = \hat{x}_{n-1,n-1}- \frac{1}{n}\hat{x}_{n-1,n-1}+ \frac{1}{n} z_{n} =x^n−1,n−1−n1x^n−1,n−1+n1zn | 把 (\hat{x}_{n-1,n-1}) 乘进 n − 1 n \frac{n-1}{n} nn−1 的分子,并拆项 |
| = x ^ n − 1 , n − 1 + 1 n ( z n − x ^ n − 1 , n − 1 ) = \hat{x}_{n-1,n-1}+ \frac{1}{n} \left( z_{n}- \hat{x}_{n-1,n-1} \right) =x^n−1,n−1+n1(zn−x^n−1,n−1) | 提出 1 n \frac{1}{n} n1, x ^ n − 1 , n − 1 \hat{x}_{n-1,n-1} x^n−1,n−1 就是在 n − 1 n - 1 n−1 时刻使用 n − 1 n-1 n−1 时刻的测量值对 x x x 的状态估计。 |
接下来使用 n − 1 n-1 n−1 时刻的估计值 x ^ n − 1 , n − 1 \hat{x}_{n-1,n-1} x^n−1,n−1 计算 x ^ n , n − 1 \hat{x}_{n,n-1} x^n,n−1 (对 n n n 时刻 x x x 的预测)。即把 x ^ n − 1 , n − 1 \hat{x}_{n-1,n-1} x^n−1,n−1 外插至 n n n 时刻。
由于系统模型是静态的,当前时刻对 x x x 的预测就等于上一时刻对 x x x 的估计: x ^ n , n − 1 = x ^ n − 1 , n − 1 \hat{x}_{n,n-1} = \hat{x}_{n-1,n-1} x^n,n−1=x^n−1,n−1.
基于上述推导,对当前时刻状态 x ^ n , n \hat{x}_{n,n} x^n,n 的估计可以写成:
x
^
n
,
n
=
x
^
n
,
n
−
1
+
1
n
(
z
n
−
x
^
n
,
n
−
1
)
\hat{x}_{n,n} = \hat{x}_{n,n-1} + \frac{1}{n} \left( z_{n} - \hat{x}_{n,n-1} \right)
x^n,n=x^n,n−1+n1(zn−x^n,n−1)
上式即为卡尔曼滤波的五个方程之一。称为状态更新方程。其意为:

系数
1
n
\frac{1}{n}
n1 是本例特定的。后面会具体谈到这个系数的重要性,但此刻可以先指出,在卡尔曼滤波的语境中,这个系数被称作卡尔曼增益,符号为
K
n
K_{n}
Kn. 其具有下标
n
n
n 意味着卡尔曼增益随着每次迭代都会改变。
K n K_{n} Kn 的提出是Rudolf Kalman重要的贡献之一。
在进展到卡尔曼滤波之前,我们先不用 K n K_{n} Kn,而是用希腊字母 α n \alpha _{n} αn 来表示这个系数。
所以状态更新方程可以写作:
x
^
n
,
n
=
x
^
n
,
n
−
1
+
α
n
(
z
n
−
x
^
n
,
n
−
1
)
\hat{x}_{n,n}= \hat{x}_{n,n-1}+ \alpha _{n} \left( z_{n}-\hat{x}_{n,n-1} \right)
x^n,n=x^n,n−1+αn(zn−x^n,n−1)
(
z
n
−
x
^
n
,
n
−
1
)
\left( z_{n}- \hat{x}_{n,n-1} \right)
(zn−x^n,n−1) 这一项被称为“测量残差”,也叫更新量。更新量包含新的信息。
本例中,随着 n n n 的增加, 1 n \frac{1}{n} n1 会下降。在一开始,因为没有足够的信息,第一次估计完全是基于第一次的测量值的( 1 n ∣ n = 1 = 1 \frac{1}{n}|_{n=1} = 1 n1∣n=1=1)。随着迭代进行,每次后续测量的权重都在下降,并且会逐渐变得可以忽略不计。
继续讲示例。在进行第一次测量之前,我们可以根据金条上的钢印来猜测(或粗略估计)金条的重量,这是 初始估计,是算法的第一个估计值。
卡尔曼滤波需要一个初始估计作为初始值,这个值可以非常粗略。
估计算法
下图描述了本例中所使用的算法。
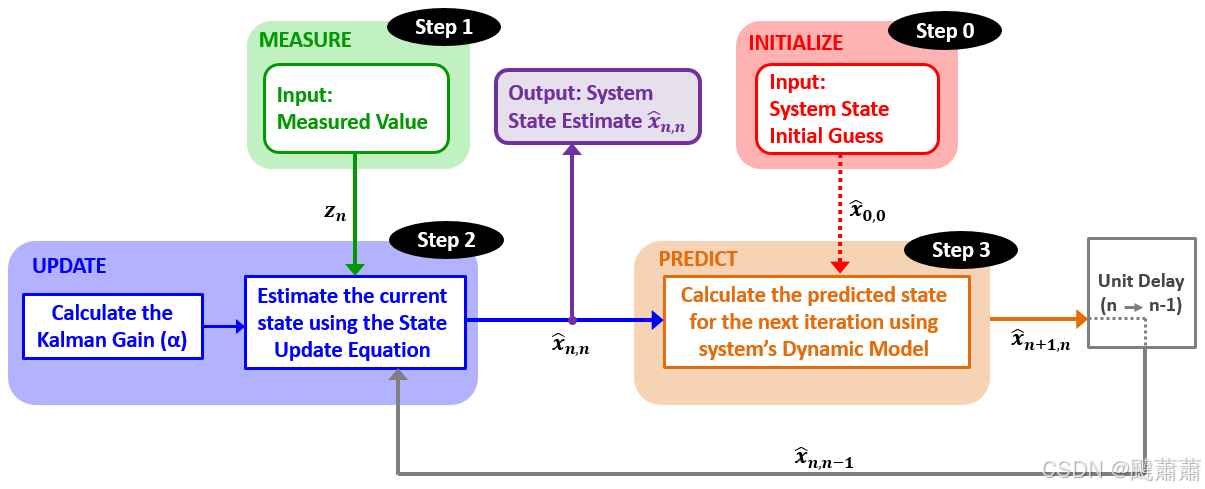
现在,可以开始具体测量和估计的过程了。
数值示例
- 第0次迭代
初始化
金条重量的初始估计是1000g,这个估计仅在滤波器初始化时使用一次,后续迭代不再需要这个值。
x ^ 0 , 0 = 1000 g \hat{x}_{0,0}=1000g x^0,0=1000g
预测
金条的重量不会改变,系统模型是静态的,下一个时刻的预测就等于此时的初始化估计值。
x ^ 1 , 0 = x ^ 0 , 0 = 1000 g \hat{x}_{1,0} = \hat{x}_{0,0}=1000g x^1,0=x^0,0=1000g
- 第1次迭代
第1步
用秤称重:
z 1 = 996 g z_{1}= 996g z1=996g
第2步
计算增益。本例中
α
n
=
1
n
\alpha_{n}= \frac{1}{n}
αn=n1,故:
α 1 = 1 1 = 1 \alpha_{1}= \frac{1}{1}=1 α1=11=1
用状态更新方程计算当前的估计值:
x ^ 1 , 1 = x ^ 1 , 0 + α 1 ( z 1 − x ^ 1 , 0 ) = 1000 + 1 ( 996 − 1000 ) = 996 g \hat{x}_{1,1}= \hat{x}_{1,0}+ \alpha _{1} \left( z_{1}- \hat{x}_{1,0} \right) = 1000+1 \left( 996-1000 \right) = 996g x^1,1=x^1,0+α1(z1−x^1,0)=1000+1(996−1000)=996g
注:初始估计可以是任何值,由于
α
1
=
1
\alpha _{1}= 1
α1=1,初始值在第1次迭代的时候将被抵消。
第3步
系统模型是静态的,金条的重量不应该改变,下一时刻的预测应该等于此时的估计:
x ^ 2 , 1 = x ^ 1 , 1 = 996 g \hat{x}_{2,1}= \hat{x}_{1,1}=996g x^2,1=x^1,1=996g
- 第2次迭代
在一个采样周期过后,上一时刻的预测值成为了这一时刻的先验估计。
x ^ 2 , 1 = 996 g \hat{x}_{2,1}=996g x^2,1=996g
第1步
做第二次称重:
z 2 = 994 g z_{2}= 994g z2=994g
第2步
计算增益:
α 2 = 1 2 \alpha _{2}= \frac{1}{2} α2=21
计算估计值:
x ^ 2 , 2 = x ^ 2 , 1 + α 2 ( z 2 − x ^ 2 , 1 ) = 996 + 1 2 ( 994 − 996 ) = 995 g \hat{x}_{2,2}= \hat{x}_{2,1}+ \alpha_{2} \left( z_{2}- \hat{x}_{2,1} \right) =996+\frac{1}{2} \left( 994-996 \right) = 995g x^2,2=x^2,1+α2(z2−x^2,1)=996+21(994−996)=995g
第3步
x
^
3
,
2
=
x
^
2
,
2
=
995
g
\hat{x}_{3,2}= \hat{x}_{2,2}=995g
x^3,2=x^2,2=995g
- 第3次迭代
z 3 = 1021 g α 3 = 1 3 z_{3}= 1021g~~~~~~~~~~~~~~~~~~~~~~~~~~ \alpha_{3}= \frac{1}{3} z3=1021g α3=31 x ^ 3 , 3 = 995 + 1 3 ( 1021 − 995 ) = 1003.67 g \hat{x}_{3,3}=~ 995+\frac{1}{3} \left( 1021-995 \right) =1003.67g x^3,3= 995+31(1021−995)=1003.67g x ^ 4 , 3 = 1003.67 g \hat{x}_{4,3}=1003.67g x^4,3=1003.67g
-
第4次迭代
z 4 = 1000 g α 4 = 1 4 z_{4}= 1000g~~~~~~~~~~~~~~~~~~~~~~~~~~ \alpha_{4}= \frac{1}{4} z4=1000g α4=41 x ^ 4 , 4 = 1003.67 + 1 4 ( 1000 − 1003.67 ) = 1002.75 g \hat{x}_{4,4}= 1003.67+\frac{1}{4} \left( 1000-1003.67 \right) =1002.75g x^4,4=1003.67+41(1000−1003.67)=1002.75g x ^ 5 , 4 = 1002.75 g \hat{x}_{5,4}=1002.75g x^5,4=1002.75g -
第5次迭代
z 5 = 1002 g α 5 = 1 5 z_{5}= 1002g~~~~~~~~~~~~~~~~~~~~~~~~~~ \alpha_{5}= \frac{1}{5} z5=1002g α5=51 x ^ 5 , 5 = 1002.75 + 1 5 ( 1002 − 1002.75 ) = 1002.6 g \hat{x}_{5,5}= 1002.75+\frac{1}{5} \left( 1002-1002.75 \right) =1002.6g x^5,5=1002.75+51(1002−1002.75)=1002.6g x ^ 6 , 5 = 1002.6 g \hat{x}_{6,5}=1002.6g x^6,5=1002.6g -
第6次迭代
z 6 = 1010 g α 6 = 1 6 z_{6}= 1010g~~~~~~~~~~~~~~~~~~~~~~~~~~ \alpha_{6}= \frac{1}{6} z6=1010g α6=61 x ^ 6 , 6 = 1002.6 + 1 6 ( 1010 − 1002.6 ) = 1003.83 \hat{x}_{6,6}= 1002.6+\frac{1}{6} \left( 1010-1002.6 \right) =1003.83 x^6,6=1002.6+61(1010−1002.6)=1003.83 x ^ 7 , 6 = 1003.83 g \hat{x}_{7,6}=1003.83g x^7,6=1003.83g -
第7次迭代
z 7 = 983 g α 7 = 1 7 z_{7}=983g~~~~~~~~~~~~~~~~~~~~~~~~~~ \alpha_{7}= \frac{1}{7} z7=983g α7=71 x ^ 7 , 7 = 1003.83 + 1 7 ( 983 − 1003.83 ) = 1000.86 g \hat{x}_{7,7}= 1003.83+\frac{1}{7} \left( 983-1003.83 \right) =1000.86g x^7,7=1003.83+71(983−1003.83)=1000.86g x ^ 8 , 7 = 1000.86 g \hat{x}_{8,7}=1000.86g x^8,7=1000.86g -
第8次迭代
z 8 = 971 g α 8 = 1 8 z_{8}=971g~~~~~~~~~~~~~~~~~~~~~~~~~~ \alpha_{8}= \frac{1}{8} z8=971g α8=81 x ^ 8 , 8 = 1000.86 + 1 8 ( 971 − 1000.86 ) = 997.125 g \hat{x}_{8,8}= 1000.86+\frac{1}{8} \left( 971-1000.86 \right) =997.125g x^8,8=1000.86+81(971−1000.86)=997.125g x ^ 9 , 8 = 997.125 g \hat{x}_{9,8}=997.125g x^9,8=997.125g -
第9次迭代
z 9 = 993 g α 9 = 1 9 z_{9}=993g~~~~~~~~~~~~~~~~~~~~~~~~~~ \alpha_{9}= \frac{1}{9} z9=993g α9=91 x ^ 9 , 9 = 997.125 + 1 9 ( 993 − 997.125 ) = 996.67 g \hat{x}_{9,9}= 997.125+\frac{1}{9} \left( 993-997.125 \right) =996.67g x^9,9=997.125+91(993−997.125)=996.67g x ^ 10 , 9 = 996.67 g \hat{x}_{10,9}=996.67g x^10,9=996.67g -
第10次迭代
z 10 = 1023 g α 10 = 1 10 z_{10}=1023g~~~~~~~~~~~~~~~~~~~~~~~~~~ \alpha_{10}= \frac{1}{10} z10=1023g α10=101 x ^ 10 , 10 = 996.67 + 1 10 ( 1023 − 996.67 ) = 999.3 g \hat{x}_{10,10}= 996.67+\frac{1}{10} \left( 1023-996.67 \right) =999.3g x^10,10=996.67+101(1023−996.67)=999.3g x ^ 11 , 10 = 999.3 g \hat{x}_{11,10}=999.3g x^11,10=999.3g
至此先告一段落。增益随着每次测量而减小,故后面的测量对估计值的贡献总小于前面的测量。我们已经很接近真实的金条重量了(1000g)。如果做更多次的称重,我们会和真值更加接近。
下表汇总并比较了上面的测量值、估计值以及真值。
| 变量 | 数值 |
|---|---|
| n n n | 1 2 3 4 5 6 7 8 9 10 |
| α n \alpha _{n} αn | 1 1 1 1 2 \frac{1}{2} 21 1 3 \frac{1}{3} 31 1 4 \frac{1}{4} 41 1 5 \frac{1}{5} 51 1 6 \frac{1}{6} 61 1 7 \frac{1}{7} 71 1 8 \frac{1}{8} 81 1 9 \frac{1}{9} 91 1 10 \frac{1}{10} 101 |
| z n z_{n} zn | 996 994 1021 1000 1002 1010 983 971 993 1023 |
| x ^ n , n \hat{x}_{n,n} x^n,n | 996 995 1003.67 1002.75 1002.6 1003.83 1000.86 997.125 996.67 999.3 |
| x ^ n + 1 , n \hat{x}_{n+1,n} x^n+1,n | 996 995 1003.67 1002.75 1002.6 1003.83 1000.86 997.125 996.67 999.3 |
结果分析
下图中列出了测量值、估计值以及真值。
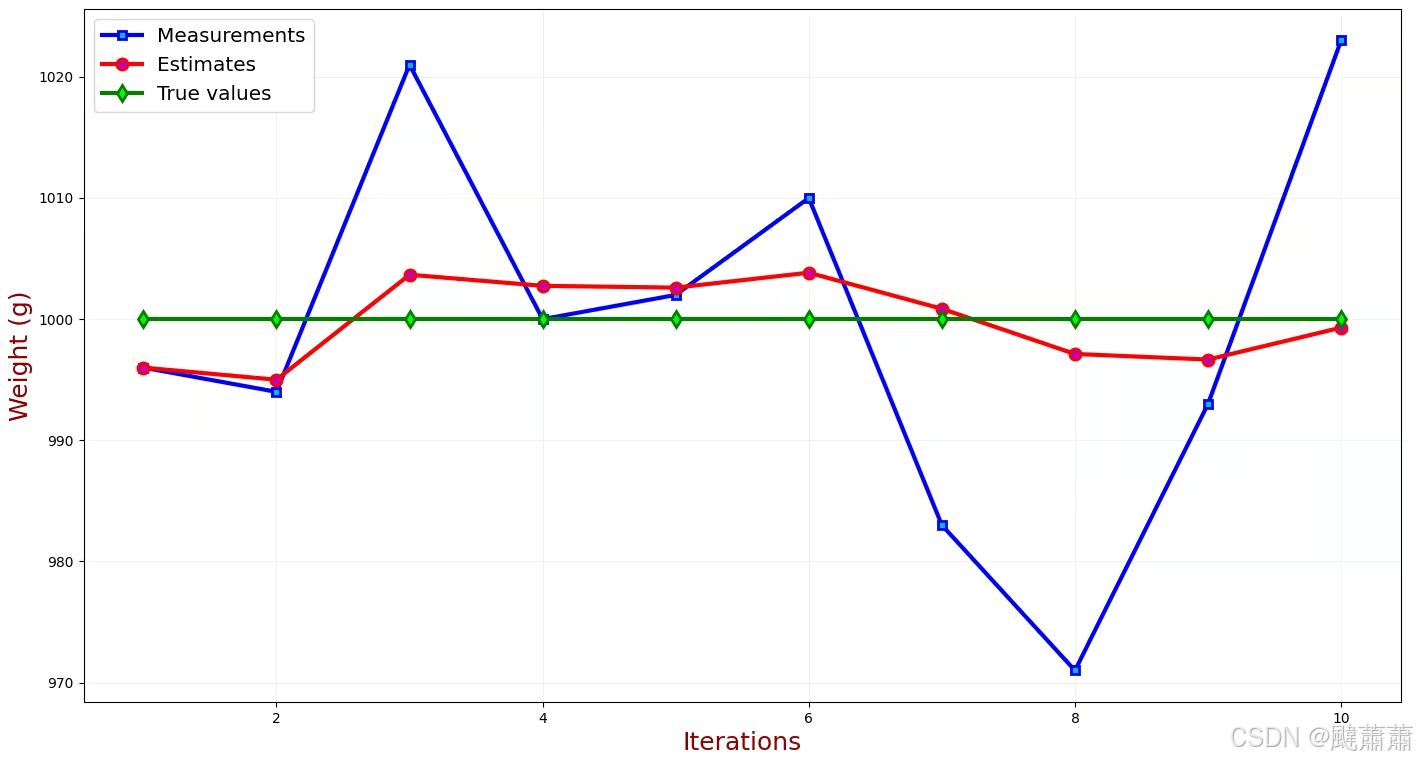
示例小结
本例中,我们设计了一个针对静态系统的简单估计算法。我们还推导出了五个卡尔曼滤波方程之一的状态更新方程。下一章中我们会重新审视这个状态更新方程。
示例 2 - 跟踪直线匀速运动的飞行器
是时候考虑一下状态随时间变化的动态系统了。本例中,我们尝试用 α − β \alpha - \beta α−β 滤波器 对一个直线匀速飞行中的飞行器进行跟踪。
假设一个只有一个维度的世界中,有这样一个飞行器在往远离雷达的方向飞行(或者靠近雷达)。因为是一维空间,飞行器到雷达的角度是恒定的,其高度也是恒定的。
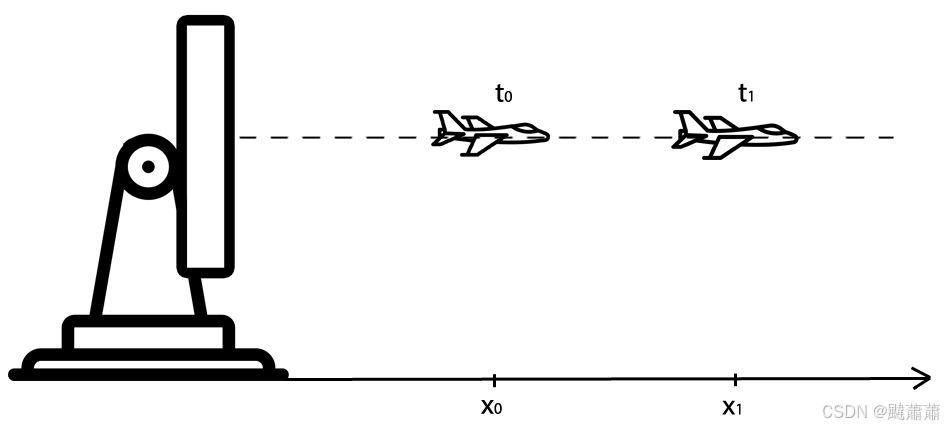
x
n
x_{n}
xn 表示
n
n
n 时刻飞行器的距离。飞行器速度可以近似用距离差分法得到 - 计算距离随时间的变化率。
因此,速度是距离的导数:
x
˙
=
v
=
d
x
d
t
\dot{x}= v= \frac{dx}{dt}
x˙=v=dtdx
雷达向目标的方向以固定频率发射跟踪波束,两次跟踪测量之间的时间间隔为
Δ
t
\Delta t
Δt.
则匀速运动的动力学模型可以由下面的运动方程给出:
x
n
+
1
=
x
n
+
Δ
t
x
˙
n
x_{n+1}= x_{n}+ \Delta t\dot{x}_{n}
xn+1=xn+Δtx˙n
x
˙
n
+
1
=
x
˙
n
\dot{x}_{n+1}= \dot{x}_{n}
x˙n+1=x˙n
根据这些方程,下一个采样周期时的飞行器距离等于当前飞行器距离加上目标速度乘以采样间隔时间。由于我们假设飞行器的速度不变,下一时刻的速度等于当前时刻的速度。
上述方程称为 状态外插方程 (也叫 转移方程 或 预测方程)。
在上个示例中我们已经用过状态外插方程了,只不过上个例子中这个方程是个恒等式,即下一时刻的状态等于当前时刻的状态。
状态外插方程依赖系统动态模型,因此不同的示例中这个方程也不同。
这个方程有一个以矩阵形式给出的更加一般的形式,后续会讲到。
上述方程的形式是本例特有的。
注:我们已经学到了两个卡尔曼滤波方程: 状态更新方程、 状态外插方程
现在我们来把状态更新方程改一改。
α − β \alpha - \beta α−β 滤波器
假设雷达的跟踪间隔 ( Δ t \Delta t Δt ) 为5秒,假设 n − 1 n - 1 n−1 时刻飞行器的距离为30,000m,其速度为40m/s.
使用上述状态外插方程,我们能够预测 n n n 时刻的目标位置为:
x ^ n , n − 1 = x ^ n − 1 , n − 1 + Δ t x ˙ ^ n − 1 , n − 1 = 30000 + 5 × 40 = 30200 m \hat{x}_{n,n-1}= \hat{x}_{n-1,n-1}+ \Delta t\hat{\dot{x}}_{n-1,n-1}=30000+5\times40=30200m x^n,n−1=x^n−1,n−1+Δtx˙^n−1,n−1=30000+5×40=30200m
预测目标 n n n 时刻的速度为:
x ˙ ^ n , n − 1 = x ˙ ^ n − 1 , n − 1 = 40 m / s \hat{\dot{x}}_{n,n-1}= \hat{\dot{x}}_{n-1,n-1}=40m/s x˙^n,n−1=x˙^n−1,n−1=40m/s
然而 n n n 时刻雷达测量的目标距离 ( z n z_{n} zn ) 为30,110m而非30,200m。预测和实际测量的距离之间相差了90m. 这个差有可能是两个原因导致的:
- 雷达测量不够精准
- 飞行器速度变化了。新的速度是
30
,
110
−
30
,
000
5
=
22
m
/
s
\frac{30,110-30,000}{5}=22m/s
530,110−30,000=22m/s
哪个原因是正确的呢?
我们把速度的状态更新方程写下来:
x
˙
^
n
,
n
=
x
˙
^
n
,
n
−
1
+
β
(
z
n
−
x
^
n
,
n
−
1
Δ
t
)
\hat{\dot{x}}_{n,n}= \hat{\dot{x}}_{n,n-1}+ \beta \left( \frac{z_{n}-\hat{x}_{n,n-1}}{ \Delta t} \right)
x˙^n,n=x˙^n,n−1+β(Δtzn−x^n,n−1)
系数
β
\beta
β 的值和雷达的测量精度等级有关。假设雷达的
1
σ
1 \sigma
1σ 精度是20m,那么90m的误差大概率是飞行器速度改变了,我们应该把
β
\beta
β 的值调高一些。如果
β
\beta
β 设为0.9,那么此时估计的速度就应该是:
x ˙ ^ n , n = x ˙ ^ n , n − 1 + β ( z n − x ^ n , n − 1 Δ t ) = 40 + 0.9 ( 30110 − 30200 5 ) = 23.8 m / s \hat{\dot{x}}_{n,n}= \hat{\dot{x}}_{n,n-1}+ \beta \left( \frac{z_{n}-\hat{x}_{n,n-1}}{ \Delta t} \right) =40+0.9 \left( \frac{30110-30200}{5} \right) =23.8m/s x˙^n,n=x˙^n,n−1+β(Δtzn−x^n,n−1)=40+0.9(530110−30200)=23.8m/s
而另一方面,假如雷达的 1 σ 1 \sigma 1σ 精度是150m,那90m的误差大概率是雷达测得不准,我们应该把 β \beta β 的值降低一些。如果 β \beta β 的值降为0.1,那么估计的速度就应该是:
x ˙ ^ n , n = x ˙ ^ n , n − 1 + β ( z n − x ^ n , n − 1 Δ t ) = 40 + 0.1 ( 30110 − 30200 5 ) = 38.2 m / s \hat{\dot{x}}_{n,n}= \hat{\dot{x}}_{n,n-1}+ \beta \left( \frac{z_{n}-\hat{x}_{n,n-1}}{ \Delta t} \right) =40+0.1 \left( \frac{30110-30200}{5} \right) =38.2m/s x˙^n,n=x˙^n,n−1+β(Δtzn−x^n,n−1)=40+0.1(530110−30200)=38.2m/s
如果是飞行器真实速度从40m/s降到了22m/s,可以看到在10个测量周期之后(把上面的公式以 β \beta β = 0.1 带入10次),飞行器速度的估计也逐渐降到了22m/s. 而如果是因为雷达测量不准,则后续测量的位置将会大致均匀散布在真实位置前后,整体上计算出来的平均速度会保持在40m/s左右不变。
飞行器位置的状态更新方程与上一个例子里的方程类似:
x
^
n
,
n
=
x
^
n
,
n
−
1
+
α
(
z
n
−
x
^
n
,
n
−
1
)
\hat{x}_{n,n}= \hat{x}_{n,n-1}+ \alpha \left( z_{n}- \hat{x}_{n,n-1} \right)
x^n,n=x^n,n−1+α(zn−x^n,n−1)
和上例不同的是,上例里
α
\alpha
α 系数每周期都在重新计算 (
α
n
=
1
n
\alpha _{n}= \frac{1}{n}
αn=n1 ),而本例中
α
\alpha
α 则是恒定的。
α \alpha α 系数的大小和雷达精度有关。对高精度雷达,应该选用高的 α \alpha α,以给测量值分配更高的权重。如果 α = 1 \alpha = 1 α=1,则估计的飞行器距离会等于测量值。
x ^ n , n = x ^ n , n − 1 + 1 ( z n − x ^ n , n − 1 ) = z n \hat{x}_{n,n}= \hat{x}_{n,n-1}+ 1 \left( z_{n}- \hat{x}_{n,n-1} \right) = z_{n} x^n,n=x^n,n−1+1(zn−x^n,n−1)=zn
如果 α = 0 \alpha =0 α=0,则测量值完全起不到任何作用:
x ^ n , n = x ^ n , n − 1 + 0 ( z n − x ^ n , n − 1 ) = x ^ n , n − 1 \hat{x}_{n,n} = \hat{x}_{n,n-1}+ 0 \left( z_{n}- \hat{x}_{n,n-1} \right) = \hat{x}_{n,n-1} x^n,n=x^n,n−1+0(zn−x^n,n−1)=x^n,n−1
于是我们推导出了雷达跟踪问题的状态更新方程。这又叫 α − β \alpha - \beta α−β 跟踪更新方程 或 α − β \alpha - \beta α−β 跟踪滤波方程。
位置的状态更新方程为:
x
^
n
,
n
=
x
^
n
,
n
−
1
+
α
(
z
n
−
x
^
n
,
n
−
1
)
\hat{x}_{n,n} = \hat{x}_{n,n-1}+ \alpha \left( z_{n}- \hat{x}_{n,n-1} \right)
x^n,n=x^n,n−1+α(zn−x^n,n−1)
速度的状态更新方程为:
x
˙
^
n
,
n
=
x
˙
^
n
,
n
−
1
+
β
(
z
n
−
x
^
n
,
n
−
1
Δ
t
)
\hat{\dot{x}}_{n,n} = \hat{\dot{x}}_{n,n-1}+ \beta \left( \frac{z_{n}-\hat{x}_{n,n-1}}{ \Delta t} \right)
x˙^n,n=x˙^n,n−1+β(Δtzn−x^n,n−1)
注:在其他的书中,
α
−
β
\alpha - \beta
α−β 滤波器又叫 g-h 滤波器,字母g代替了希腊字母
α
\alpha
α,字母h代替了希腊字母
β
\beta
β.
注:本例中,我们是根据雷达距离测量来间接估计的飞行器速度的 (
x
˙
=
Δ
x
Δ
t
\dot{x}= \frac{ \Delta x}{ \Delta t}
x˙=ΔtΔx ),实际上现代雷达可以直接用多普勒效应测量径向速度。但目前我们的目的是解释卡尔曼滤波而非雷达工作原理,所以为了简单起见,我们的示例中将全部用距离观测来间接测量速度。
估计算法
下图描述了本例所使用的估计算法。
与上一个示例不同,增益(
α
\alpha
α 和
β
\beta
β)的值在本例里是给定的。在卡尔曼滤波里,
α
\alpha
α 和
β
\beta
β 会被卡尔曼增益代替,并且每个采样周期会重新计算,后面会讲到。
现在来看一个数值示例。
数值示例
考虑一个在一维世界里正在向雷达靠近(或远离)的飞行器。
α − β \alpha - \beta α−β 滤波器的参数为:
α
=
0.2
\alpha =0.2
α=0.2.
β
=
0.1
\beta =0.1
β=0.1.
测量周期是5秒。
注:本例中,为了便于绘图,我们假设雷达是个低精度雷达,追踪的飞行器是架低速飞行器。现实中的雷达精度一般都更高,飞行器也更快。
- 第0次迭代
初始化
n
=
0
n=0
n=0 时刻的初始条件给定为:
x ^ 0 , 0 = 30000 m \hat{x}_{0,0}=30000m x^0,0=30000m x ˙ ^ 0 , 0 = 40 m / s \hat{\dot{x}}_{0,0}=40m/s x˙^0,0=40m/s
注:跟踪问题的初始化(或者说如何获得初始状态)是个十分重要的工作,后面会讲到。目前我们的目标是理解
α
−
β
\alpha - \beta
α−β 滤波器的基本原理,所以我们假设初始值已经合理获取了。
预测
初始值需要外插至第一个测量周期:
x ^ n + 1 , n = x ^ n , n + Δ t x ˙ ^ n , n → x ^ 1 , 0 = x ^ 0 , 0 + Δ t x ˙ ^ 0 , 0 = 30000 + 5 × 40 = 30200 m \hat{x}_{n+1,n}= \hat{x}_{n,n}+ \Delta t\hat{\dot{x}}_{n,n} \rightarrow \hat{x}_{1,0}= \hat{x}_{0,0}+ \Delta t\hat{\dot{x}}_{0,0} =30000+5 \times 40=30200m x^n+1,n=x^n,n+Δtx˙^n,n→x^1,0=x^0,0+Δtx˙^0,0=30000+5×40=30200m x ˙ ^ n + 1 , n = x ˙ ^ n , n → x ˙ ^ 1 , 0 = x ˙ ^ 0 , 0 = 40 m / s \hat{\dot{x}}_{n+1,n}= \hat{\dot{x}}_{n,n} \rightarrow \hat{\dot{x}}_{1,0}= \hat{\dot{x}}_{0,0} =40m/s x˙^n+1,n=x˙^n,n→x˙^1,0=x˙^0,0=40m/s
- 第1次迭代
第一个周期 ( n = 1 n=1 n=1 ),初始值就是先验估计:
x ^ n , n − 1 = x ^ 1 , 0 = 30200 m \hat{x}_{n,n-1} = \hat{x}_{1,0}=30200m x^n,n−1=x^1,0=30200m x ˙ ^ n , n − 1 = x ˙ ^ 1 , 0 = 40 m / s \hat{\dot{x}}_{n,n-1} = \hat{\dot{x}}_{1,0}=40m/s x˙^n,n−1=x˙^1,0=40m/s
第1步
雷达进行一次测距:
z 1 = 30171 m z_{1}= 30171m z1=30171m
第2步
用状态更新方程计算当前的状态估计:
x ^ 1 , 1 = x ^ 1 , 0 + α ( z 1 − x ^ 1 , 0 ) = 30200 + 0.2 ( 30171 − 30200 ) = 30194.2 m \hat{x}_{1,1} = \hat{x}_{1,0}+ \alpha \left( z_{1}- \hat{x}_{1,0} \right) =30200+0.2 \left( 30171-30200 \right) = 30194.2m x^1,1=x^1,0+α(z1−x^1,0)=30200+0.2(30171−30200)=30194.2m x ˙ ^ 1 , 1 = x ˙ ^ 1 , 0 + β ( z 1 − x ^ 1 , 0 Δ t ) = 40 + 0.1 ( 30171 − 30200 5 ) = 39.42 m / s \hat{\dot{x}}_{1,1}= \hat{\dot{x}}_{1,0}+ \beta \left( \frac{z_{1}-\hat{x}_{1,0}}{ \Delta t} \right) = 40+0.1 \left( \frac{30171-30200}{5} \right) = 39.42m/s x˙^1,1=x˙^1,0+β(Δtz1−x^1,0)=40+0.1(530171−30200)=39.42m/s
第3步
用状态外插方程预测下一周期的状态:
x ^ 2 , 1 = x ^ 1 , 1 + Δ t x ˙ ^ 1 , 1 = 30194.2 + 5 × 39.42 = 30391.3 m \hat{x}_{2,1}= \hat{x}_{1,1}+ \Delta t\hat{\dot{x}}_{1,1} =30194.2+5 \times 39.42=30391.3m x^2,1=x^1,1+Δtx˙^1,1=30194.2+5×39.42=30391.3m x ˙ ^ 2 , 1 = x ˙ ^ 1 , 1 = 39.42 m / s \hat{\dot{x}}_{2,1}= \hat{\dot{x}}_{1,1} =39.42m/s x˙^2,1=x˙^1,1=39.42m/s
- 第2次迭代
一个采样周期过后,状态预测变为先验估计:
x ^ 2 , 1 = 30391.3 m \hat{x}_{2,1}=30391.3m x^2,1=30391.3m x ˙ ^ 2 , 1 = 39.42 m / s \hat{\dot{x}}_{2,1}= 39.42m/s x˙^2,1=39.42m/s
第1步
雷达进行一次测距:
z 2 = 30353 m z_{2}= 30353m z2=30353m
第2步
用状态更新方程计算当前的状态估计:
x ^ 2 , 2 = x ^ 2 , 1 + α ( z 2 − x ^ 2 , 1 ) = 30391.3 + 0.2 ( 30353 − 30391.3 ) = 30383.64 m \hat{x}_{2,2} = \hat{x}_{2,1}+ \alpha \left( z_{2}- \hat{x}_{2,1} \right) =30391.3+0.2 \left( 30353-30391.3 \right) = 30383.64m x^2,2=x^2,1+α(z2−x^2,1)=30391.3+0.2(30353−30391.3)=30383.64m x ˙ ^ 2 , 2 = x ˙ ^ 2 , 1 + β ( z 2 − x ^ 2 , 1 Δ t ) = 39.42 + 0.1 ( 30353 − 30391.3 5 ) = 38.65 m / s \hat{\dot{x}}_{2,2}= \hat{\dot{x}}_{2,1}+ \beta \left( \frac{z_{2}-\hat{x}_{2,1}}{ \Delta t} \right) = 39.42 + 0.1 \left( \frac{30353-30391.3}{5} \right) = 38.65m/s x˙^2,2=x˙^2,1+β(Δtz2−x^2,1)=39.42+0.1(530353−30391.3)=38.65m/s
第3步
用状态外插方程预测下一周期的状态:
x ^ 3 , 2 = x ^ 2 , 2 + Δ t x ˙ ^ 2 , 2 = 30383.64 + 5 × 38.65 = 30576.9 m \hat{x}_{3,2}= \hat{x}_{2,2}+ \Delta t\hat{\dot{x}}_{2,2} =30383.64+5 \times 38.65=30576.9m x^3,2=x^2,2+Δtx˙^2,2=30383.64+5×38.65=30576.9m x ˙ ^ 3 , 2 = x ˙ ^ 2 , 2 = 38.65 m / s \hat{\dot{x}}_{3,2}= \hat{\dot{x}}_{2,2} =38.65m/s x˙^3,2=x˙^2,2=38.65m/s
- 第3次迭代
z 3 = 30756 m z_{3}= 30756m z3=30756m x ^ 3 , 3 = 30576.9 + 0.2 ( 30756 − 30576.9 ) = 30612.73 m \hat{x}_{3,3}= 30576.9+0.2 \left( 30756 -30576.9 \right) = 30612.73m x^3,3=30576.9+0.2(30756−30576.9)=30612.73m x ˙ ^ 3 , 3 = 38.65 + 0.1 ( 30756 − 30576.9 5 ) = 42.2 m / s \hat{\dot{x}}_{3,3}= 38.65+0.1 \left( \frac{30756 - 30576.9}{5} \right) = 42.2m/s x˙^3,3=38.65+0.1(530756−30576.9)=42.2m/s x ^ 4 , 3 = 30612.73 + 5 × 42.2 = 30823.9 m \hat{x}_{4,3}= 30612.73+5 \times 42.2=30823.9m x^4,3=30612.73+5×42.2=30823.9m x ˙ ^ 4 , 3 = 42.2 m / s \hat{\dot{x}}_{4,3}= 42.2m/s x˙^4,3=42.2m/s
- 第4次迭代
z 4 = 30799 m z_{4}= 30799m z4=30799m x ^ 4 , 4 = 30823.9 + 0.2 ( 30799 − 30823.9 ) = 30818.93 m \hat{x}_{4,4}= 30823.9+0.2 \left( 30799-30823.9 \right) = 30818.93m x^4,4=30823.9+0.2(30799−30823.9)=30818.93m x ˙ ^ 4 , 4 = 42.2 + 0.1 ( 30799 − 30823.9 5 ) = 41.7 m / s \hat{\dot{x}}_{4,4}= 42.2+0.1 \left( \frac{30799-30823.9}{5} \right) = 41.7m/s x˙^4,4=42.2+0.1(530799−30823.9)=41.7m/s x ^ 5 , 4 = 30818.93 + 5 × 41.7 = 31027.6 m \hat{x}_{5,4}= 30818.93+5 \times 41.7=31027.6m x^5,4=30818.93+5×41.7=31027.6m x ˙ ^ 5 , 4 = 41.7 m / s \hat{\dot{x}}_{5,4}= 41.7m/s x˙^5,4=41.7m/s
- 第5次迭代
z 5 = 31018 m z_{5}= 31018m z5=31018m x ^ 5 , 5 = 31027.6 + 0.2 ( 31018 − 31027.6 ) = 31025.7 m \hat{x}_{5,5}= 31027.6+0.2 \left( 31018 -31027.6 \right) = 31025.7m x^5,5=31027.6+0.2(31018−31027.6)=31025.7m x ˙ ^ 5 , 5 = 41.7 + 0.1 ( 31018 − 31027.6 5 ) = 41.55 m / s \hat{\dot{x}}_{5,5}= 41.7+0.1 \left( \frac{31018 -31027.6}{5} \right) = 41.55m/s x˙^5,5=41.7+0.1(531018−31027.6)=41.55m/s x ^ 6 , 5 = 31025.7 + 5 × 41.55 = 31233.4 m \hat{x}_{6,5}= 31025.7+5 \times 41.55 = 31233.4m x^6,5=31025.7+5×41.55=31233.4m x ˙ ^ 6 , 5 = 41.55 m / s \hat{\dot{x}}_{6,5}= 41.55m/s x˙^6,5=41.55m/s
- 第6次迭代
z 6 = 31278 m z_{6}= 31278m z6=31278m x ^ 6 , 6 = 31233.4 + 0.2 ( 31278 − 31233.4 ) = 31242.3 m \hat{x}_{6,6}= 31233.4+0.2 \left( 31278 -31233.4 \right) = 31242.3m x^6,6=31233.4+0.2(31278−31233.4)=31242.3m x ˙ ^ 6 , 6 = 41.55 + 0.1 ( 31278 − 31233.4 5 ) = 42.44 m / s \hat{\dot{x}}_{6,6}= 41.55+0.1 \left( \frac{31278 -31233.4}{5} \right) = 42.44m/s x˙^6,6=41.55+0.1(531278−31233.4)=42.44m/s x ^ 7 , 6 = 31242.3 + 5 × 42.44 = 31454.5 m \hat{x}_{7,6}= 31242.3+5 \times 42.44 = 31454.5m x^7,6=31242.3+5×42.44=31454.5m x ˙ ^ 7 , 6 = 42.44 m / s \hat{\dot{x}}_{7,6}= 42.44m/s x˙^7,6=42.44m/s
- 第7次迭代
z 7 = 31276 m z_{7}= 31276m z7=31276m x ^ 7 , 7 = 31454.5 + 0.2 ( 31276 − 31454.5 ) = 31418.8 m \hat{x}_{7,7}= 31454.5+0.2 \left( 31276 -31454.5 \right) = 31418.8m x^7,7=31454.5+0.2(31276−31454.5)=31418.8m x ˙ ^ 7 , 7 = 42.44 + 0.1 ( 31276 − 31454.5 5 ) = 38.9 m / s \hat{\dot{x}}_{7,7}= 42.44+0.1 \left( \frac{31276 -31454.5}{5} \right) = 38.9m/s x˙^7,7=42.44+0.1(531276−31454.5)=38.9m/s x ^ 8 , 7 = 31418.8 + 5 × 38.9 = 31613.15 m \hat{x}_{8,7}= 31418.8+5 \times 38.9 = 31613.15m x^8,7=31418.8+5×38.9=31613.15m x ˙ ^ 8 , 7 = 38.9 m / s \hat{\dot{x}}_{8,7}= 38.9m/s x˙^8,7=38.9m/s
- 第8次迭代
z 8 = 31379 m z_{8}= 31379m z8=31379m x ^ 8 , 8 = 31613.15 + 0.2 ( 31379 − 31613.15 ) = 31566.3 m \hat{x}_{8,8}= 31613.15+0.2 \left( 31379 -31613.15 \right) = 31566.3m x^8,8=31613.15+0.2(31379−31613.15)=31566.3m x ˙ ^ 8 , 8 = 38.9 + 0.1 ( 31379 − 31613.15 5 ) = 34.2 m / s \hat{\dot{x}}_{8,8}= 38.9+0.1 \left( \frac{31379 -31613.15}{5} \right) = 34.2m/s x˙^8,8=38.9+0.1(531379−31613.15)=34.2m/s x ^ 9 , 8 = 31566.3 + 5 × 34.2 = 31737.24 m \hat{x}_{9,8}= 31566.3 + 5 \times 34.2 = 31737.24m x^9,8=31566.3+5×34.2=31737.24m x ˙ ^ 9 , 8 = 34.2 m / s \hat{\dot{x}}_{9,8}= 34.2m/s x˙^9,8=34.2m/s
- 第9次迭代
z 9 = 31748 m z_{9}= 31748m z9=31748m x ^ 9 , 9 = 31737.24 + 0.2 ( 31748 − 31737.24 ) = 31739.4 m \hat{x}_{9,9}= 31737.24+0.2 \left( 31748 -31737.24 \right) = 31739.4m x^9,9=31737.24+0.2(31748−31737.24)=31739.4m x ˙ ^ 9 , 9 = 34.2 + 0.1 ( 31748 − 31737.24 5 ) = 34.4 m / s \hat{\dot{x}}_{9,9}= 34.2+0.1 \left( \frac{31748 -31737.24}{5} \right) = 34.4m/s x˙^9,9=34.2+0.1(531748−31737.24)=34.4m/s x ^ 10 , 9 = 31739.4 + 5 × 34.4 = 31911.4 m \hat{x}_{10,9}= 31739.4+5 \times 34.4=31911.4m x^10,9=31739.4+5×34.4=31911.4m x ˙ ^ 10 , 9 = 34.4 m / s \hat{\dot{x}}_{10,9}=34.4m/s x˙^10,9=34.4m/s
- 第10次迭代
z 10 = 32175 m z_{10}= 32175m z10=32175m x ^ 10 , 10 = 31911.4 + 0.2 ( 32175 − 31911.4 ) = 31964.1 m \hat{x}_{10,10}= 31911.4+0.2 \left( 32175 -31911.4 \right) = 31964.1m x^10,10=31911.4+0.2(32175−31911.4)=31964.1m x ˙ ^ 10 , 10 = 34.4 + 0.1 ( 32175 − 31911.4 5 ) = 39.67 m / s \hat{\dot{x}}_{10,10}= 34.4+0.1 \left( \frac{32175 -31911.4}{5} \right) = 39.67m/s x˙^10,10=34.4+0.1(532175−31911.4)=39.67m/s x ^ 11 , 10 = 31964.1 + 5 × 39.67 = 32162.45 m \hat{x}_{11,10}= 31964.1+5 \times 39.67 = 32162.45m x^11,10=31964.1+5×39.67=32162.45m x ˙ ^ 11 , 10 = 39.67 m / s \hat{\dot{x}}_{11,10}= 39.67m/s x˙^11,10=39.67m/s
下表汇总了测量值和估计值。
| 变量 | 数值 |
|---|---|
| n n n | 1 2 3 4 5 6 7 8 9 10 |
| z n z_{n} zn | 30171 30353 30756 30799 31018 31278 31276 31379 31748 32175 |
| x ^ n , n \hat{x}_{n,n} x^n,n | 30194.2 30383.64 30612.73 30818.93 31025.7 31242.3 31418.8 31566.3 31739.4 31964.1 |
| x ^ ˙ n , n \dot{\hat{x}}_{n,n} x^˙n,n | 39.42 38.65 42.2 41.7 41.55 42.44 38.9 34.2 34.4 39.67 |
| x ^ n + 1 , n \hat{x}_{n+1,n} x^n+1,n | 30391.3 30576.9 30823.9 31027.6 31233.4 31454.5 31613.15 31737.24 31911.4 32162.45 |
| x ^ ˙ n + 1 , n \dot{\hat{x}}_{n+1,n} x^˙n+1,n | 39.42 38.65 42.2 41.7 41.55 42.44 38.9 34.2 34.4 39.67 |
结果分析
下图中列出了测量值、估计值以及真值。
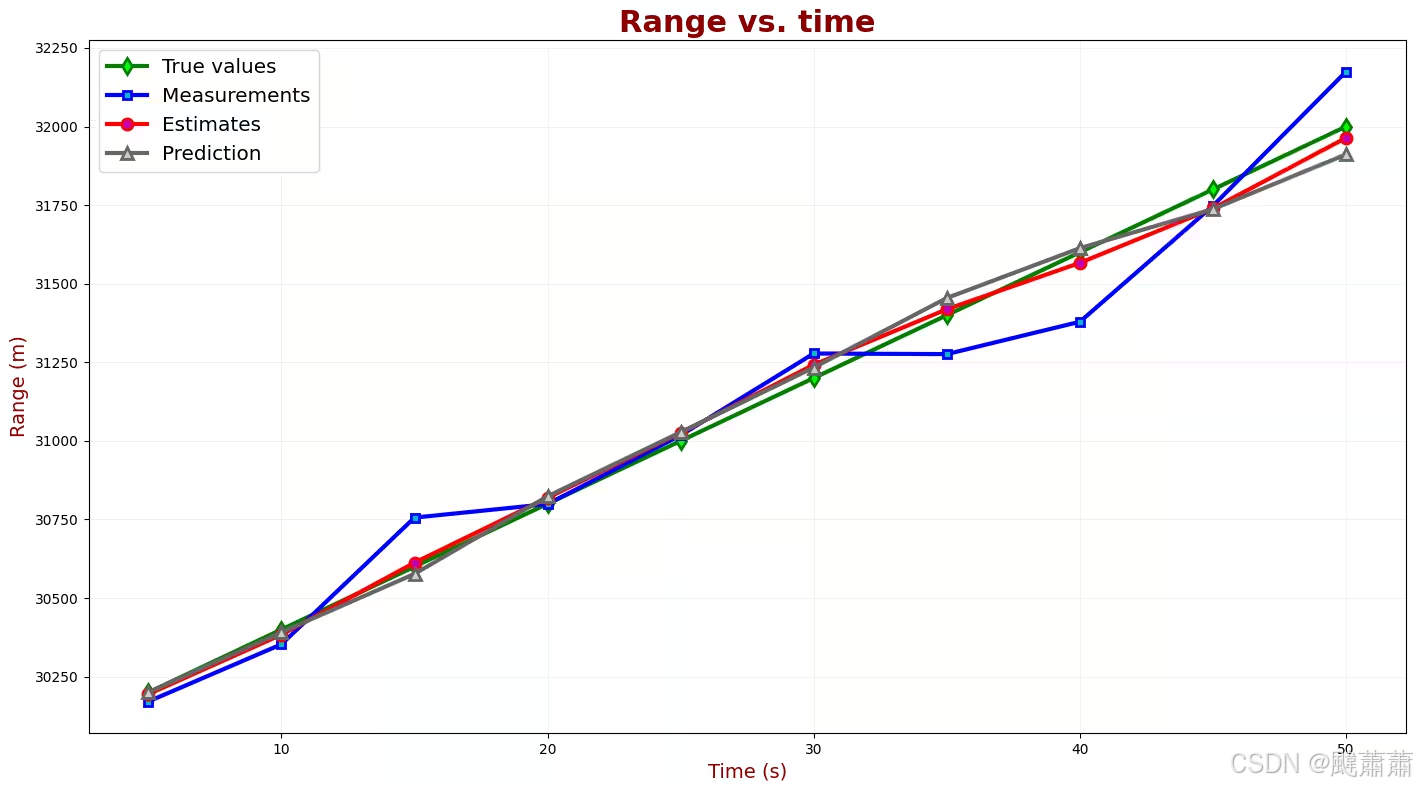
我们的估计算法对测量值有平滑效果,并且能收敛到真值。
用较大的
α
\alpha
α 和
β
\beta
β
下图描述了
α
=
0.8
\alpha = 0.8
α=0.8、
β
=
0.5
\beta = 0.5
β=0.5 时的真值、测量值和估计值。
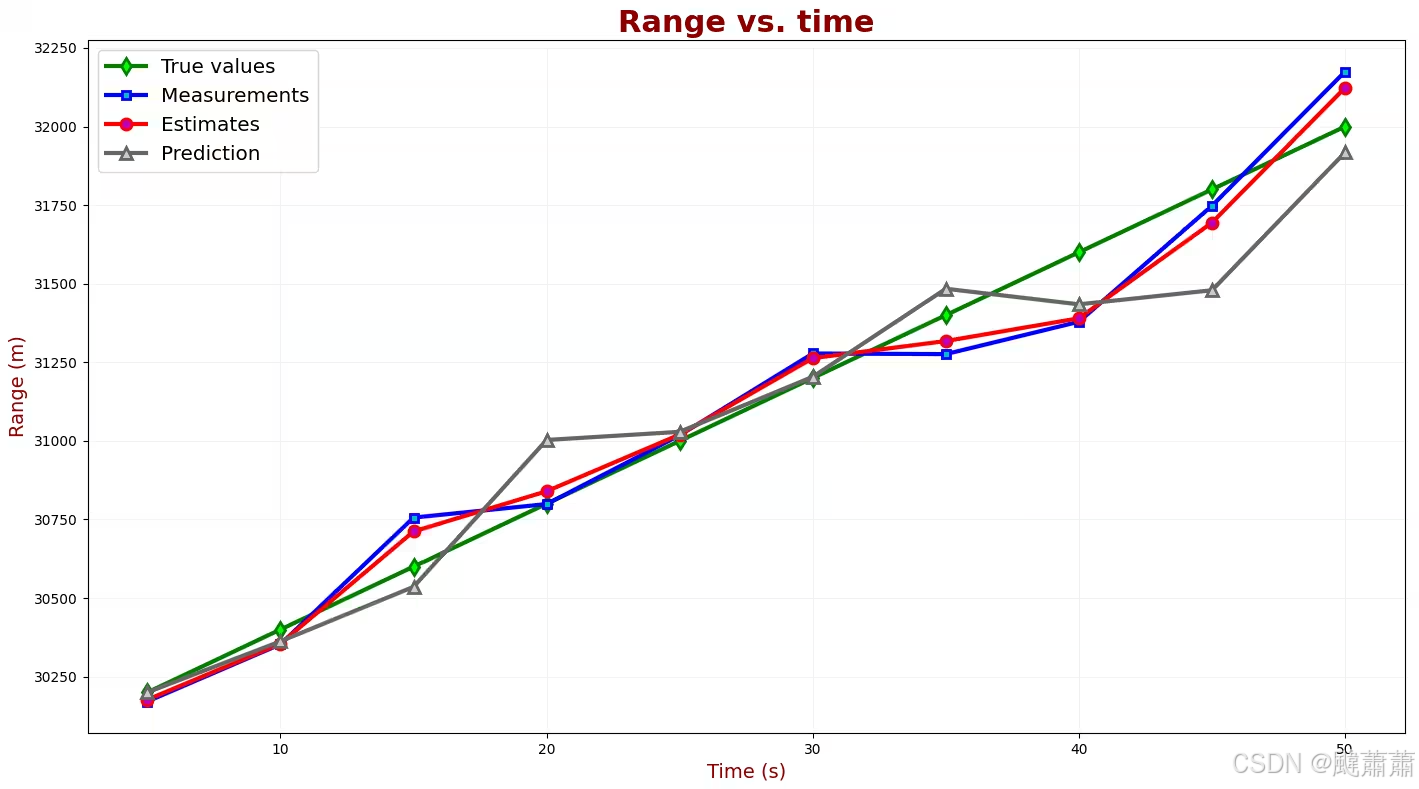
滤波器的平滑效果降低了很多。当前估计值非常接近测量值,预测的误差也相对较高。
那么我们应该一直选取较低的 α \alpha α 和 β \beta β 吗?
答案是否定的。 α \alpha α 和 β \beta β 的值应该依测量精度而定。如果测量设备精度很高,例如激光雷达,较高的 α \alpha α 和 β \beta β 会比较好,会更信赖测量值,对于本例则滤波器对飞行器速度的变化响应更快;如果测量设备精度很低,应该用较低的 α \alpha α 和 β \beta β,会更信赖预测值,对于本例则滤波器对测量不确定性(误差)的平滑效果会更好,但滤波器对飞行器速度的变化响应就会慢得多。
示例小结
我们推导了 α − β \alpha - \beta α−β 滤波器的状态更新方程,并且还学到了状态外插方程。我们用 α − β \alpha - \beta α−β 滤波器设计了一个一维动态系统估计算法,并用它数值求解了一个匀速运动目标的状态估计问题。





















 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








