
本文地址:https://goodgoodstudy.blog.youkuaiyun.com/article/details/112008150
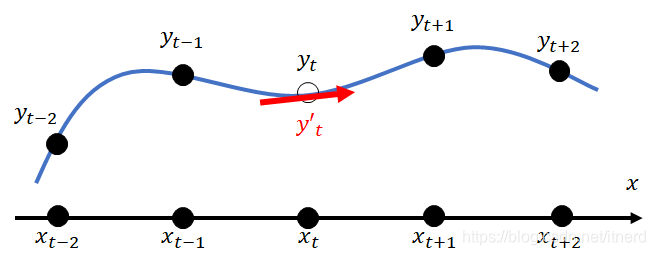
原理:利用指定点 yty_tyt 周围的四个点(yt−2,yt−1,yt+2,yt+2)(y_{t-2}, y_{t-1}, y_{t+2},y_{t+2})(yt−2,yt−1,yt+2,yt+2)构造 拉格朗日插值曲线:
y(x)=yt−2(x−xt−1)(x−xt+1)(x−xt+2)(xt−2−xt−1)(xt−2−xt+1)(xt−2−xt+2)+yt−1(x−xt−2)(x−xt+1)(x−xt+2)(xt−1−xt−2)(xt−1−xt+1)(xt−1−xt+2)+yt+1(x−xt−2)(x−xt−1)(x−xt+2)(xt+1−xt−2)(xt+1−xt−1)(xt+1−xt+2)+yt+2(x−xt−2)(x−xt−1)(x−xt+1)(xt+2−xt−2)(xt+2−xt−1)(xt+2−xt+1)
\begin{aligned}
y(x) =& y_{t-2}\frac{(x-x_{t-1})(x-x_{t+1})(x-x_{t+2})}{(x_{t-2}-x_{t-1})(x_{t-2}-x_{t+1})(x_{t-2}-x_{t+2})} \\
\\
&+y_{t-1}\frac{(x-x_{t-2})(x-x_{t+1})(x-x_{t+2})}{(x_{t-1}-x_{t-2})(x_{t-1}-x_{t+1})(x_{t-1}-x_{t+2})} \\
\\
&+y_{t+1}\frac{(x-x_{t-2})(x-x_{t-1})(x-x_{t+2})}{(x_{t+1}-x_{t-2})(x_{t+1}-x_{t-1})(x_{t+1}-x_{t+2})} \\
\\
&+y_{t+2}\frac{(x-x_{t-2})(x-x_{t-1})(x-x_{t+1})}{(x_{t+2}-x_{t-2})(x_{t+2}-x_{t-1})(x_{t+2}-x_{t+1})}
\end{aligned}
y(x)=yt−2(xt−2−xt−1)(xt−2−xt+1)(xt−2−xt+2)(x−xt−1)(x−xt+1)(x−xt+2)+yt−1(xt−1−xt−2)(xt−1−xt+1)(xt−1−xt+2)(x−xt−2)(x−xt+1)(x−xt+2)+yt+1(xt+1−xt−2)(xt+1−xt−1)(xt+1−xt+2)(x−xt−2)(x−xt−1)(x−xt+2)+yt+2(xt+2−xt−2)(xt+2−xt−1)(xt+2−xt+1)(x−xt−2)(x−xt−1)(x−xt+1)
分母是可以直接写出来的,记 h≡xt−xt−1h \equiv x_t - x_{t-1}h≡xt−xt−1 为自变量间隔:
y(x)=yt−2(x−xt−1)(x−xt+1)(x−xt+2)(−h)(−3h)(−4h)+yt−1(x−xt−2)(x−xt+1)(x−xt+2)(h)(−2h)(−3h)+yt+1(x−xt−2)(x−xt−1)(x−xt+2)(3h)(2h)(−h)+yt+2(x−xt−2)(x−xt−1)(x−xt+1)(4h)(3h)(h)=[−yt−2(x−xt−1)(x−xt+1)(x−xt+2)+2yt−1(x−xt−2)(x−xt+1)(x−xt+2)−2yt+1(x−xt−2)(x−xt−1)(x−xt+2)+yt+2(x−xt−2)(x−xt−1)(x−xt+1)]112h3
\begin{aligned}
y(x) =& y_{t-2}\frac{(x-x_{t-1})(x-x_{t+1})(x-x_{t+2})}{(-h)(-3h)(-4h)} \\\\
&+y_{t-1}\frac{(x-x_{t-2})(x-x_{t+1})(x-x_{t+2})}{(h)(-2h)(-3h)} \\
\\
&+y_{t+1}\frac{(x-x_{t-2})(x-x_{t-1})(x-x_{t+2})}{(3h)(2h)(-h)} \\
\\
&+y_{t+2}\frac{(x-x_{t-2})(x-x_{t-1})(x-x_{t+1})}{(4h)(3h)(h)} \\\\
=&[ -y_{t-2}(x-x_{t-1})(x-x_{t+1})(x-x_{t+2})\\
& + 2y_{t-1}(x-x_{t-2})(x-x_{t+1})(x-x_{t+2})\\
& -2y_{t+1}(x-x_{t-2})(x-x_{t-1})(x-x_{t+2})\\
& + y_{t+2}(x-x_{t-2})(x-x_{t-1})(x-x_{t+1}) ]\frac{1}{12h^3}
\end{aligned}
y(x)==yt−2(−h)(−3h)(−4h)(x−xt−1)(x−xt+1)(x−xt+2)+yt−1(h)(−2h)(−3h)(x−xt−2)(x−xt+1)(x−xt+2)+yt+1(3h)(2h)(−h)(x−xt−2)(x−xt−1)(x−xt+2)+yt+2(4h)(3h)(h)(x−xt−2)(x−xt−1)(x−xt+1)[−yt−2(x−xt−1)(x−xt+1)(x−xt+2)+2yt−1(x−xt−2)(x−xt+1)(x−xt+2)−2yt+1(x−xt−2)(x−xt−1)(x−xt+2)+yt+2(x−xt−2)(x−xt−1)(x−xt+1)]12h31
接下来就是求该三次函数在 xtx_txt 处的导数 y′(xt)y'(x_{t})y′(xt)
y′(x)={−yt−2[(x−xt+1)(x−xt+2)+(x−xt−1)(x−xt+2)+(x−xt−1)(x−xt+1)]+2yt−1[(x−xt+1)(x−xt+2)+(x−xt−2)(x−xt+2)+(x−xt−2)(x−xt+1)]−2yt+1[(x−xt−1)(x−xt+2)+(x−xt−2)(x−xt+2)+(x−xt−2)(x−xt−1)]+yt+2[(x−xt−1)(x−xt+1)+(x−xt−2)(x−xt+1)+(x−xt−2)(x−xt−1)]}112h3
\begin{aligned}
y'(x) =& \{ -y_{t-2}[(x-x_{t+1})(x-x_{t+2})+(x-x_{t-1})(x-x_{t+2})+(x-x_{t-1})(x-x_{t+1})]\\
\\
& + 2y_{t-1}[(x-x_{t+1})(x-x_{t+2})+(x-x_{t-2})(x-x_{t+2})+(x-x_{t-2})(x-x_{t+1})]\\
\\
& -2y_{t+1}[(x-x_{t-1})(x-x_{t+2})+(x-x_{t-2})(x-x_{t+2})+(x-x_{t-2})(x-x_{t-1})]\\
\\
& + y_{t+2}[(x-x_{t-1})(x-x_{t+1})+(x-x_{t-2})(x-x_{t+1})+(x-x_{t-2})(x-x_{t-1})] \}\frac{1}{12h^3}
\end{aligned}
y′(x)={−yt−2[(x−xt+1)(x−xt+2)+(x−xt−1)(x−xt+2)+(x−xt−1)(x−xt+1)]+2yt−1[(x−xt+1)(x−xt+2)+(x−xt−2)(x−xt+2)+(x−xt−2)(x−xt+1)]−2yt+1[(x−xt−1)(x−xt+2)+(x−xt−2)(x−xt+2)+(x−xt−2)(x−xt−1)]+yt+2[(x−xt−1)(x−xt+1)+(x−xt−2)(x−xt+1)+(x−xt−2)(x−xt−1)]}12h31
所以
y′(xt)={−yt−2[(xt−xt+1)(xt−xt+2)+(xt−xt−1)(xt−xt+2)+(xt−xt−1)(xt−xt+1)]+2yt−1[(xt−xt+1)(xt−xt+2)+(xt−xt−2)(xt−xt+2)+(xt−xt−2)(xt−xt+1)]−2yt+1[(xt−xt−1)(xt−xt+2)+(xt−xt−2)(xt−xt+2)+(xt−xt−2)(xt−xt−1)]+yt+2[(xt−xt−1)(xt−xt+1)+(xt−xt−2)(xt−xt+1)+(xt−xt−2)(xt−xt−1)]}112h3={−yt−2[(−h)(−2h)+(h)(−2h)+(h)(−h)]+2yt−1[(−h)(−2h)+(2h)(−2h)+(2h)(−h)]−2yt+1[(h)(−2h)+(2h)(−2h)+(2h)(h)]+yt+2[(h)(−h)+(2h)(−h)+(2h)(h)]}112h3=(yt−2−8yt−1+8yt+1−yt+2)112h
\begin{aligned}
y'(x_t) =& \{ -y_{t-2}[(x_t-x_{t+1})(x_t-x_{t+2})+(x_t-x_{t-1})(x_t-x_{t+2})+(x_t-x_{t-1})(x_t-x_{t+1})]\\
\\
& + 2y_{t-1}[(x_t-x_{t+1})(x_t-x_{t+2})+(x_t-x_{t-2})(x_t-x_{t+2})+(x_t-x_{t-2})(x_t-x_{t+1})]\\
\\
& -2y_{t+1}[(x_t-x_{t-1})(x_t-x_{t+2})+(x_t-x_{t-2})(x_t-x_{t+2})+(x_t-x_{t-2})(x_t-x_{t-1})]\\
\\
& + y_{t+2}[(x_t-x_{t-1})(x_t-x_{t+1})+(x_t-x_{t-2})(x_t-x_{t+1})+(x_t-x_{t-2})(x_t-x_{t-1})] \}\frac{1}{12h^3} \\
\\
=& \{ -y_{t-2}[(-h)(-2h)+(h)(-2h)+(h)(-h)]\\
\\
& + 2y_{t-1}[(-h)(-2h)+(2h)(-2h)+(2h)(-h)]\\
\\
& -2y_{t+1}[(h)(-2h)+(2h)(-2h)+(2h)(h)]\\
\\
& + y_{t+2}[(h)(-h)+(2h)(-h)+(2h)(h)] \}\frac{1}{12h^3} \\
\\
=& ( y_{t-2} -8y_{t-1} +8y_{t+1}- y_{t+2} )\frac{1}{12h} \\
\end{aligned}
y′(xt)==={−yt−2[(xt−xt+1)(xt−xt+2)+(xt−xt−1)(xt−xt+2)+(xt−xt−1)(xt−xt+1)]+2yt−1[(xt−xt+1)(xt−xt+2)+(xt−xt−2)(xt−xt+2)+(xt−xt−2)(xt−xt+1)]−2yt+1[(xt−xt−1)(xt−xt+2)+(xt−xt−2)(xt−xt+2)+(xt−xt−2)(xt−xt−1)]+yt+2[(xt−xt−1)(xt−xt+1)+(xt−xt−2)(xt−xt+1)+(xt−xt−2)(xt−xt−1)]}12h31{−yt−2[(−h)(−2h)+(h)(−2h)+(h)(−h)]+2yt−1[(−h)(−2h)+(2h)(−2h)+(2h)(−h)]−2yt+1[(h)(−2h)+(2h)(−2h)+(2h)(h)]+yt+2[(h)(−h)+(2h)(−h)+(2h)(h)]}12h31(yt−2−8yt−1+8yt+1−yt+2)12h1
这就是计算一阶导数的四阶中心差分格式!







 该文详细介绍了如何利用四阶中心差分公式来计算一阶导数,这种方法基于拉格朗日插值原理,通过周围四个点的数据构造插值曲线,并在目标点求导。最终公式展示了如何从四个相邻点的数据推导出在某点的导数值。
该文详细介绍了如何利用四阶中心差分公式来计算一阶导数,这种方法基于拉格朗日插值原理,通过周围四个点的数据构造插值曲线,并在目标点求导。最终公式展示了如何从四个相邻点的数据推导出在某点的导数值。


















 7万+
7万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










