路径规划--多边形障碍区域的处理

Combinatorial methods（组合逻辑方法）必须构造一个有限的数据结构来精确地编码规划问题。单元分解算法实现了将$C_{free}$划分为一组称为cell单元的有限区域。单元分解应满足三个特性：

• 计算单元内从点到点的路径必须非常容易。例如，如果每个单元都是凸的，那么单元中的任何一对点都可以通过线段连接。
• 可以很容易地提取单元的邻接信息来构建路线图。
• 对于给定的$q_I$和$q_G$，必须有效地确定其包含于单元内。
  如果单元分解满足这些性质，那么运动规划问题就简化为一个图搜索问题。当提前知道整个图（如卫星地图、SLAM离线地图），即可搜寻可行规划。

垂直单元分解

vertical cell decomposition（垂直单元分解法）将$C_{free}$划分为一个2维单元和1个一维单元的有限集合。每个2维单元要么是有垂直边的梯形，要么是三角形（退化的梯形）
因此，这种方法有时被称为梯形分解。分解定义如下。让$P$表示用于定义$C_{obs}$的顶点集。对于每个$p\in P$，尝试通过$C_{free}$向上和向下扩展光线，直到达到$C_{obs}$。如图所示，分解有四种可能的情况，这取决于是否可以在上下两个方向中的每一个方向上延伸。
1）向上和向下延伸，2）仅向上，3）仅向下，4）不可能延伸

对于垂直分解，如果不考虑所有数据点在某个随机方向上都受到微量扰动，这些问题并不太难处理；但是，一般来说，必须意识到这一困难在大多数情况下是不容易解决的。

下图显示了算法是如何进行的。最初，$L$为空且使用双连接的边列表来表示$C_{free}$。对于每个事件，都会发生上图中的四种情况之一。通过使用平衡二叉树更新$L$，可以在$O(\lg n)$内确定$p$上下的边。这比检查每个段产生的$O(n)$要好得多。根据四种情况，对$L$进行不同的更新。如果出现第一种情况，则插入两条不同的边。
一种更优雅的方法是在每个事件中递增地构建$G$。事实上，只要正确构建$G$，并为每个单元获取采样点，就可以不去维护双连接边列表所需的所有指针。我们甚至可以更进一步，忘记单元分解，直接在相邻单元的所有采样点之间建立线段路径的拓扑图。

查询单元的路径规划可以通过简单的“连接点”形成。$q_0$，$q_1$，$q_2$，$\dots$，$q_{k-1}$，$q_k$表示图$G$中路径上的采样点。每个单元格都有一个被穿过的采样点。规划路径$\tau :[0,1]\to C_{free}$是通过设置$\tau (0)=q_I$，$\tau (1)=q_G$，并通过沿着最短路径访问序列中从$q_0$到$q_k$ 的每个点而形成的。

在选择采样点时，重要的是确保从一个单元的采样点到其相邻单元的采样点的每个路径段都是无冲突的。

窄通道

最大间隙路线尽量保持远离$C_{obs}$，如图中的走廊所示。由于移动机器人的精确位置很难测量和控制，因此在移动机器人应用中，更倾向于采用求解出的规划路径。沿着最大间隙路线（或称广义Voronoi图收缩方法）可以减少由于这些不确定性引起的碰撞机会。它是Voronoi图从点到多边形的情况的推广。路径图边缘上的每个点与$C_{obs}$边界上的两个点等距。每个路线图顶点对应于两个或多个路线图边的交点，因此与$C_{obs}$边界上的三个或多个点等距。
The retraction term（撤回项）来自拓扑学，并提供了一个关于该方法的良好直觉。子空间$S$是拓扑空间$X$的变形收缩，如果连续同伦（即：两个对象间的“连续变化”，两个拓扑空间如果可以通过一系列连续的形变从一个变到另一个），$h:X\times [0,1]\to X$可以定义如下：

• $h(x,0)=x$, $x\in X$。
• $h(x,1)$是一个连续函数，它将$X$的每个元素映射到$S$的某个元素。
• 当$t\in [0,1]$，任意$s\in S$都有$h(s,t)=s$。

直觉是$C_{free}$通过同伦逐渐变薄，直到$S$被包含的过程。这种收缩过程可以近似想象为（不断地）在$C_{free}$的全部边界周围削掉薄薄的一层。如果反复迭代，最大间隙路径是唯一剩下的部分。
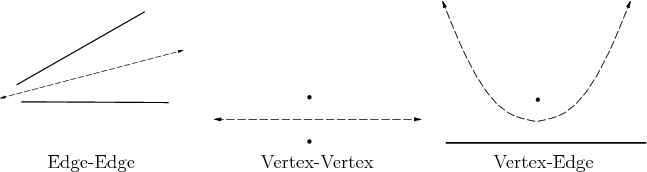
为了构建最大间隙路线图，再次使用特征概念。让特征集引用$C_{obs}$的所有边和顶点集。规划路径的候选路径由每对特性生成。这导致了一个简单的$O(n^4)$算法，如下所示。边～边、点～点为直线，点～边为抛物线。实际上，位于最大间隙路线图上的路径的部分是通过交叉曲线来确定的。有几种算法提供更好的时间复杂度，但它们更难以实现。最著名的算法为$O(n\lg n)$，其中$n$是曲线的数目。