意义
傅里叶变换具有唯一性,傅氏变换的性质揭示了信号的时域特性和频域特性之间的确定的内在联系,讨论傅里叶变换的性质,目的在于:了解特性的内在联系;用性质求 F ( ω ) F(\omega) F(ω);了解在通信系统领域中的应用
1. 对称性质
- 性质
若 f ( t ) ↔ F ( ω ) f(t)\leftrightarrow F(\omega) f(t)↔F(ω),则 F ( t ) ↔ 2 π f ( − ω ) F(t)\leftrightarrow 2\pi f(-\omega) F(t)↔2πf(−ω)
若f(t)为偶函数,则 F ( t ) ↔ 2 π f ( ω ) F(t)\leftrightarrow 2\pi f(\omega) F(t)↔2πf(ω) - 意义
若F(t)形状与 F ( ω ) F(\omega) F(ω)相同, ( ω → t ) (\omega \to t) (ω→t)
则F(t)的频谱函数形状与f(t)形状相同, ( t → ω ) (t\to\omega) (t→ω),幅度差2 π \pi π
2. 线性性质
- 性质
若 f 1 ( t ) ↔ F 1 ( ω ) , f 2 ( t ) ↔ F 2 ( ω ) f_1(t)\leftrightarrow F_1(\omega), f_2(t)\leftrightarrow F_2(\omega) f1(t)↔F1(ω),f2(t)↔F2(ω)
则 c 1 f 1 ( t ) + c 2 f 2 ( t ) ↔ c 1 F 1 ( ω ) + c 2 F 2 ( ω ) c_1f_1(t) + c_2f_2(t)\leftrightarrow c_1F_1(\omega)+c_2F_2(\omega) c1f1(t)+c2f2(t)↔c1F1(ω)+c2F2(ω)
3. 奇偶虚实性
若
f
(
t
)
↔
F
(
ω
)
f(t)\leftrightarrow F(\omega)
f(t)↔F(ω),则
f
(
−
t
)
↔
F
(
−
ω
)
f(-t)\leftrightarrow F(-\omega)
f(−t)↔F(−ω)
证明:由定义
F
[
f
(
t
)
]
=
∫
−
∞
∞
f
(
t
)
e
−
j
ω
t
d
e
=
F
(
ω
)
F[f(t)] = \int_{-\infty}^{\infty}f(t)e^{-j\omega t}de = F(\omega)
F[f(t)]=∫−∞∞f(t)e−jωtde=F(ω)可以得到
F
[
f
(
t
)
]
=
∫
−
∞
∞
f
(
−
t
)
e
−
j
ω
t
d
t
=
∫
−
∞
∞
f
(
u
)
e
−
j
(
−
ω
)
u
d
u
=
F
(
−
ω
)
F[f(t)]=\int_{-\infty}^{\infty}f(-t)e^{-j\omega t}dt = \int_{-\infty}^{\infty}f(u)e^{-j(-\omega)u}du = F(-\omega)
F[f(t)]=∫−∞∞f(−t)e−jωtdt=∫−∞∞f(u)e−j(−ω)udu=F(−ω)
若
f
(
t
)
↔
F
(
ω
)
f(t)\leftrightarrow F(\omega)
f(t)↔F(ω),则
f
(
−
t
)
↔
F
∗
(
ω
)
f(-t)\leftrightarrow F^*(\omega)
f(−t)↔F∗(ω)
证明:设f(t)是实函数
F
(
ω
)
=
∫
−
∞
∞
f
(
t
)
e
−
j
ω
t
d
t
=
∫
−
∞
∞
f
(
t
)
c
o
s
ω
t
d
t
−
j
∫
−
∞
∞
f
(
t
)
s
i
n
ω
t
d
t
F(\omega)=\int_{-\infty}^{\infty}f(t)e^{-j\omega t}dt = \int_{-\infty}^{\infty}f(t)cos\omega tdt - j\int_{-\infty}^{\infty}f(t)sin\omega tdt
F(ω)=∫−∞∞f(t)e−jωtdt=∫−∞∞f(t)cosωtdt−j∫−∞∞f(t)sinωtdt
{
R
(
ω
)
=
∫
−
∞
∞
f
(
t
)
c
o
s
ω
t
d
t
关于
ω
的偶函数
,
R
(
ω
)
=
R
(
−
ω
)
X
(
ω
)
=
∫
−
∞
∞
f
(
t
)
s
i
n
ω
t
d
t
关于
ω
的奇函数
,
X
(
ω
)
=
−
X
(
−
ω
)
\begin{cases} R(\omega) = \int_{-\infty}^{\infty}f(t)cos\omega tdt \quad 关于\omega 的偶函数, R(\omega)=R(-\omega)\\ X(\omega) = \int_{-\infty}^{\infty}f(t)sin\omega tdt \quad 关于\omega的奇函数, X(\omega) = -X(-\omega) \end{cases}
{R(ω)=∫−∞∞f(t)cosωtdt关于ω的偶函数,R(ω)=R(−ω)X(ω)=∫−∞∞f(t)sinωtdt关于ω的奇函数,X(ω)=−X(−ω)
∴
F
(
−
ω
)
=
F
∗
(
ω
)
\therefore F(-\omega) = F^*(\omega)
∴F(−ω)=F∗(ω)
4. 尺度变换性质
- 性质
若 F ( t ) ↔ F ( ω ) ,则 f ( a t ) ↔ 1 ∣ a ∣ F ( ω a ) F(t)\leftrightarrow F(\omega),则f(at)\leftrightarrow \frac{1}{|a|}F(\frac{\omega}{a}) F(t)↔F(ω),则f(at)↔∣a∣1F(aω), a为非零函数 - 证明
F [ f ( a t ) ] = ∫ − ∞ ∞ f ( a t ) e − j ω t d t F[f(at)]=\int_{-\infty}^{\infty}f(at)e^{-j\omega t}dt F[f(at)]=∫−∞∞f(at)e−jωtdt
当a>0,令 x = a t , d t = 1 a d x x=at,dt=\frac{1}{a}dx x=at,dt=a1dx
当a<0,令 x = − ∣ a ∣ t , d t = − 1 ∣ a ∣ d x x = -|a|t, dt = \frac{-1}{|a|}dx x=−∣a∣t,dt=∣a∣−1dx - 意义
(1)0<a<1 时域扩展,频带压缩(脉冲持续时间增加a倍,变化慢了,信号在频域的频带压缩a倍。高频分量减少,幅度上升a倍)
(2)a>1 时域压缩,频域扩展a倍(持续时间短,变化快,信号在频域高频分量增加,频带展宽,各分量的幅度下降a倍,说明:信号的持续时间与信号占有频带成反比,有时为加速信号的传递,要将信号持续时间压缩,则要以展开频带为代价)
(3)a = -1, f ( t ) → f ( − t ) , F ( ω ) → F ( − ω ) = F ∗ ( ω ) f(t) \to f(-t), F(\omega)\to F(-\omega)=F^*(\omega) f(t)→f(−t),F(ω)→F(−ω)=F∗(ω)
5. 时移特性
- 性质
若 f ( t ) ↔ F ( ω ) , 则 f ( t − t 0 ) ↔ F ( ω ) e − j ω t 0 f(t)\leftrightarrow F(\omega), 则f(t-t_0)\leftrightarrow F(\omega)e^{-j\omega t_0} f(t)↔F(ω),则f(t−t0)↔F(ω)e−jωt0
若 F ( ω ) = ∣ F ( ω ) ∣ e j ϕ ( ω ) , 则 f ( t − t 0 ) ↔ ∣ F ( ω ) ∣ ⋅ e j [ Φ ( ω ) − ω t 0 ] F(\omega)=|F(\omega)|e^{j\phi(\omega)}, 则f(t-t_0)\leftrightarrow |F(\omega)|\cdot e^{j[\Phi(\omega)-\omega t_0]} F(ω)=∣F(ω)∣ejϕ(ω),则f(t−t0)↔∣F(ω)∣⋅ej[Φ(ω)−ωt0]
幅度频谱无变化,只影响相位频谱
相移 ω t 0 { 右 − ω t 0 左 ω t 0 相移\omega t_0 \begin{cases} 右 \quad \quad -\omega t_0 \\ 左 \quad \quad \quad \omega t_0 \end{cases} 相移ωt0{右−ωt0左ωt0
6. 时移加尺度变换
(1)性质:若
f
(
t
)
↔
F
(
ω
)
,则
f
(
a
t
+
b
)
↔
1
∣
a
∣
F
(
ω
a
)
⋅
e
j
ω
b
a
,
a
≠
0
f(t)\leftrightarrow F(\omega),则f(at+b)\leftrightarrow \frac{1}{|a|}F(\frac{\omega}{a})\cdot e^{j\omega \frac{b}{a}}, a \neq 0
f(t)↔F(ω),则f(at+b)↔∣a∣1F(aω)⋅ejωab,a=0
(2)证明:(仿
δ
(
a
t
)
=
1
∣
a
∣
δ
(
t
)
\delta(at)=\frac{1}{|a|}\delta(t)
δ(at)=∣a∣1δ(t)的证明过程
7. 时域微分性质
(1)性质
若
f
(
t
)
↔
F
(
ω
)
,则
f
′
(
t
)
↔
j
ω
F
(
ω
)
f(t)\leftrightarrow F(\omega),则f^{'}(t)\leftrightarrow j\omega F(\omega)
f(t)↔F(ω),则f′(t)↔jωF(ω)
一般情况下,
f
(
n
)
(
t
)
↔
(
j
ω
)
n
F
(
ω
)
f^{(n)}(t)\leftrightarrow (j\omega)^nF(\omega)
f(n)(t)↔(jω)nF(ω)
若已知
F
∣
f
(
n
)
(
t
)
∣
,
则
F
(
ω
)
=
F
∣
f
(
n
)
(
t
)
∣
(
j
ω
)
n
F|f^{(n)}(t)|, 则F(\omega)=\frac{F|f^{(n)}(t)|}{(j\omega)^n}
F∣f(n)(t)∣,则F(ω)=(jω)nF∣f(n)(t)∣
(2)物理意义
F
[
f
′
(
t
)
]
=
j
w
F
(
ω
)
{
幅度乘
ω
相位增加,
j
→
90
∘
F[f^{'}(t)]=jwF(\omega) \begin{cases} 幅度乘\omega \\ 相位增加,j \to 90^{\circ} \end{cases}
F[f′(t)]=jwF(ω){幅度乘ω相位增加,j→90∘
如果f(t)中由确定的直流分量,应先取出单独求傅里叶变换,余下部分再用微分性质
8. 频域微分性质
性质
若
f
(
t
)
↔
F
(
ω
)
,
则
t
f
(
t
)
↔
j
d
F
(
ω
)
/
d
ω
f(t)\leftrightarrow F(\omega), 则tf(t)\leftrightarrow jdF(\omega)/d\omega
f(t)↔F(ω),则tf(t)↔jdF(ω)/dω
−
j
t
f
(
t
)
↔
d
F
(
ω
)
/
d
ω
-jtf(t)\leftrightarrow dF(\omega)/d\omega
−jtf(t)↔dF(ω)/dω
(
−
j
t
)
n
f
(
t
)
↔
d
n
F
(
ω
)
d
ω
n
(-jt)^nf(t)\leftrightarrow \frac{d^nF(\omega)}{d\omega^n}
(−jt)nf(t)↔dωndnF(ω)或
t
n
f
(
t
)
↔
(
j
)
n
F
n
(
ω
)
t^nf(t)\leftrightarrow (j)^nF^n(\omega)
tnf(t)↔(j)nFn(ω)
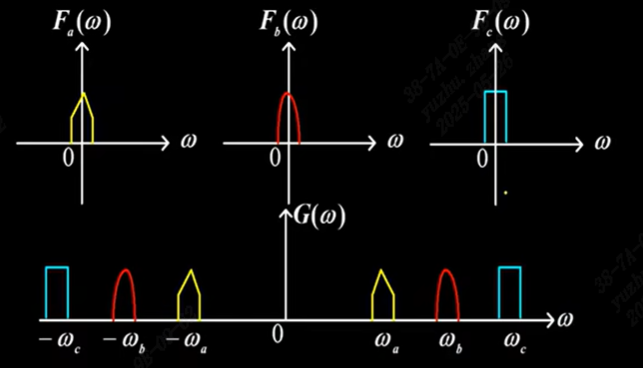
9. 频移性质
- 性质:若 f ( t ) ↔ F ( ω ) 则 { f ( t ) e j ω 0 t ↔ F ( ω − ω 0 ) f ( t ) e − j ω 0 t ↔ F ( ω + ω 0 ) ω 0 为常数,注意 ± 号 f(t)\leftrightarrow F(\omega) 则\begin{cases} f(t)e^{j\omega_0t}\leftrightarrow F(\omega-\omega_0) \\ f(t)e^{-j\omega_0t}\leftrightarrow F(\omega + \omega_0) \end{cases}\quad \omega_0为常数,注意\pm号 f(t)↔F(ω)则{f(t)ejω0t↔F(ω−ω0)f(t)e−jω0t↔F(ω+ω0)ω0为常数,注意±号
- 说明:时域f(t)乘
e
j
ω
0
t
e^{j\omega_0 t}
ejω0t, 频域频谱搬移——右移
ω
0
\omega_0
ω0
\quad \quad 时域f(t)乘 e − j ω 0 t e^{-j\omega_0 t} e−jω0t, 频域频谱搬移——左移 ω 0 \omega_0 ω0 - 应用:通信中调制与解调,频分复用
将频谱搬到不同的位置
10. 时域积分性质
- 性质:若
f
(
t
)
↔
F
(
ω
)
,
则
F
(
0
)
=
0
时,
∫
−
∞
t
f
(
τ
)
d
τ
↔
F
(
ω
)
j
ω
f(t)\leftrightarrow F(\omega), 则 F(0)=0时,\int_{-\infty}^t f(\tau)d\tau\leftrightarrow\frac{F(\omega)}{j\omega}
f(t)↔F(ω),则F(0)=0时,∫−∞tf(τ)dτ↔jωF(ω)
F ( 0 ) ≠ 0 时, ∫ − ∞ t f ( τ ) d τ ↔ π F ( 0 ) δ ( ω ) + F ( ω ) j ω \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad F(0)\neq0时,\int_{-\infty}^t f(\tau)d\tau\leftrightarrow\pi F(0)\delta(\omega)+\frac{F(\omega)}{j\omega} F(0)=0时,∫−∞tf(τ)dτ↔πF(0)δ(ω)+jωF(ω)
也可以记作: F ( ω ) ⋅ [ 1 j ω + π δ ( ω ) ] F(\omega)\cdot[\frac{1}{j\omega}+\pi\delta(\omega)] F(ω)⋅[jω1+πδ(ω)] - 证明:
∫ − ∞ ∞ [ ∫ − ∞ t f ( τ ) d τ ] e − j ω t d t \int_{-\infty}^{\infty}[\int_{-\infty}^tf(\tau)d\tau]e^{-j\omega t}dt ∫−∞∞[∫−∞tf(τ)dτ]e−jωtdt
= ∫ − ∞ ∞ [ ∫ − ∞ ∞ f ( τ ) u ( t − τ ) d τ ] e − j ω t d t =\int_{-\infty}^{\infty}[\int_{-\infty}^{\infty}f(\tau)u(t-\tau)d\tau]e^{-j\omega t}dt =∫−∞∞[∫−∞∞f(τ)u(t−τ)dτ]e−jωtdt
= ∫ − ∞ ∞ f ( τ ) [ ∫ − ∞ ∞ u ( t − τ ) e − j ω t d t ] d τ =\int_{-\infty}^{\infty}f(\tau)[\int_{-\infty}^{\infty}u(t-\tau)e^{-j\omega t}dt]d\tau =∫−∞∞f(τ)[∫−∞∞u(t−τ)e−jωtdt]dτ(交换积分顺序,先t后 τ \tau τ,即先求时移的单位阶跃信号的傅里叶变换)
= ∫ − ∞ ∞ f ( τ ) ( π δ ( ω ) + 1 j ω ) e − j ω τ d τ =\int_{-\infty}^{\infty}f(\tau)(\pi\delta(\omega)+\frac{1}{j\omega})e^{-j\omega\tau}d\tau =∫−∞∞f(τ)(πδ(ω)+jω1)e−jωτdτ(利用时移特性)
= ( π δ ( ω ) + 1 j ω ) ∫ − ∞ ∞ f ( τ ) e − j ω τ d τ =(\pi\delta(\omega)+\frac{1}{j\omega})\int_{-\infty}^{\infty}f(\tau)e^{-j\omega\tau}d\tau =(πδ(ω)+jω1)∫−∞∞f(τ)e−jωτdτ(对积分变量 τ \tau τ而言 ω \omega ω为常数,移到积分外)
= ( π δ ( ω ) + 1 j ω ) F ( ω ) =(\pi\delta(\omega)+\frac{1}{j\omega})F(\omega) =(πδ(ω)+jω1)F(ω)(时域相卷,频域相乘)





















 7821
7821

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








