文章目录
1. 冲激函数
F ( ω ) = ∫ − ∞ ∞ δ ( t ) e − j ω t d t = 1 F(\omega) = \int_{-\infty}^{\infty}\delta(t)e^{-j\omega t}dt=1 F(ω)=∫−∞∞δ(t)e−jωtdt=1
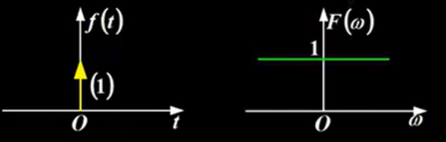
∙ δ ( t ) 看作 τ ∗ 1 τ \bullet \delta(t)看作\tau*\frac{1}{\tau} ∙δ(t)看作τ∗τ1的矩形脉冲（傅里叶变换是Sa函数）， τ → 0 \tau\to0 τ→0时， B ω → ∞ B_\omega\to\infty Bω→∞（零点趋于无穷）
∙ \bullet ∙冲激函数积分是有限值，可以用公式求
最低0.47元/天 解锁文章
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
