拟凸函数与拟凹函数

最新推荐文章于 2023-02-24 05:26:37 发布

使君杭千秋

最新推荐文章于 2023-02-24 05:26:37 发布

阅读量8.4k

点赞数 2

分类专栏：凸优化

本文链接：https://blog.youkuaiyun.com/hyl1181/article/details/111569234

版权

62 篇文章

订阅专栏

1.定义

函数 $f:R^n\rightarrow R$ 称为拟凸函数，当且仅当其定义域和所有下水平集 $S_\alpha =\left \{ x\in dom(f) |f(x)\leq \alpha \right \},\alpha \in R$ ，都是凸集。

2.Jensen不等式

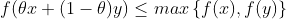若f为拟凸函数，当且仅当dom(f)是凸集，且 $\forall x,y\in dom(f),\forall \theta \in[0,1],$ 有 $f(\theta x+(1-\theta)y)\leq max\left \{ f(x),f(y) \right \}$ 。

3.一阶条件

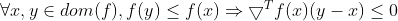设函数 $f:R^n\rightarrow R$ 可微，则函数f是拟凸函数的充要条件，dom(f)是凸集，且 $\forall x,y\in dom(f),f(y)\leq f(x)\Rightarrow \bigtriangledown ^Tf(x)(y-x)\leq 0$ 。

4.二阶条件

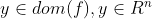假设函数 $f:R^n\rightarrow R$ 二阶可微。如果函数f为拟凸函数，则对任意的 $y\in dom(f),y\in R^n$ 有： $y^{T} \nabla f(x)=0 \Rightarrow y^{T} \nabla^{2} f(x) y \geq 0$ ；

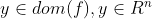如果对于任意 $y\in dom(f),y\in R^n$ ，函数f满足： $y^{T} \nabla f(x)=0=y^{T} \nabla^{2} f(x) y>0$ ，则函数f为拟凸函数。

5.连续函数 $f:R^n\rightarrow R$ 是拟凸的，当且仅当下述条件至少有一个成立

（1）f是非减的

（2）f是非增的

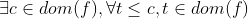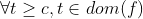（3） $\exists c\in dom(f),\forall t \leq c,t\in dom(f)$ ，f非增， $\forall t\geq c,t\in dom(f)$ ，f非减。

1.定义

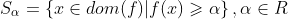函数 $f:R^n\rightarrow R$ 称为拟凹函数，当且仅当其定义域和所有上水平集 $S_\alpha =\left \{ x\in dom(f) |f(x) \geqslant \alpha \right \},\alpha \in R$ ，都是凸集。

2.Jensen不等式

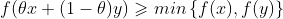若f为拟凹函数，当且仅当dom(f)是凸集，且 $\forall x,y\in dom(f),\forall \theta \in[0,1],$ 有 $f(\theta x+(1-\theta)y)\geqslant min\left \{ f(x),f(y) \right \}$ 。

3.一阶条件

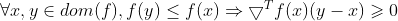设函数 $f:R^n\rightarrow R$ 可微，则函数f是拟凹函数的充要条件，dom(f)是凸集，且 $\forall x,y\in dom(f),f(y)\leq f(x)\Rightarrow \bigtriangledown ^Tf(x)(y-x)\geqslant 0$ 。

4.二阶条件

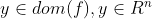假设函数 $f:R^n\rightarrow R$ 二阶可微。如果函数f为拟凹函数，则对任意的 $y\in dom(f),y\in R^n$ 有： $y^{T} \nabla f(x)=0 \Rightarrow y^{T} \nabla^{2} f(x) y \leqslant 0$ ；

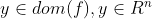如果对于任意 $y\in dom(f),y\in R^n$ ，函数f满足： $y^{T} \nabla f(x)=0=y^{T} \nabla^{2} f(x) y<0$ ，则函数f为拟凹函数。

5.连续函数 $f:R^n\rightarrow R$ 是拟凹的，当且仅当下述条件至少有一个成立

（1）f是非减的

（2）f是非增的

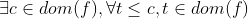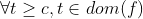（3） $\exists c\in dom(f),\forall t \leq c,t\in dom(f)$ ，f非减， $\forall t\geq c,t\in dom(f)$ ，f非增。