凸优化第三章凸函数作业题

最新推荐文章于 2023-05-17 13:19:02 发布

使君杭千秋

最新推荐文章于 2023-05-17 13:19:02 发布

阅读量3.6k

点赞数 2

分类专栏：凸优化

原文链接：https://blog.youkuaiyun.com/wangchy29/article/details/86561350

版权

凸优化专栏收录该内容

62 篇文章

订阅专栏

水平集

1)Some level sets of a function f are shown below. The curve labeled 1 shows $\left \{ x|f(x)=1 \right \}$ ,etc

Which of the following properties could f have?

由图像可看出f(x)的下水平集是凸集，故函数是拟凸函数，但不能由下水平集是凸集而判断函数是凸函数还是凹函数。而函数上水平集不是凸集，故函数f(x)不是拟凹函数。

2)Now consider the following function:

Which of the following properties could f have?

从图像函数下水平集不是凸集，已知凸函数的下水平集一定是凸集，所以函数f(x)不是凸函数，故其为凹函数。而上水平集是凸集，故函数f(x)是拟凹函数。

函数和上境图

1)The epigraph of a function f is a halfspace if and only if

函数的上境图是半空间，即下图，所以函数f(x)是一个仿射函数。

2)The epigraph of a function f is a convex cone if and only if

函数f(x)的上境图是一个凸锥，所以f(x)一定是凸函数，根据凸锥的定义： $\forall z,y\in C,\forall \theta_1 ,\theta _2\geq 0,\theta_1 z+\theta_2 y\in C$ ，

如上图，令 $\theta_2=0$ ，此时只看z的那条射线，可知 $\forall \theta_1\geqslant 0,\theta_1 z\in C$ ，因为上图是f(x)的上境图，故z的射线其实就是f(x)函数在那段区间的取值，这里假设z的射线对应的x区间为 $[x_1,+\infty ]$ ，所以 $\forall x \in[x_1,+\infty ],(x,f(x))$ 都在射线z上， $\forall \theta_1\geq 0,(\theta_1 x,f(\theta_1 x))$ 在射线z上，由锥的定义 $\forall \theta_1\geqslant 0,\theta_1 z\in C$ ，可知 $\forall \theta_1\geq 0,x\in [x_1,+\infty ],(\theta_1 x,\theta_1 f(x))\in z\Rightarrow \forall \theta_1\geq 0,x\in [x_1,+\infty ],(\theta_1 x,\theta_1 f(x))=(\theta_1 x,\theta_1 f(x))$

同理可证在射线y上 $\forall \theta_1\geq 0,x\in [-\infty ,x_1 ],(\theta_1 x,\theta_1 f(x))=(\theta_1 x,\theta_1 f(x))$

综上可知 $\forall x,\forall a\geq 0,f(ax)=af(x)$

3)The epigraph of a function f is a polyhedron if and only if

因为多面体是凸集，所以f(x)的上境图是凸集，所以f(x)是凸函数。根据定义多面体是多个不等式和等式解集，几何上是有限个半空间和超平面的交集，半空间是仿射函数的上境图，多个半空间的交集，即可以是分段仿射函数的上境图。

凸性和拟凸性

For each of the following functions, determine whether it is convex, concave, quasiconvex, or quasiconcave. (Check all that apply.)

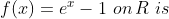
1) $f(x)=e^x-1 \, \, on \, R\, \, is$

证明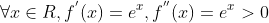： $\forall x \in R,f^{'}(x)=e^x,f^{''}(x)=e^x> 0$ ，故f(x)是凸函数。

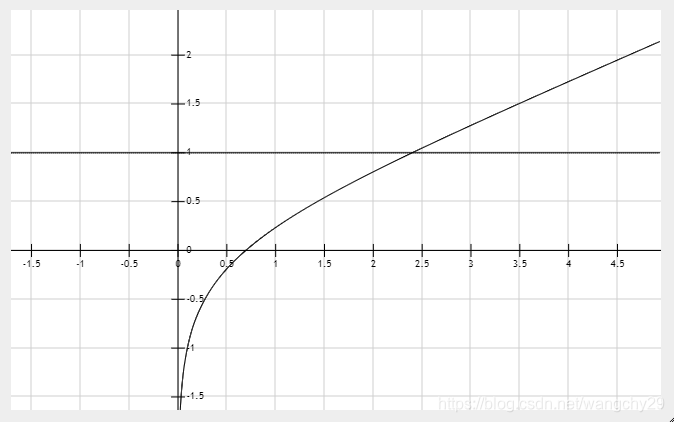
上图是函数f(x)的图像，可看出其上水平集合下水平集均为凸集，故函数f(x)既是拟凸函数又是拟凹函数。

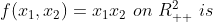
2) $f(x_1,x_2)=x_1x_2\, \, on \, \, R^2_{++}\, \, is$

证明：根据海瑟矩阵

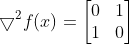$\bigtriangledown ^2f(x)=\begin{bmatrix} 0 &1 \\ 1 & 0 \end{bmatrix}$ 可判断函数集不是凸函数也不是凹函数。

看其下水平集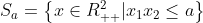： $S_a=\left \{ x \in R^2_{++}|x_1x_2\leq a \right \}$

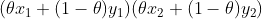
$\forall y,x\in R^2_{++},\forall \theta \in[0,1],\theta x+(1-\theta)y=(\theta x_1+(1-\theta)y_1,\theta x_2+(1-\theta)y_2)$

即

$(\theta x_1+(1-\theta)y_1)(\theta x_2+(1-\theta)y_2)$

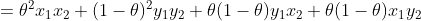
$=\theta ^2x_1x_2+(1-\theta)^2y_1y_2+\theta(1-\theta)y_1x_2+\theta(1-\theta)x_1y_2$

$=\theta ^2x_1x_2+(1-\theta)^2y_1y_2+\theta(1-\theta)y_1x_2+\theta(1-\theta)x_1y_2-\theta x_1x_2+\theta x_1x_2+(1-\theta)y_1y_2-(1-\theta)y_1y_2$

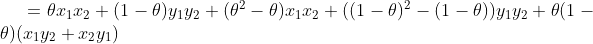
$=\theta x_1x_2+(1-\theta)y_1y_2+(\theta ^2-\theta)x_1x_2+((1-\theta)^2-(1-\theta))y_1y_2+\theta(1-\theta)(x_1y_2+x_2y_1)$

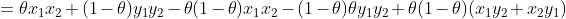
$=\theta x_1x_2+(1-\theta)y_1y_2-\theta (1-\theta)x_1x_2-(1-\theta)\theta y_1y_2+\theta(1-\theta)(x_1y_2+x_2y_1)$

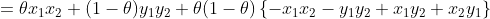
$=\theta x_1x_2+(1-\theta)y_1y_2+\theta (1-\theta)\left\{-x_1x_2- y_1y_2+x_1y_2+x_2y_1\right\}$

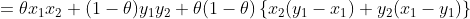
$=\theta x_1x_2+(1-\theta)y_1y_2+\theta (1-\theta)\left\{x_2(y_1-x_1) +y_2(x_1-y_1)\right\}$

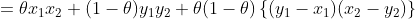
$=\theta x_1x_2+(1-\theta)y_1y_2+\theta (1-\theta)\left\{(y_1-x_1) (x_2-y_2)\right\}$

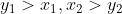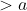当 y_1> x_1,x_2>y_2 时，上式 > a ，所以下水平集不是凸集

而上水平集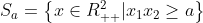 $S_a=\left \{ x \in R^2_{++}|x_1x_2\geq a \right \}$ 是凸集，故函数是拟凹函数。

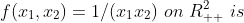
3) $f(x_1,x_2)=1/(x_1x_2)\, \, on \, \, R^2_{++}\, \, is$

证明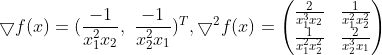： $\bigtriangledown f(x)=( \frac{-1}{x_1^2x_2},\ \frac{-1}{x_2^2x_1})^T,\bigtriangledown^2 f(x)=\begin{pmatrix} \frac{2}{x_1^3x_2} &\frac{1}{x_1^2x_2^2} \\ \frac{1}{x_1^2x_2^2}& \frac{2}{x_2^3x_1} \end{pmatrix}$ 正定，所以函数f(x)是凸函数，所以函数f(x)也是拟凸函数。

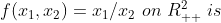
4) $f(x_1,x_2)=x_1/x_2\, \, on \, \, R^2_{++}\, \, is$

证明：

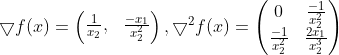$\bigtriangledown f(x)=\begin{pmatrix} \frac{1}{x_2}, & \frac{-x_1}{x_2^2} \end{pmatrix},\bigtriangledown ^2f(x)=\begin{pmatrix} 0 & \frac{-1}{x_2^2}\\ \frac{-1}{x_2^2} & \frac{2x_1}{x_2^3} \end{pmatrix}$ ，既不是半正定也不是半负定，所以既不是凸函数也不是凹函数。

看其下水平集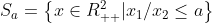 $S_a=\left \{ x \in R^2_{++}|x_1/x_2\leq a \right \}$

$\forall x,y \in S_a,x=(x_1,x_2),y=(y_1,y_2),\forall \theta \in [0,1],(\theta x+(1-\theta) y)$

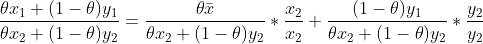
$\frac{\theta x_1 +(1-\theta) y_1}{\theta x_2+(1-\theta) y_2}=\frac{\theta \bar{x}}{\theta x_2+(1-\theta) y_2}*\frac{x_2}{x_2}+\frac{(1-\theta)y_1}{\theta x_2+(1-\theta) y_2}*\frac{y_2}{y_2}$

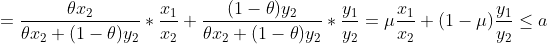
$=\frac{\theta x_2}{\theta x_2+(1-\theta) y_2}*\frac{x_1}{x_2}+\frac{(1-\theta) y_2}{\theta x_2+(1-\theta) y_2}*\frac{y_1}{y_2}=\mu \frac{x_1}{x_2}+(1- \mu)\frac{y_1}{y_2}\leq a$

所以上水平集是凸集，所以函数是拟凸函数。同理可证下水平集也是凸集，函数是拟凹函数。

一般向量组成规则

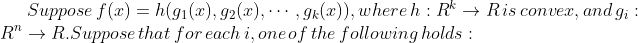
$Suppose\, f(x)=h(g_1(x),g_2(x),\cdots ,g_k(x)),where\, h:R^k\rightarrow R \, is\, convex,and\, g_i:R^n\rightarrow R.Suppose\, that\, for\, each\, i,one\, of\, the\, following\, holds:$

h is nondecreasing in the ith argument, and g_i is convex

h is nonincreasing in the ith argument, and g_i is concave

g_i is affine.

Fill in the blanks in the proof below to show that f is convex. (This composition rule subsumes all the ones given in the book and is the one used in software systems such as CVX.) Assume that 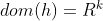dom(h)=R^k ; the result also holds in the general case when the monotonicity conditions above are imposed on 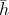$\bar{h}$ , the extended-valued extension of h.

proof:

$Fix\, x,y,and\, \theta \in[0,1],and\, let\, z=\theta x+(1-\theta)y.Let's\, re-arrange\, the\, indexes\, so\, that\, g_i\, is\, affine\, for\, i=1,\cdots p,g_i\, is\, convex\, for\, i=p+1,\cdots ,q,and\, g_i\, is\, concave\, for\, i=q+1,\cdots ,k.Therefore\, we\, have$

$g_i(z)(\, \, \, )\theta g_i(x)+(1-\theta)g_i(y),i=1,\cdots p$

$g_i(z)(\, \, \, )\theta g_i(x)+(1-\theta)g_i(y),i=p+1,\cdots q$

$g_i(z)(\, \, \, )\theta g_i(x)+(1-\theta)g_i(y),i=q+1,\cdots k$

The correct inequalities in the above equations are

根据仿射函数，凸函数和凹函数的定义，上述答案是显然的。

$\begin{eqnarray*} f(z) &=& h(g_1(z), g_2(z), \ldots, g_k(z))\\[0.2em] &\leq & h(\theta g_1(x)+ (1-\theta) g_1(y), \ldots, \theta g_k(x)+ (1-\theta) g_k(y)) \\[0.2em] &\leq & \theta h(g_1(x), \ldots, g_k(x)) + (1-\theta ) h(g_1(y), \ldots, g_k(y)) \\[0.2em] &=& \theta f(x) + (1-\theta) f(y). \end{eqnarray*}$

The second line holds since, for i=p+1,…,q, we have _ the ith argument of h, which is (by assumption) nondecreasing in the ith argument, and for i=q+1,…,k, we have _ the ith argument, and h is nonincreasing in these arguments. The third line follows from _.

The correct phrases that fill the blank spots are

共轭函数

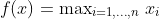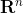What is the conjugate function of $f(x) = \mathrm{max}_{i=1,\dots,n}\ x_i$ on $\mathbf{R}^n$ ？

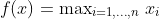根据共轭函数的定义： $f^*(y)=\underset{x\in dom(f)}{sup}(y^Tx-f(x))$ ，因为 $f(x) = \mathrm{max}_{i=1,\dots,n}\ x_i$ ，这里对 x_i 求偏导，当 $x_i=max\, x_i$ 时，得到

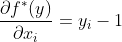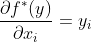$\frac{\partial f^*(y)}{\partial x_i}=y_i-1$ ，令其为0，得到 y_i=1 ，当 $x_i\neq max\, x_i$ 时， $\frac{\partial f^*(y)}{\partial x_i}=y_i$ ，令其为0得到 y_i=0 ，所以y是一个向量只在 $x_i=max\, x_i$ 的i分量为1，其他分量为0，所以选A。