矩阵结果与算法复杂性
Algorithm flop counts allow for very accurate and precise prediction of running time on a given computer.

About how long does a 1 Gflop computer take to solve a system of 100 linear equations with 100 variables?

About how long does a 1 Gflop computer take to solve 10 systems of of 100 linear equations with 100 variables, with the same coefficient matrix but 10 different right hand sides?

Since matrix multiplication is associative, the flop count for multiplying three or more matrices doesn't depend on the order in which you multiply them.

多个矩阵相乘,计算的顺序对浮点数运算次数有影响,比如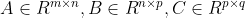
考虑计算ABC的两种顺序,
(1)先计算AB,再计算(AB)C,首先计算AB所需浮点计算次数为mp(2n-1),再计算(AB)C所需浮点计算次数为mq(2p-1),一共mp(2n-1)+mq(2p-1)=2mp(n+q)-m(p+q)
(2)先计算BC,再计算A(BC),首先计算BC所需浮点计算次数为nq(2p-1),再计算A(BC)所需浮点计算次数为mq(2n-1),一共nq(2p-1)+mq(2n-1)=2qn(m+p)-q(m+n)
求解已经因式分解的矩阵的线性方程组
Suppose 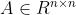 is lower triangular. The flop count for computing Ab is the same order as the flop count for computing
is lower triangular. The flop count for computing Ab is the same order as the flop count for computing 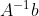 .
.

下三角矩阵的逆矩阵也是下三角矩阵,所以计算Ab和计算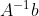 所需要浮点运算次数一样。
所需要浮点运算次数一样。
LU、Cholesky和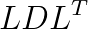 因式分解
因式分解
Suppose 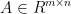 , and we need to compute x that minimizes
, and we need to compute x that minimizes 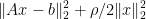 , where ρ>0.
, where ρ>0.
What is the flop count order when m≥n? (Provide your answer in terms of m and n. For example if you think the solution is m⋅n enter m*n in the answer box).
![]()
我是这样理解的:
目标函数写成
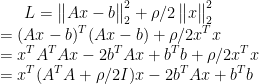
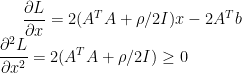
可知目标函数是凸函数,故令其一阶导数为0,得到

求解x,即求解此次方程组,记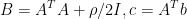 ,故方程组为
,故方程组为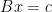
计算B所需要的浮点运算次数:(1)A^TA: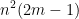 次 (2)
次 (2)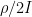 :0次(3)
:0次(3)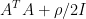 :只在对角线元素有加法,故n次
:只在对角线元素有加法,故n次
计算c的浮点运算: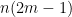
求解方程组: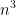
由于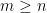 ,所以阶次是
,所以阶次是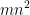
For m≤n, the flop count order is
![]()
这个答案我不理解。
Suppose m≥n, we have already solved the problem for one value of ρ, and now we want to compute the solution for k other values of ρ (this gives the so called regularization path). The flop count order for doing this is
![]()
对于这个答案我是这样理解的,首先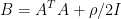 是对称正定矩阵,所以B是可以分解成
是对称正定矩阵,所以B是可以分解成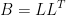 ,对一个
,对一个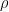 已经计算完了c,B 并求得了x值,所以已经求得了B 的分解,然后对于不同的
已经计算完了c,B 并求得了x值,所以已经求得了B 的分解,然后对于不同的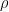 值,B只改变对角线上的元素,所以对于其他的
值,B只改变对角线上的元素,所以对于其他的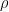 值,B的分解应该不再需要
值,B的分解应该不再需要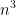 ,而是n,然后分解以后的计算量阶次是
,而是n,然后分解以后的计算量阶次是 ,k个不同的
,k个不同的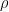 值,则需要
值,则需要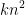 阶次的计算量。
阶次的计算量。
分块消元和Schur补
Suppose you wish to solve the following set of linear equations
![\left[ \begin{array}{ll} A_{11} & A_{12} \\ A_{21} & A_{22} \end{array} \right] \left[ \begin{array}{l} x_1 \\ x_2 \end{array} \right] = \left[ \begin{array}{l} b_1 \\ b_2 \end{array} \right]](https://i-blog.csdnimg.cn/blog_migrate/def96a90076936a7138c3e68bdd25df7.gif)
It is a good idea to eliminate 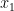 to solve the equations if
to solve the equations if

What is the computational complexity (order) of computing the Schur complement of the block 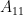 in the matrix
in the matrix
![\left[ \begin{array}{ll} A_{11} & A_{12} \\ A_{21} & A_{22} \end{array} \right]](https://i-blog.csdnimg.cn/blog_migrate/9855e61eb59e4618adb00434a0240123.gif)
with  ,
, 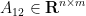 and
and 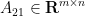 , given that the cost to factor a square matrix of size n is f and the cost to back solve a square matrix of size n is s?
, given that the cost to factor a square matrix of size n is f and the cost to back solve a square matrix of size n is s?
Your expression should only involve the symbols f, s, n and m.
![]()
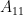 的Schur补为:
的Schur补为: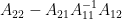 ,首先对
,首先对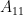 分解需要f,再计算
分解需要f,再计算 对应
对应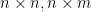 ,需要ms,在计算
,需要ms,在计算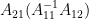 ,对应
,对应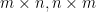 。需要
。需要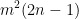 ,减法需要
,减法需要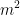 ,一共
,一共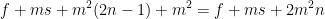 ,复杂度为
,复杂度为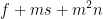 。
。
来源:https://blog.youkuaiyun.com/wangchy29/article/details/87906162
























 313
313

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








