9.2 下降方法
下降方法将产生一个优化点列 其中
其中 ,且
,且 。
。 是一个向量表示步径或搜索方向。标量
是一个向量表示步径或搜索方向。标量 被称为第k次迭代的步长。
被称为第k次迭代的步长。
方法的思想:只有 不是最优解,就找一个比
不是最优解,就找一个比 更好的点。
更好的点。
由目标函数凸性可知(一阶特征)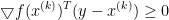 ,可知
,可知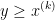 时,
时,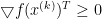 ,于是可知
,于是可知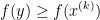 ,而在下降方法中显然
,而在下降方法中显然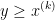 ,而且要求
,而且要求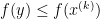 ,故下降方法中的搜索方向必须满足
,故下降方法中的搜索方向必须满足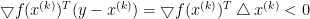 ,即它和负梯度放心的夹角必须是锐角。这样的方向为下降方向。
,即它和负梯度放心的夹角必须是锐角。这样的方向为下降方向。
下降方法:确定下降方向 ,然后选择步长t,其一般框架如下:
,然后选择步长t,其一般框架如下:
给定初始点
重复执行
- 确定下降方向

- 直线搜索:选择步长
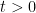
- 修改:
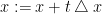
直到终止条件被满足
搜索方法类型
精确直线搜索
通过沿着射线优化f而确定t值:
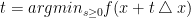
如果此问题的求解成本低于计算搜索方向的成本,则问比较适合用精确直线搜索。
回溯直线搜索
一种非精确直线搜索方法:沿着射线近似优化f而确定t值,即只有f有“足够的”的减少即可
算法:
- 给定f在
 处的下降方向
处的下降方向 ,参数
,参数 - t:=1
- 如果
,令
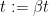
由于 是下降方向,
是下降方向,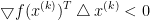 ,所以只要t足够小,
,所以只要t足够小,
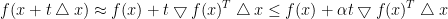
来源:https://blog.youkuaiyun.com/wangchy29/article/details/87966604
























 1380
1380

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








