8.6 分类
- 线性判别
- 非线性判别
线性判别
在线性判别中,寻找仿射函数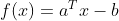 用以区分这些点,即
用以区分这些点,即
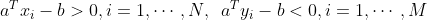
在几何意义上,即寻找分离两个点集的超平面。因为严格不懂呢过是对于a和b是齐次的,所以它们是可行的,当且仅当不严格不等式组:
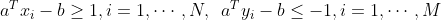
是可行的。
下图是两个点集即线性判别函数的例子。

鲁棒线性判别
如果两个集合可以倍被别,那么存在一个可以分离它们的仿射函数的多面体,于是我们可以从中选择某些稳健度量下最优的一个。例如,我们可以寻找给出在 上的正值和
上的正值和 上的负值之间最大可能“间距”的函数。
上的负值之间最大可能“间距”的函数。

如上图,两条虚线分别对应一个超平面,上侧的虚线对应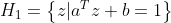 ,下侧的虚线对应
,下侧的虚线对应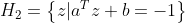 ,于是
,于是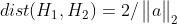 。
。
为了最大化间距,问题可以表述为:
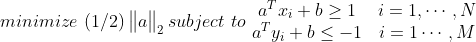
是一个关于a和b的二次规划问题。
最大间距问题的Langrange函数:
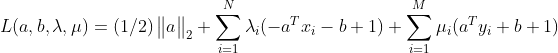
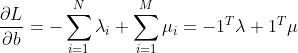
令其为0 ,得到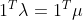
此时
对偶函数:
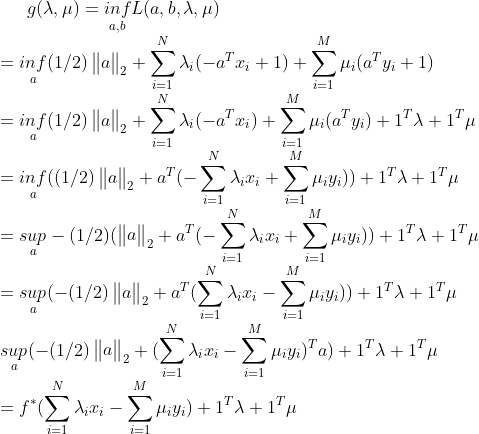
其中 是
是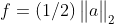 的共轭函数,故
的共轭函数,故

故对偶问题:
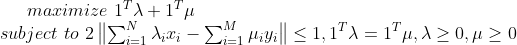
令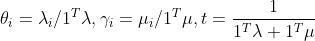
对偶问题等价于:
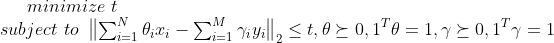
线性不可分的近似线性分类

如上图,两个集合线性不可分,此时没有一个仿射函数可以将两个集合分开,于是引入松弛量,即放宽约束,
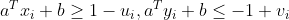
此时问题可以表述为:
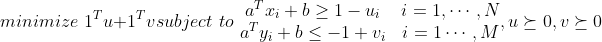
即寻找一个可以使点集更好的分类,同时最小化约束的放宽程度。
支持向量分类器
标准支持向量分类器定义为:
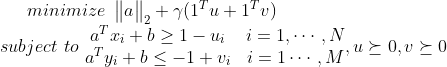
目标函数的第一项表示极大化间距,第二项对错分点的松弛。

如上图,实现是支持向量分类器得到的近似线性判别。
非线性判别
从函数子空间中寻找非线性函数,使得函数在一个集合中为正,另一个集合中为负。
可以定义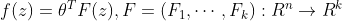
于是
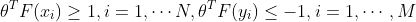
二次判别
取f(x)为二次函数: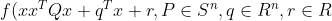
可以对P ,q,r增加约束以限制分类区间的形状。

多项式判别
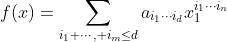

来源:https://blog.youkuaiyun.com/wangchy29/article/details/87881546
























 282
282

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








