Accumulation Degree POJ 3585（树形DP 二次扫描与换根法）

【例题】Accumulation Degree POJ 3585
有一个树形的水系，由N-1条河道和N个交叉点组成。我们可以把交叉点看作树中的节点，编号为1~N，河道则看作树中的无向边。每条河道都有一个容量，连x与y河道的容量记为c(x，y)。河道中单位时间流过的水量不能超过河道的容量。有一个节点是整个水系的发源地，可以源源不断地流出水，我们称之为源点。除了源点之外，树中所有度数为1的节点都是入海口，可以吸收无限多的水，我们称之为汇点。也就是说，水系中的水从源点出发，沿着每条河道，最终流向各个汇点。

在整个水系稳定时，每条河道中的水都以单位时间固定的水量流向固定的方向。除源点和汇点之外，其余各点不贮存水，也就是流入该点的河道水量之和等于从该点流出的河道水量之和。整个水系的流量就定义为源点单位时间发出的水量。

在流量不超过河道容量的前提下，求哪个点作为源点时，整个水系的流量最大，输出这个最大值。N≤2*10⁵。

输入
输入的第一行是整数T，表示测试数据的数量。
每个测试数据的第一行是正整数n。以下n-1行中的每一行包含由空格分隔的三个整数x，y，z，表示在节点x和节点y之间存在边缘，并且边缘的容量为z。节点编号从1到n。
所有元素都是非负整数，不超过200000.您可以假设测试数据都是树度量。

输出
对于每个测试用例，将结果输出到一行。

题目大意：

一棵树。
· 树的每个边都具有正边权，代表边的容量。
· 树中度为1的点被命名为出海口。
· 每个边的流量不能超过容量。
A（x）是将点x视作一个无线喷水机，表示点x可以流到其他（如果他也是出海口，则排除他）出海口的最大流量。
你的任务找一个点，使这个最佳最大流量，输出这个值。

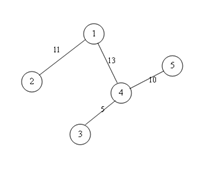
A（1）= 11 + 5 + 8 = 24
详细说明：
1->2 = 11
1->4->3 = 5
1->4->5 = 8（因为1-> 4的容量为13）
A（2）= 5 + 6 = 11
详细说明：
2->1->4->3 = 5
2->1->4->5 = 6
A（3）= 5
细节：
3->4->5 = 5
A（4）= 11 + 5 + 10 = 26
细节：
4->1->2 = 11
4->3 = 5
4->5 = 10
A（5）= 10
细节：
5->4->1->2 = 10
最大流量就是A(4)=26。

算法思想：
首先是暴力，枚举每一个点作为根，然后每次做一个树上DP，复杂度O(n2)。
枚举源点s，然后计算水系流量。把源点作为树根，整个水系就变成了一棵有根树，每条河道的方向也可以直接得出。
以树根为源点时，每个节点都只会从父节点获得水源，并流向它的子节点。每个节点的“流域”就是以该点为根的子树。这非常符合树形DP的应用场景----每棵子树都是一个“子问题”。
设Ds[x]表示在以x为根的子树中，把x作为源点，从x出发流向子树的流量最大是多少。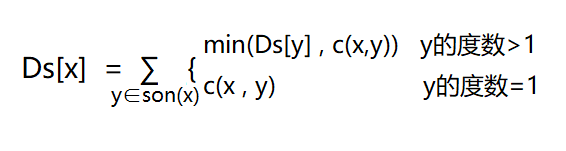
对于枚举的每个源点s，可以用树形DP在O（N）的时间内求出Ds数组，并用Ds[s]更新答案。所有，最终的时间复杂度位O（N²)。
下面的代码给出了一次树形DP的过程。在主函数中调用dp（s),完成后d[s]就是所求的Ds[s]。

void dp(int x) {
 v[x] = 1; // 访问标记
 d[x] = 0;
 for (int i = head[x]; i; i = Next[i]) { // 邻接表存储
  int y = ver[i];
  if (v[y]) continue;
  dp(y);
  if (deg[y] == 1) d[x] += edge[i]; // edge[i]保存c(x,y)
  else d[x] += min(d[y], edge[i]); 
 }
}

是一道“不定根”的树形DP问题，这类题目的特点是，给定一个树形结构，需要以每个结点为根进行一系列统计。我们一般通过两次扫描来求解此类问题：
1.第一次扫描，任选一个点为根，在“有根树”上执行一次树形DP。
2.第二次扫描，从刚才选出的根出发，对整棵树执行一次DFS，在每次递归前进行自上而下的推导，计算出“换根”之后的解。

用“二次扫描与换根法”代替源点的枚举，可以在O(N)的时间内解决整个问题。首先， 我们任选一个源点作为根节点， 记为root， 然后采用上面的代码进行一次树DP， 求出Droot数组，简记为D数组。
设F[x]表示把x作为源点， 流向整个水系， 流量最大是多少。对于根节点root显然有F[root] =D[root] 。
假设F[x]已被正确求出，考虑其子节点y，F[y]尚未被计算。F[y]包含两部分：
1.从y流向以y为根的子树的流量，已经计算并保存在D[y]中。
2.从y沿着到父节点x的河道，进而流向水系中其他部分的流量。

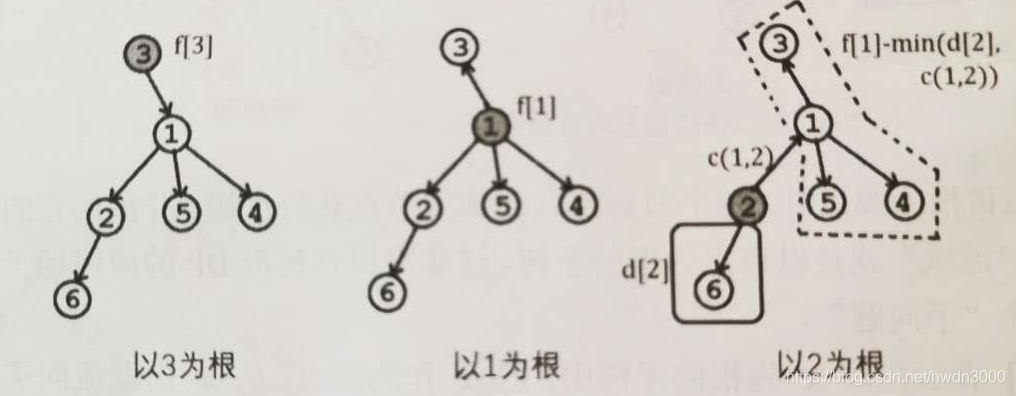
由题意可得，我们把x作为源点的总流量为F[x]，从x流向y的流量为min(D[y],c[x][y])，所以从x流向除y以外其他部分的流量就是二者之差F[x]−min(D[y],c[x][y])。于是，把y作为源点，先流到x，再流向其他部分的流量就是把这个“差”再与c[x][y]取较小值后的结果。

if(du[x]>1)→F[y]=D[y]+min( F[x]−min(D[y],c[x][y]) ，c[x][y] )

if(du[x]==1)→F[y]=D[y]+c[x][y]

F[y]就是把源点（树根）从x换成y后，流量的计算结果。这是一个由上而下的递推方程，我们通过一次DFS即可实现。

代码：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int d[200010], v[200010], f[200010], deg[200010];
int head[200010], ver[400010], edge[400010], Next[400010];
int n, T, tot, root, ans;

void add(int x, int y, int z) {
 ver[++tot] = y, edge[tot] = z, Next[tot] = head[x], head[x] = tot;
}

void dp(int x) {
 v[x] = 1; // 访问标记
 d[x] = 0;
 for (int i = head[x]; i; i = Next[i]) { // 邻接表存储
  int y = ver[i];
  if (v[y]) continue;
  dp(y);
  if (deg[y] == 1) d[x] += edge[i]; // edge[i]保存c(x,y)
  else d[x] += min(d[y], edge[i]); 
 }
}

void dfs(int x) {
 v[x] = 1;
 for (int i = head[x]; i; i = Next[i]) {
  int y = ver[i];
  if (v[y]) continue;
  if (deg[x] == 1) f[y] = d[y] + edge[i];
  else f[y] = d[y] + min(f[x] - min(d[y], edge[i]), edge[i]);
  dfs(y);
 }
}

int main() {
 cin >> T;
 while (T--) {
  tot = 1;
  cin >> n;
  tot = 1;
  for (int i = 1; i <= n; i++)
   head[i] = f[i] = d[i] = deg[i] = v[i] = 0;
  for (int i = 1; i < n; i++) {
   int x, y, z;
   scanf("%d%d%d", &x, &y, &z);
   add(x, y, z), add(y, x, z);
   deg[x]++, deg[y]++;
  }
  int root = 1; // 任选一个点为源点
  dp(root);
  for (int i = 1; i <= n; i++) v[i] = 0;
  f[root] = d[root];
  dfs(root);
  int ans = 0;
  for (int i = 1; i <= n; i++)
   ans = max(ans, f[i]);
  cout << ans << endl;
 }
}

邻接表的使用请读博文“邻接表”