1_Grassfire Algorithm_宾夕法尼亚大学机器人运动规划专项课程【学习笔记】

用0作为距离值标记目标节点，给所有距离目标节点1步的点标上1，距离2的标上2…以此类推，直至抵达起点。

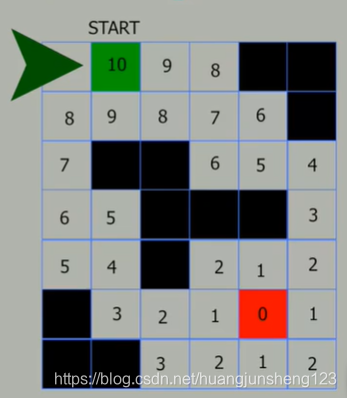
对于网格中的节点，标上的距离值代表的是从这个点走到目标点的最少步数。会发现这些数字从目标点向外辐射，就像火势蔓延一样，也即GrassFire名称的由来。

实际上，能够实现这种算法主要是依靠建立一个节点网络。每次在算法进行迭代时，就将第一个节点从列表中取出，再将其所有还未访问过的相邻点标记上当前点标记数值加1的值，然后把这个节点加入到这个列表的未尾(也就是作为终点)，下图所示概述了伪代码中的标记算法，这其实就是一个将BFS【Bread First Search】算法应用到图表中的简单例子，而其起点是例子中的终点。

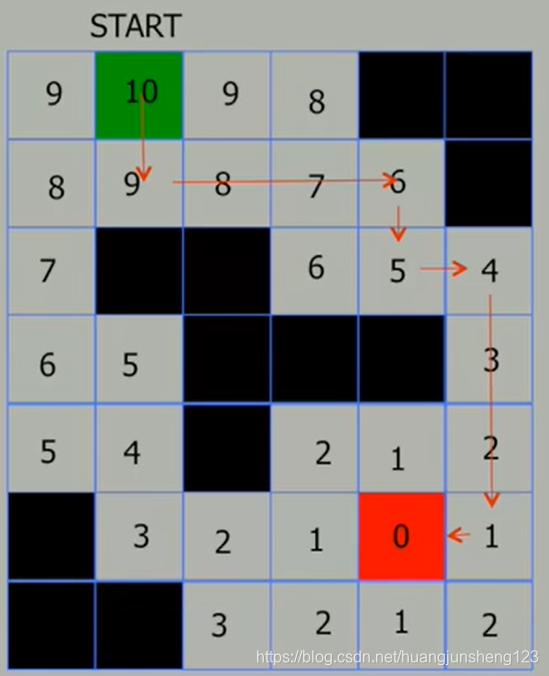
一旦起点被标记，便可以通过递归地移动到临近单元格而花费最小步数的方式，来构建起抵达目的地的最路径，这一页展示的是一个用这种方法构建的，从起点到终点的路径，注意如果目的地点的两个相邻点含有相同的距离标记值，你可以任意选择。这种情况会在抵达终点的最短路径不是唯一的时候出现。同样也可以通过将这个算法进行逆转，即从起始点开始然后向着终点进行迭代，并且会发现两种方法所规划出来的路径长度将相等。

下图是将“烧草算法”应用到另一个网格时的例子，在该例子中，若从目标点辐射的点无法进行迭代，算法便会终结。
对于这种情况，我们可以得出结论。因为问题起始点并未被标记，从起点到终点之间不存在可行路径

所以，烧草算法具有以下性质：完备性
若起点到终点的路径实际存在，就一定可以找到一个途径的边数最少的路径规划方案；
若路径并不存在，那么该算法将发现这种情况，并汇报给用户。

计算量
如果我们考虑在常规网格上运行“烧草算法”，每个网格单元最多被标记一次，更准确地来说，在网格上运行“烧草算法”所需要的计算量与节点数量呈线性相关。
假设我们考虑两个网格。一个是10x10，而另一个是20x20，大体上我们会知道后者花费的精力是前者的4倍，因为其含有四倍的节点数量。
我们可以使用完全相同的算法用作三维空间对机器人进行路径规划，如四旋翼，我们可以想象将机器人的工作空间看成三维网格，其中每个网格都县锐化的，然后使用“烧草算法”在网格的不同的两个单元之间进行路径规划。

如果我们将在100 * 100的二维网格上运行烧草算法的计算量 跟 在100 * 100 * 100的三维网格上运行的进行对比，发现后者的计算量应该比前者多大约100倍，或者这么说,若用同一台电脑运行后者花费时间是前者的100倍。进一步推广，想象路径规划发生在一个六维网格中，每边有100个元素的六维立方体将包含一个10的12次方个节点

结果表明，类似“烧草算法”的计算需求将随维度的增加而指数地增长。

感谢 B 站 up 主 Here_Kin 的翻译和分享！
【自制中英】宾夕法尼亚大学机器人专项课程二 运动规划 - Robotics:Motion and Planning