3_A* Algorithm_宾夕法尼亚大学机器人运动规划专项课程【学习笔记（附 A* Algorithm 代码获取链接）】

1. 课程笔记

前面提到的烧草算法（Grassfire Algorithm）和 Dijkstra 算法，都能找到最短路径，当路径不存在时，它们会报错；
然而由于执行过程中，两者都需要访问表中所有的节点，当节点数量庞大时，就会出现问题。

A* 算法通过探索式的代价函数来划分各条路径，探索各自的可能性，然后按照顺序来检查这些选择；
该算法和 Dijkstra 算法以及 Grassfire 算法很像，其升级之处在于保留正在探索的节点。当在简单网格上进行规划时，它跟前两种算法的执行过程都十分相似，因为所有相邻节点的距离都被检查过，两种算法都基于此节点到起点的距离来结束访问。

下边动图中，红色格子代表已经访问过的节点，蓝格子代表列表上即将要探索的节点，请注意，算法是如何激活各个点使其从起点均匀地在各个方向上传播的。可以发现， Dijkstra 和 Grassfire 算法基本上是均匀地探索所有方向，直到找到金色节点。

其实既然终点位置已经知晓，或许可以有别的办法使它做到更好，因为我们直到大概哪个方向距离终点更近。

在A* 算法中，引入了探索式距离【heuristic distance】的概念，即给定节点和目标节点之间的距离估计，然后利用这个信息将搜索方向引导到我们认为能更快到达目标的方向上.
在很多情况下，我们能够在某些信息基础上启发算法，使其更加高效，即在最短路径问题上使用启发式探索函数（H）

1.1 启发式探索函数

其会给定一个节点n并返回一个非负值，该值代表当前节点到终点的距离；

对于路径查找问题，经常使用单调的探索式函数，这意味着它们满足以下属性：

• H（终点）=0
• 对于图中相邻的两个任意节点x和y，H(x)<=H(y)+d(x,y)；其中，d(x,y)表示两个节点x和y之间边的长度。

不难发现，探索函数H(n)的作用是用来限制节点n和目标之间的距离。

这是两个常用于在二维网络上查找最佳路径的探索式函数，xn和yn表示节点在2D网格中的位置，xg和yg表示在同一网格中终点的坐标。

• 欧式距离（需要开方计算，运算量大）
• 曼哈顿距离（四连通，横竖）
• 切比雪夫距离（八连通，可以走斜步）

1.2 A* 算法伪代码

和 Dijkstra 算法结构非常相似，对于图表中的每个节点，将两个数值属性关联起来。
g值表示当前节点与起点之间的距离；
f值表示节点的g值和H(n)值的和，也就是当前节点与起点之间的距离以及估计从当前节点到终点之间距离的求和；
在每次迭代中，系统选择具有最小f值的节点，也就是说，它尽量选择很可能是在起点和终点之间最短路径上的节点。

一旦目标节点选定，对应它各个相邻节点的f值和g值就会进行相应的更新。换言之，每次迭代，我们尝试选择最有可能位于从起点到终点的最短路径上的节点，随后对选定节点的相邻节点进行更新，重复该过程直到到达终点或没有可以再更新的节点了。

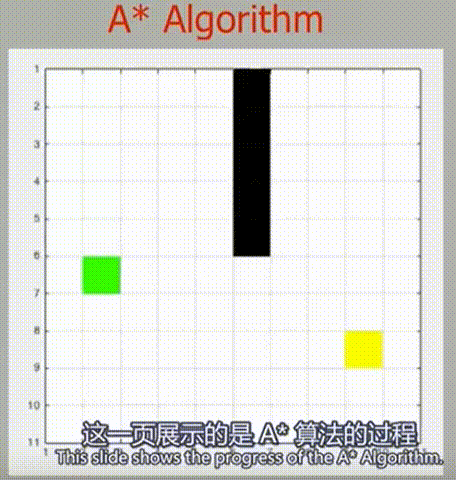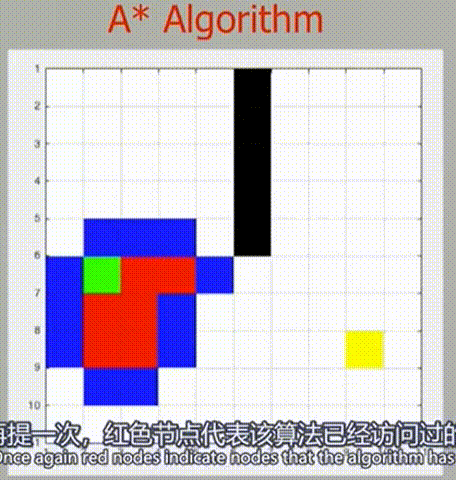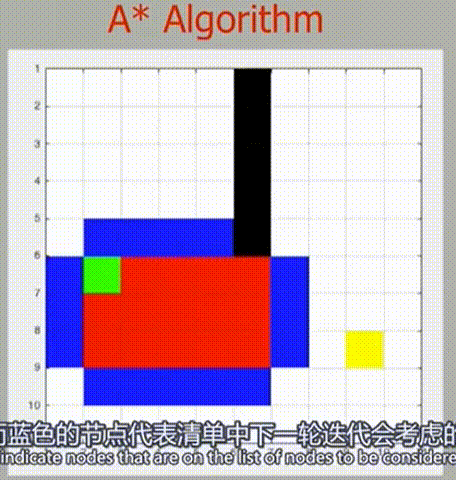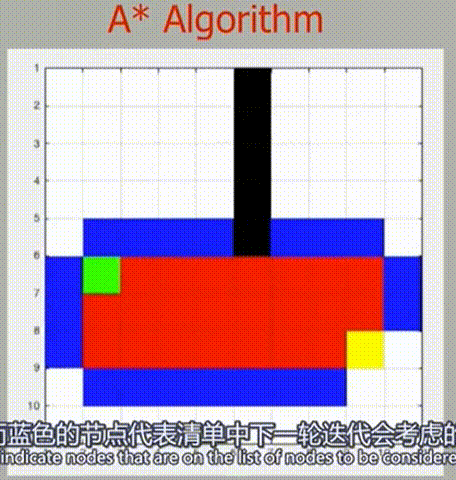可以发现 A* 算法往往按预期更直接地集中在更靠近目标的点上，比较一下和 Dijkstra 算法的性能 当 Dijkstra 算法在全方向上进行均匀探索时，A* 算法使用其探索函数将其探索方向集中到更靠近终点的方向上，所以 A* 算法能更加快速地找到抵达终点的路径。

即使在最坏的情况下，A* 算法的性能也与Dijkstra 算法相持平。

2. 其它参考学习资源推荐

感谢 B 站 up 主 Here_Kin 的翻译和分享！
【自制中英】宾夕法尼亚大学机器人专项课程二 运动规划 - Robotics:Motion and Planning

3. 算法复现效果

这是我完成的该课程对应的作业情况：
在该作业指定的地图中：

在我自定义的地图中：

4. 代码资源获取

点击获取对应的MATLAB代码资源