感谢:紫薯萝卜 https://zhuanlan.zhihu.com/p/76341809
论文:https://arxiv.org/abs/1712.00036
代码:https://github.com/KumarRobotics/msckf_vio
(很好,建议先看理论)整体讲解:http://www.xinliang-zhong.vip/msckf_notes/
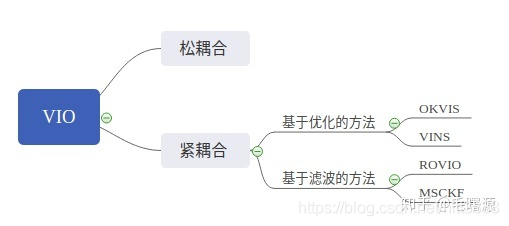
1. 什么是MSCKF?
MSCKF 全称 Multi-State Constraint Kalman Filter(多状态约束下的Kalman滤波器),是一种基于滤波的VIO算法,2007年由Mourikis在《A Multi-State Constraint Kalman Filter for Vision-aided Inertial Navigation》中首次提出。MSCKF在EKF框架下融合IMU和视觉信息,相较于单纯的VO算法,MSCKF能够适应更剧烈的运动、一定时间的纹理缺失等,具有更高的鲁棒性;相较于基于优化的VIO算法(VINS,OKVIS),MSCKF精度相当,速度更快,适合在计算资源有限的 嵌入式平台运行。在机器人、无人机、AR/VR领域,MSCKF都有较为广泛的运用,如Google Project Tango就用了MSCKF进行位姿估计。
VIO相对于VO的好处:
- 恢复尺度:IMU能够提供尺度信息(加速度计),解决单目VO的无法恢复尺度的问题。
- 应对纯旋转:在纯旋转的情况下,VO位姿解算会出现奇异,VIO可以利用IMU的陀螺仪(角速度计)来估计纯旋转运动。
- 应对短时间图像特征缺失:在出现图像过曝、图像过暗、环境纹理不足时,VO会无法工作,而VIO能在VO失效的情况下利用IMU积分来进行运动估计,能够应对短时间的视觉特征缺失(IMU积分越久累积误差会越大),比VO具有更高的鲁棒性。
- 精度更高:VIO融合了两种传感器的信息,位姿估计的精度要更高。
2. MSCKF相关学习资料
MSCKF开山之作
https://www-users.cs.umn.edu/~stergios/papers/ICRA07-MSCKF.pdf
数学理论相关资料
http://mars.cs.umn.edu/tr/reports/Trawny05b.pdf
http://www.iri.upc.edu/people/jsola/JoanSola/objectes/notes/kinematics.pdf
Li Mingyang老师的系列论文, MSCKF2.0,FEJ
时钟同步误差估计
https://intra.ece.ucr.edu/~mourikis/papers/Li2014IJRR_timing.pdf
能观性分析,FEJ
https://intra.ece.ucr.edu/~mourikis/papers/Li2013IJRR.pdf
Shelly(TUM CVG)的硕士论文,IPhone上跑MSCKF,实现步骤很详细
https://vision.in.tum.de/_media/spezial/bib/shelley14msc.pdf
Vijay Kumar实验室在github上开源的双目MSCKF和配套论文
https://github.com/KumarRobotics/msckf_vio
https://github.com/KumarRobotics/msckf_vio
3. MSCKF核心思想
MSCKF的目标是解决EKF-SLAM的维数爆炸问题。传统EKF-SLAM将特征点加入到状态向量中与IMU状态一起估计,当环境很大时,特征点会非常多,状态向量维数会变得非常大。MSCKF不是将特征点加入到状态向量,而是将不同时刻的相机位姿(位置 P和姿态四元数Q )加入到状态向量,特征点会被多个相机看到,从而在多个相机状态(Multi-State)之间形成几何约束(Constraint),进而利用几何约束构建观测模型对EKF进行update。由于相机位姿的个数会远小于特征点的个数,MSCKF状态向量的维度相较EKF-SLAM大大降低,历史的相机状态会不断移除,只维持固定个数的的相机位姿(Sliding Window),从而对MSCKF后端的计算量进行限定。
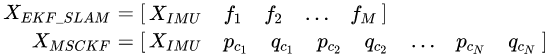
3.1 IMU状态向量与INS
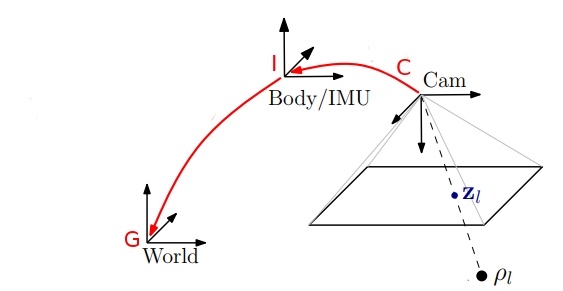
MSCKF本质是一个EKF,介绍MSCKF之前,我们先介绍一下INS(Inertial Navigation System)中的IMU状态EKF估计,INS中IMU的状态向量为
![]()
其中
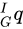 为单位四元数,表示从世界系(
为单位四元数,表示从世界系( 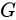 系)到IMU坐标系(
系)到IMU坐标系( 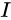 系)的旋转 //坐标系之间的转换矩阵有三种意思
系)的旋转 //坐标系之间的转换矩阵有三种意思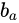 为加速度计accelerator的bias
为加速度计accelerator的bias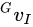 为IMU在G系下的速度
为IMU在G系下的速度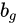 为陀螺仪gyroscope的bias
为陀螺仪gyroscope的bias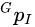 为IMU在G系下的位置
为IMU在G系下的位置
INS的EKF步骤为:
- EKF预测:先利用传感器获得的观测加速度和观测角速度,可以对状态进行估计,显然,该步骤会使得估计的不确定度/协方差越来越大
- EKF更新:然后利用视觉观测构建观测模型,对状态向量的均值和协方差进行更新, 修正预测过程的累积误差,减少不确定度。
3.2 MSCKF中的观测模型 (认真理解,其与GPS/INS松组合的不同)
对于MSCKF来说,EKF预测步骤与INS一样,区别在EKF观测更新,需要用视觉信息来构建观测模型,从而对IMU预测的状态进行更新。INS中GPS可以直接给出位置 ![]() 的观测,而视觉通常只能提供多个相机之间相对位姿关系的约束。那观测模型要怎么构建呢?
的观测,而视觉通常只能提供多个相机之间相对位姿关系的约束。那观测模型要怎么构建呢?
视觉中,约束通常都是特征点到相机的重投影误差(空间中一个3D特征点根据相机的姿态和位置投影到相机平面,与实际观测的特征点之间的误差):

我们希望用这个重投影误差的约束等式来作为观测模型,但前提是需要知道特征点的3D坐标,而实际应用中特征点的3D坐标是未知的。
- EKF-SLAM的做法是将特征点加入到状态向量进行估计,但它的状态向量会随特征点的增多而变得非常大。
- MSCKF的做法是根据历史相机位姿和观测来三角化计算特征点的3D坐标。这又带来了一个问题:如何确保三角化的精度呢?如果三角化误差太大,那么观测模型就会不准,最终会使得VIO精度太差。MSCKF做法是当特征点跟踪丢失后再进行三角化,特征点跟丢表示该特征的观测不会再继续增加了,这时利用所有的历史观测三角化。所以MSCKF中观测更新的时机是特征点跟丢。
4. MSCKF算法步骤
MSCKF算法步骤如下:
- IMU积分:先利用IMU加速度和角速度对状态向量中的IMU状态进行预测,一般会处理多帧IMU观测数据。
- 相机状态扩增:每来一张图片后,计算当前相机状态并加入到状态向量中, 同时扩充状态协方差.
- 特征点三角化:然后根据历史相机状态三角化估计3D特征点
- 特征更新:再利用特征点对多个历史相机状态的约束,来更新状态向量。注意:这里不只修正历史相机状态,因为历史相机状态和IMU状态直接也存在关系(相机与IMU的外参),所以也会同时修正IMU状态。
- 历史相机状态移除:如果相机状态个数超过N,则剔除最老或最近的相机状态以及对应的协方差.
MSCKF状态propagation和update的流程如下图所示:
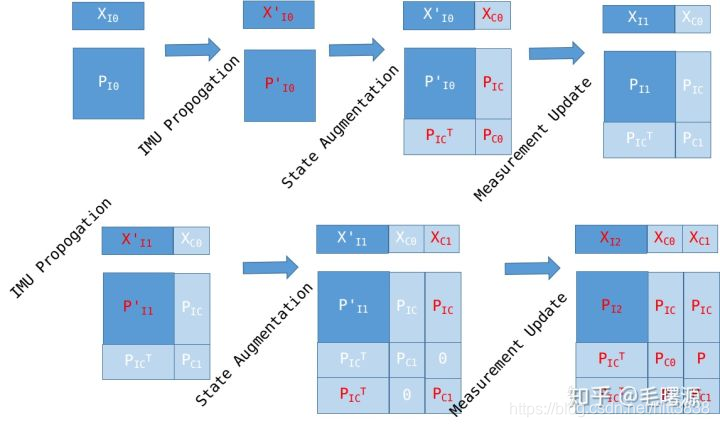
图中 X 表示状态向量, P 表示对应的协方差矩阵,红色表示当前步骤发生改变的量。
- 首先初始化状态向量和协方差
- 然后进行IMU积分,状态向量和协方差都发生改变
- 接着将新的相机状态加入到状态向量中,扩充协方差矩阵(新相机自身的协方差以及对
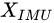 的协方差)
的协方差) - 进行观测更新,所有状态和协方差都会发生改变。(注意:第一次因为只有一个相机状态,形成不了重投影约束,所以第一次观测更新并不会做任何事情)
- 当相机状态个数超过限制时,删除最历史的一个相机状态及其对应的协方差项。
- 重复2-5。





















 3471
3471

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








