圆锥台(Frustum of Cone)

圆锥台是一种特殊的形状，用平行于圆锥底面的平面切割圆锥体后会形成。圆锥体是一个三维形状，具有圆形底面和顶点。因此，圆锥台是用平行于圆形底面的平面切割圆锥体的一部分形成的立体体。圆锥台不仅可用于圆锥体，也可用于不同类型的金字塔（四棱锥、三棱锥等）。

我们在日常生活中常见的一些圆台形状包括水桶、灯罩等等。本文将带您了解更多关于圆台的知识。

如果您喜欢此文章，请收藏、点赞、评论，谢谢，祝您快乐每一天。

什么是圆台？

Frustum 是一个拉丁词，意思是“碎片”，因此圆锥台是圆锥的实体碎片。用平行于圆锥底面的平面切割一个直圆锥，得到的形状称为圆锥台。下图展示了平面如何平行于圆锥底面切割圆锥，形成圆锥台。

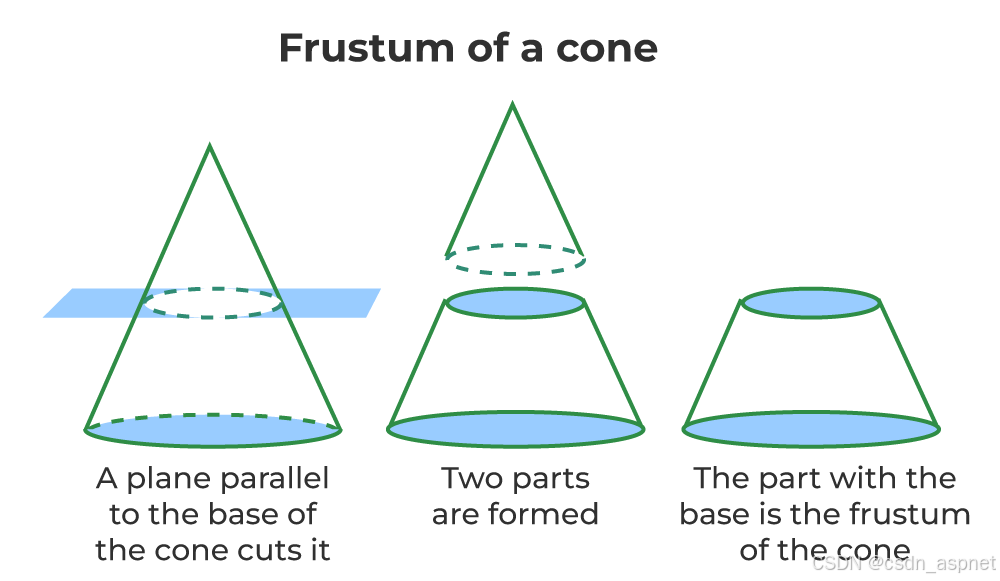
现在，圆锥台很容易定义为，

一个直圆锥被一个平行于其底面的平面截断后，截平面与底面之间的部分的形状叫圆台。 

圆台网

如果将一个三维（3D）图形切开，变成二维图形，则所得形状称为网格。我们可以假设，当网格以正确的方式折叠时，它就形成了所需的三维形状。下图展示了截头圆锥体的网格。

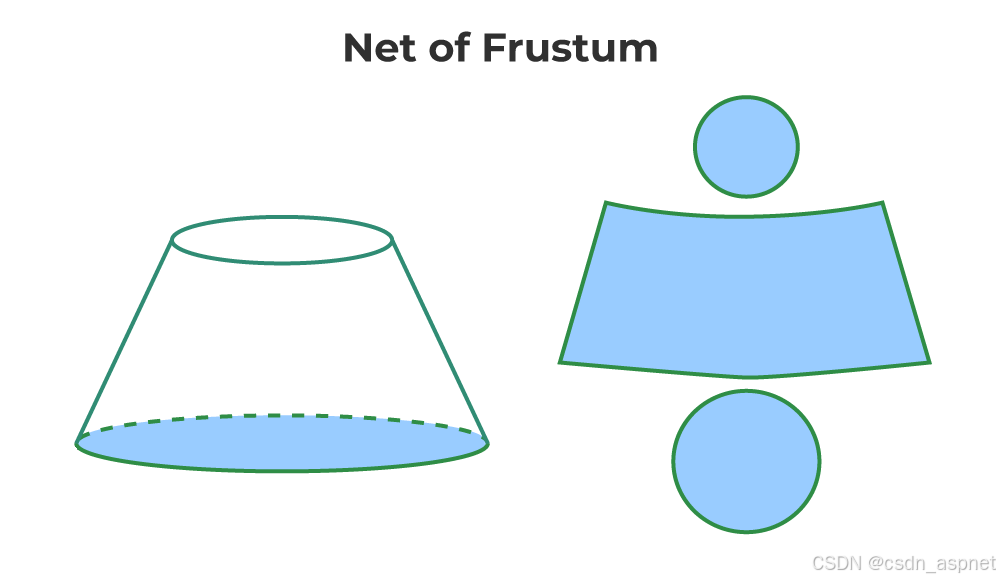
圆台的性质

圆锥台的性质与圆锥非常相似，圆锥台的一些重要性质是，

• 圆锥的底面原圆锥包含在圆锥台内但其顶点不包含在圆锥台内。
• 圆锥台的公式取决于其高度和两个半径（分别对应于顶底面）。
• 圆锥台的高是其两底面中心之间的垂直距离。

圆台体公式

圆台是我们日常生活中经常见到的一种形状，例如台灯、水桶等。圆台的重要公式是：

• 圆台体积
• 圆台的表面积

下面我们来详细了解一下这些公式，

圆台体积

圆台体是将圆锥体切成薄片，从大圆锥体中去掉一个小圆锥体。因此，要计算圆台体的体积，只需计算大圆锥体和小圆锥体体积之差即可。 

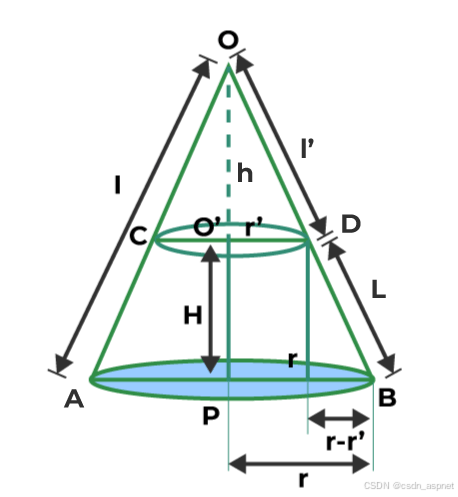
假设，

• 圆锥体的总高度为 H + h
• 总倾斜高度为 l' + L
• 完整圆锥的半径为r
• 切片圆锥的半径为 r'

由于圆锥的体积为 V = 1/3πr^2 h

完整圆锥的体积 V 1 = 1/3πr^2 (H+h)

小圆锥的体积 V 2 =1/3πr'^2 (h)

现在可以使用以下公式计算圆台体（V）的体积，

V = V 1 - V 2

V = 1/3πr² ( H+h)-1/3πr'² ( h)

V = 1/3π[r² ( H+h)-r'² (h) ] ...(1)

利用△OCD和△OAB三角形的相似性，可以写出： 

r / (H + h) = r' / h

r / r' = (H + h) / h

H + h = hr / r'

将 (H+h) 的值代入公式 (1) 中，简化为：

 V = 1/3π[r² ( rh/r')-r'² ( h)}

   = 1/3π[{hr^3 - hr'^3 } / r']...(2)

再次利用△OCD和△OAB的相似三角形性质，求出h的值

r / (H + h) = r' / h

r / r' = (H + h) / h

rh = (H + h)r'

rh = 小时' + 小时'

(r-r')h=Hr'

h = Hr' / (r -r')

将这些值代入公式（2），

V = 1/3π[{r^3 h - r^3 h} / r']

   = 1/3π[{r^3 - r'^3 }h / r']

   = 1/3π[{r^3 - r'^3 }{Hr' / (r - r')} / r']

   = 1/3πH(r^2 + r'^2 + rr')

因此，

圆台体积 = 1/3 πH(r^2 + r'^2 + rr')

圆台的表面积

圆台体的表面积可以通过完整圆锥体的表面积与较小圆锥体（从完整圆锥体中取出）的表面积之差来计算。圆台体的表面积可以通过下图计算，其中需要将曲面的表面积以及圆台体顶面和底面的表面积相加。

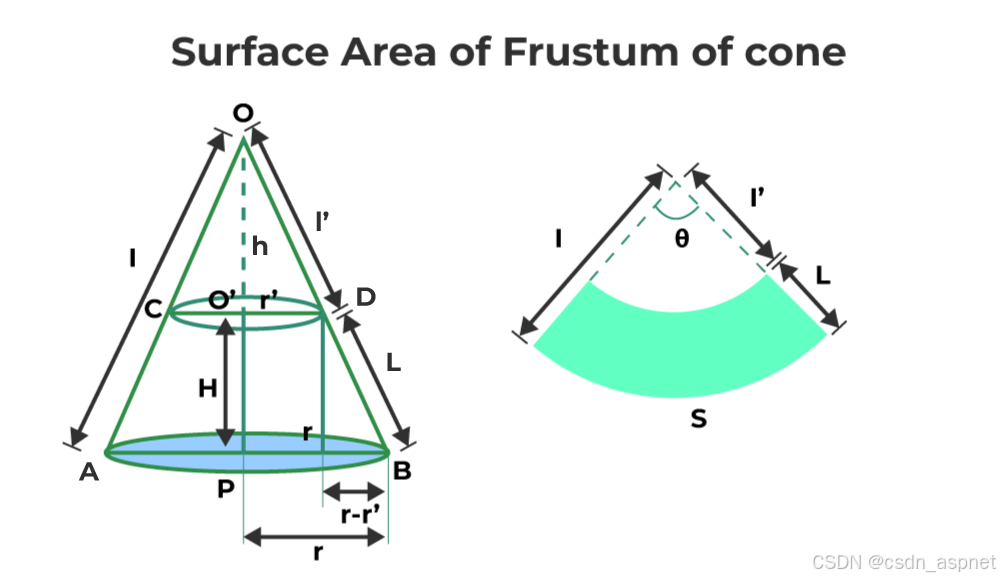
与圆锥台的体积类似，曲面面积也等于大圆锥与小圆锥的表面积之差。 

在上图中，三角形 OAB 和 OCD 相似。因此，根据相似性准则，可以得出：

l' / l = r' / r...(1)

因为 l' = l - L，因此，根据公式 (1)，

(l - L) / l = r' / r

经过交叉相乘后， 

lr-Lr = lr'

l(r - r') = Lr

l = Lr / (r - r')...(2)

完整圆锥的曲面面积=πrl

较小圆锥的曲面面积 = πr'l'

完整圆锥与小圆锥的曲面面积差=π（rl-r'l'）

因此，圆台的曲面面积（CSA）=πl（r-r'l'/l）

利用公式 (1) 代入上式中的 l'/l 值，简化为：

圆台的 CSA = πl (r - r'×r'/r) = πl (r^2 - r'^2 )/r

现在，代入公式 (2) 中的 l 值，并简化，

圆台的CSA = πlr/(r - r')× (r^2 - r'^2 )/r = πl (r + r')

因此，可以这样写，

圆台曲面面积=πl(r+r')

现在，让我们计算圆锥台顶部和底部底面的表面积，这样， 

半径为 r' = πr' 2的圆台顶面底面的表面积

半径为 r = πr 2 的圆台底部的表面积

所以，

圆台总表面积=圆台曲面面积+顶底面面积+底面面积

所以，

圆台总表面积= πl (r + r') + πr'^2 + πr^2 = πl (r + r') + π (r^2 + r'^2 ) 

 因此，圆台的总表面积为 = πl (r + r') + π (r^2 + r'^2 ) 

这个公式也可以写成， 

圆台的总表面积为 = πl (r^2 - r'^2 )/r + π (r^2 + r'^2 ) 

因此，我们可以这样写，

圆台体的总表面积 = πl(r + r') + π (r^2 + r'^2 ) 

或者

圆台总表面积 = πl (r^2 - r'^2 )/r + π (r^2 + r'^2 ) 

请注意，l 是较小圆锥的斜高，可以表示为 

L = √[H2 + (r - r')^2 ]

阅读更多

• 圆锥的体积
• 圆柱体体积
• 球体的体积

截头圆锥体的求解示例

例 1：求一个高 15 厘米、底面半径分别为 5 厘米和 8 厘米的圆台的体积。 

解决方案： 

使用上面研究的公式，可以写出，

V = 1/3 πH(r^2 + r'^2 + rr')

鉴于， 

H = 15 厘米
r'= 5 厘米
r = 8 厘米

V = 1/3 π15(8^2 + 5^2 + 40)

V = 5π(129)

V = 645π厘米^3

例 2：求一个高 10 厘米、底面半径分别为 4 厘米和 8 厘米的圆台的表面积和总表面积。 

解决方案： 

我们知道了截头锥体的表面积和总表面积的公式。我们需要代入所需的值。 

截头体的曲面面积 = πl(r+r')

其中，
L = √[H^2 + (R - r)^2 ]

已知，
H = 10 厘米
r = 4 厘米
R = 8 厘米 

计算L的值， 

L = √[10^2 + (8-4)^2 ]

  = √(100+16) = √(116)

截头锥体的曲面面积 = πL(R+r)

= π√(116)×(8+4)

= 48π√(29)

总表面积=截头锥体的曲面面积+两个底面的面积

= 48π√(29) + π(8)^2 + π(4)^2 

= 48π√(29) + 64π + 16π

= 48π√(29) + 80π 厘米²

例3：假设我们有一个开口的金属桶，其高度为50厘米，底部半径分别为10厘米和20厘米。求制作桶的金属板的面积。

解决方案： 

桶的形状是一个底部封闭的截头锥体。我们需要计算这个截头锥体的总表面积。 

已知
H = 50 厘米
r '= 10 厘米
r = 20 厘米

截头锥体的曲面面积 = πL(R+r)

L = √[H^2 + (r - r')^2 ]

L = √[50^2 + (20 - 10)^2 ]

  = √(2500+100) = √(2600)

  = √100(26) = 10√(26)

截头锥体的曲面面积 = πL(R+r)

= π10√(26)×(20+10)

= 300π√(26)

总表面积=截头锥体的曲面面积+两个底面的面积

= 300π√(26) + π(20)^2 + π(10)^2 

= 300π√(26) + 400π + 100π

= (300π√(26) + 500π) 厘米²

例 4： 设一个平截头体的高度为 6y，半径分别为 y 和 2y，求该平截头体的体积表达式。

解决方案： 

使用上面研究的公式， 

V = 1/3 πH(r^2 + r'^2 + rr')

鉴于， 

H = 6y 
r'= y 
r = 2y

V = 1/3 π6[(2y)^2 + (y)^2 + (y)(2y)]

V = 2πy( 7y^2 )

V = 14πy^3单位^3

如果您喜欢此文章，请收藏、点赞、评论，谢谢，祝您快乐每一天。