勾股定理公式

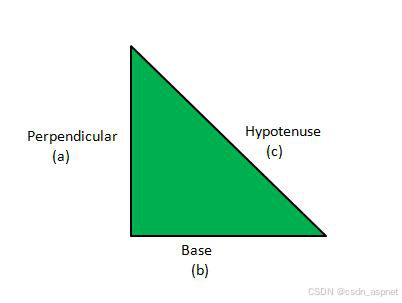
勾股定理，又称毕达哥拉斯定理，可以定义为直角三角形三条边（斜边、底边、垂线）之间的关系。该定理指出，两条短边（底边和垂线）的平方和等于最长边（斜边）的平方。

该定理以公元前 570 年左右出生的希腊哲学家毕达哥拉斯的名字命名。

如果您喜欢此文章，请收藏、点赞、评论，谢谢，祝您快乐每一天。

勾股定理公式

a^2 + b^2 = c^2​

这里 c 表示斜边的长度，a 和 b 表示垂线和底边的长度。所以，斜边^2 = 垂线^2 + 底边^2

例：取一个直角三角形，其边长为3，4，5，现证明勾股定理。

解决方案

两个小边的平方和 = 3^2 + 4^2 = 25

最长边的平方 = 5^2 = 25

因此我们可以看到

两条短边的平方和=最长边的平方 25 = 25

勾股定理显示了直角三角形边之间的关系，因此如果缺少任何边的长度，都可以使用勾股定理来计算。

如果已知 a（垂线）和 b（底线）的长度，则可以使用以下公式计算 c 的长度：

c = √( a^2 + b^2 )

同样，如果缺少 a 和 b，也可以计算出来。

示例问题

问题 1：求底边为 6 厘米、高为 8 厘米的直角三角形的斜边？

回答： 

利用勾股定理，a^2 + b^2 = c^2

所以 6^2 + 8^2 = c^2 

因此 c = √(36 + 64)

          c = √100

          c = 10厘米

问题 2：判断给定的三角形是否为直角三角形，边长为 6、8、12？

回答： 

直角三角形遵循勾股定理，所以让我们检查一下。

两条短边的平方和应该等于最长边的平方

所以 6^2 + 8^2一定等于 12^2

但 36 + 64 =100，而 12^2 = 144

因此它不是直角三角形，因为它不满足勾股定理。

问题 3：求斜边为 13 厘米、高为 12 厘米的直角三角形的底边？

回答： 

利用勾股定理，a^2 + b^2 = c^2

a（垂直线）= 12，c（斜边）= 13，求b（底边）

所以 b = √( c^2 - a^2 )

因此 b = √(169 - 144)

           b = √25

           b = 5厘米

问题 4：求斜边为 25 厘米、底边为 7 厘米的直角三角形的垂直线？

回答：

利用勾股定理，a^2 + b^2 = c^2

b（底边）= 7，c（斜边）= 25，求a（垂直线）

所以 a = √( c^2 - b^2 )

因此 a = √(625 - 49)

          a = √576

          a = 24厘米

问题 5：判断给定的三角形是否为直角三角形，边长分别为 10、24、26？

回答： 

直角三角形遵循勾股定理，所以让我们检查一下。

两条短边的平方和应该等于最长边的平方

所以 10^2 + 24^2一定等于 26^2

100 + 576 = 676 等于 26^2 = 676

因此，给定的三角形是直角三角形，因为它满足勾股定理。

如果您喜欢此文章，请收藏、点赞、评论，谢谢，祝您快乐每一天。