JavaScript 圆台体积和表面积计算程序(Program for Volume and Surface area of Frustum of Cone)

 给定圆锥台的斜高、高度和半径，我们必须计算圆锥台的体积和表面积。

圆台

在几何学中，截头体是指立体（通常是圆锥或金字塔）被一个或两个平行平面截开的部分。如果我们用一个平行于其底面的平面截一个直圆锥，则该平面与底面之间的部分称为圆锥截头体。下图是一个直圆锥。

如果您喜欢此文章，请收藏、点赞、评论，谢谢，祝您快乐每一天。

直圆锥被平行于其底面的平面切割后，形成如下的截头体：

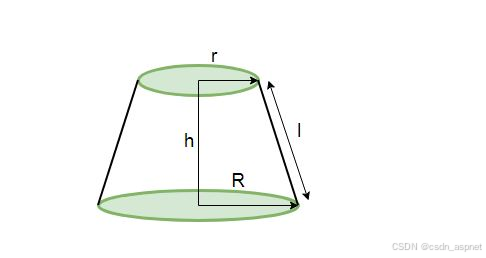
其底部为圆形，半径为 R，上部为圆形，半径为 r，高度为 h，斜高为 l

圆台体积：
体积 (V) = 1/3 * pi * h(r^2 + R^2 + r*R)
其中
r = 较小圆的半径
R = 较大圆的半径（或圆锥底面的半径）
h = 截头锥体的高度

圆台曲面面积：
曲面面积 (CSA) = pi * l(R + r)
其中
r = 较小圆的半径
R = 较大圆的半径
l = 截头锥体的斜高

圆台总表面积：
总表面积 (TSA) = pi * l(R + r) + pi(R^2 + r^2 )
其中
r = 较小圆的半径
R = 较大圆的半径
l = 截头锥体的斜高

例子：
输入：小圆的半径 = 3
        大圆的半径 = 8
        截头体的高度 = 12
        截头体的斜高 = 13
输出：
圆台体积：1218.937
圆台曲面面积：449.24738 圆台
总表面积：678.58344

输入：小圆的半径 = 7
        大圆的半径 = 10
        截头体的高度 = 4
        截头体的斜高 = 5
输出：
圆台体积：917.34436
圆台曲面面积：267.03516
圆台总表面积：735.1321

示例代码：

// Function to calculate Volume of frustum of cone
function volume(r, R, h) {
    const pi = 3.14159;
    return (1 / 3) * pi * h * (r * r + R * R + r * R);
}

// Function to calculate Curved Surface area of frustum of cone
function curvedSurfaceArea(r, R, l) {
    const pi = 3.14159;
    return pi * l * (R + r);
}

// Function to calculate Total Surface area of frustum of cone
function totalSurfaceArea(r, R, l, h) {
    const pi = 3.14159;
    return pi * l * (R + r) + pi * (r * r + R * R);
}

// Driver function
function main() {
    const smallRadius = 3;
    const bigRadius = 8;
    const slantHeight = 13;
    const height = 12;

    // Printing value of volume and surface area
    console.log("Volume Of Frustum of Cone : " + volume(smallRadius, bigRadius, height));
    console.log("Curved Surface Area Of Frustum of Cone : " + curvedSurfaceArea(smallRadius, bigRadius, slantHeight));
    console.log("Total Surface Area Of Frustum of Cone : " + totalSurfaceArea(smallRadius, bigRadius, slantHeight, height));
}

// Calling the main function
main();

输出：

圆锥台体积：1218.937
圆锥台曲面面积：449.24738
圆锥台总表面积：678.58344

如果您喜欢此文章，请收藏、点赞、评论，谢谢，祝您快乐每一天。