量子化学计算（Gausssian）图形工作站硬件方案

最新推荐文章于 2025-02-19 08:54:00 发布
转载 最新推荐文章于 2025-02-19 08:54:00 发布 · 1k 阅读 · 1 ·
CC 4.0 BY-SA版权
原文链接：https://blog.youkuaiyun.com/Su_wenfeng/article/details/79456396

本文探讨了量子化学计算中不同算法对硬件配置的要求，包括CPU、内存、硬盘和GPU，介绍了UltraLAB图形工作站针对高精度计算的优化配置，旨在帮助科研人员选择合适的硬件以提高计算效率。

（一）量子化学计算如何选择硬件配置
由于分子的类型、体系和模拟算法，以及各种应用和精度要求，都有不同的计算特点，对计算机硬件（CPU、内存、硬盘、GPU）配置要求有很大的差异 ，那么如何选择好服务器/工作站的硬件配置，提高计算速度，缩短求解时间？主要看用量子化学计算软件的算法，及做什么求解，因为算法和精度决定了计算特点和求解规模，合理的硬件配置，大大发挥机器性能，缩短求解时间。

主要量子化学软件：Gaussian，GAMESS，MOLPRO，NWChem
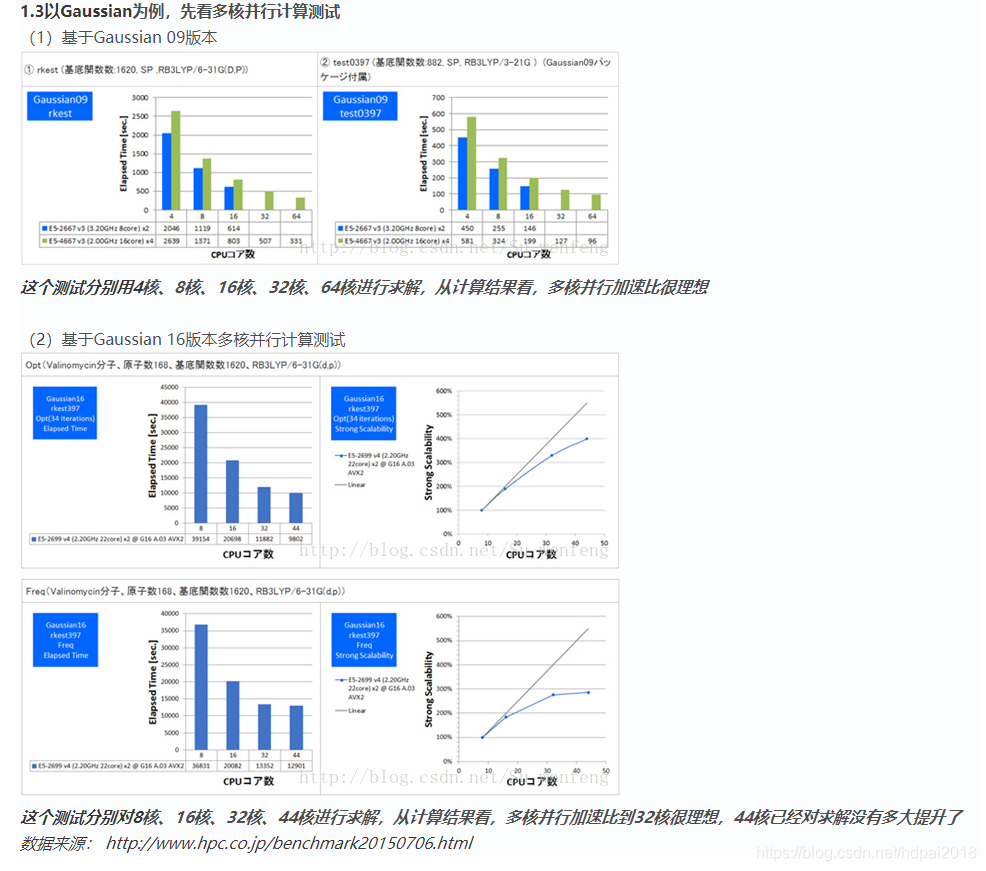
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

1.4 量子化学计算硬件配置特点
（1）不同算法的并行计算的核数加速比有所差异，不完全是线性的
（2）最新CPU架构和提升频率，对缩短求解时间非常显著
（3）精度高求解计算量大，对CPU频率和核数、内存容量、硬盘io要求均有很高要求

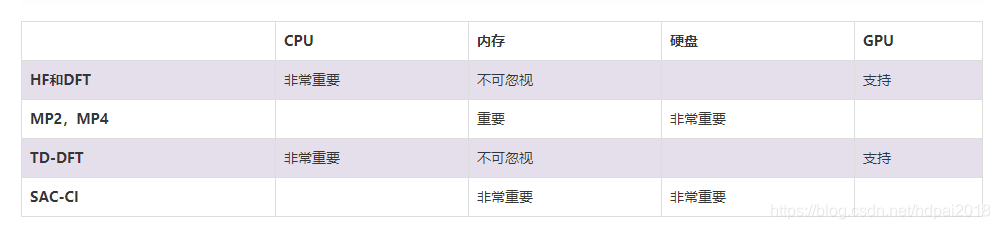
在这里插入图片描述
数据来源：http://www.hpc.co.jp/chem/c_select_hardware.html

（4）核数与内存比例为 1:4最为理想
（5）支持Tesla K40或K80 的GPU计算，显存需12GB以上，但算法有局限性，同时性价比不好
（6）组成集群的计算节点配置最好采用4核~10核超高频，效率最高

（二）基于量子化学计算，UltraLAB完美硬件配置推荐
2.1 UltraLAB图形工作站机型介绍

UltraLAB是西安坤隆计算机科技有限公司推出的定制图形工作站品牌，经过多年发展，该产品拥有傲视群雄的三大领先优势：先进计算硬件架构、完整齐全行业应用定制方案、专业硬件系统优化技术，大幅超越同类的“图形工作站”产品。以下是基于量子化学计算应用最快硬件架构产品系列：

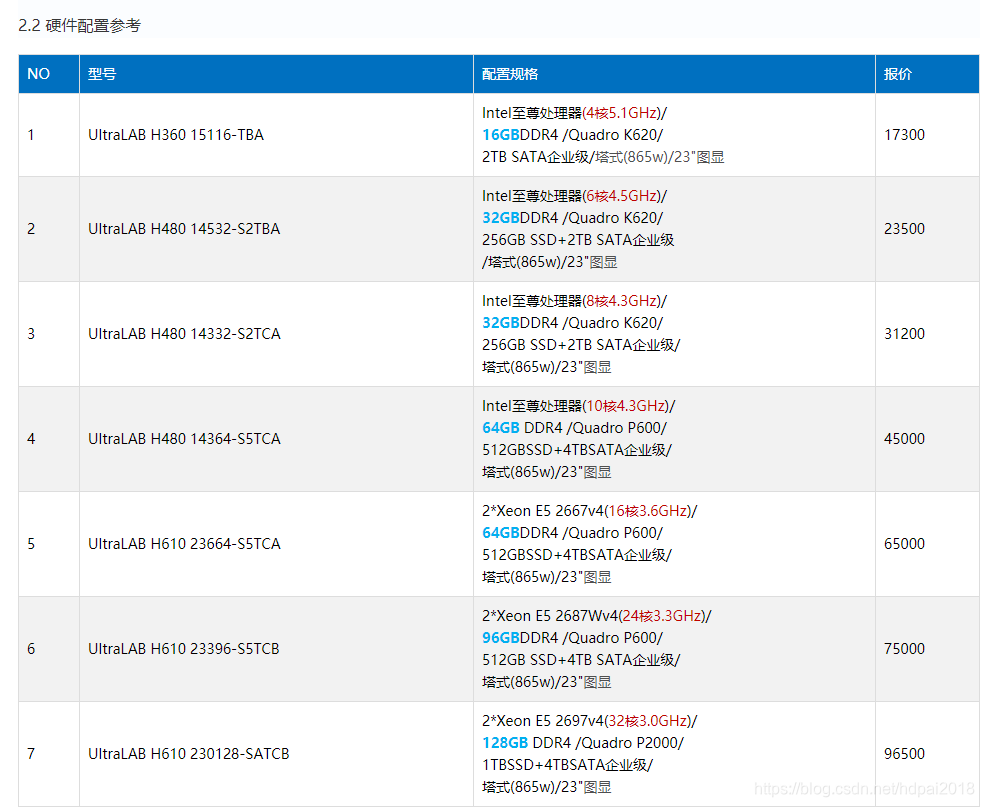
在这里插入图片描述

在这里插入图片描述

在这里插入图片描述
备注：以上价格仅供参考

上述配置其显著特点，
（1）全部采用最新intel硬件架构
（2）提供不用规模的高效完美硬件配置，满足不同算法和精度计算需求
（3）每个配置架构，CPU频率达到极致，提升性能关键指标
（4）足够多核数，并行存储高io，满足高精度计算，均衡无死角
（5）整机全部提供系统优化，大幅提升计算速度
（6）支持GPU计算扩展

————————————————
版权声明：本文为优快云博主「於無聲處聽驚雷」的原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.youkuaiyun.com/Su_wenfeng/article/details/79456396

量子化学仿真软件：Gaussian_（14）.多尺度模拟方法
kkchenjj的博客
08-30 738
多尺度模拟方法在量子化学仿真软件中扮演着至关重要的角色，尤其是在处理复杂体系时。通过结合不同的时间和空间尺度，这些方法可以提供更全面和准确的体系行为描述。在Gaussian中，可以实现QM/MM和QM/MD方法，而混合QM/MD方法则需要通过脚本实现。这些方法在酶催化反应、溶剂化效应等实际应用中展现出了巨大的潜力和价值。希望本文对您了解多尺度模拟方法及其在Gaussian中的实现有所帮助。如果您有任何问题或需要进一步的帮助，请随时联系。
量子化学计算机程序,量子化学
weixin_39946313的博客
07-19 1846
NWChem安装版本：6.5 最新版本：6.8.1License:Educational Communityc 2.0软件介绍NWChem是运行在高性能并行超级计算机和通常工作站集群上的计算化学软件，可以用在大多数计算平台上。 NWChem使用标准量子力学描述电子波函或密度，计算分子和周期性系统的特性，还可以进行经典分子动力学和自由能模拟。软件类型开源软件 Educational Communi...
MopacPro 量子化学 计算软件
05-11
MOPAC MOPAC是世界上最广泛使用的半经验量化程序 MOPAC是世界上最广泛使用的半经验量化程序，用于研究气体，溶液和固体的化学特性，包括Gibbs自由能，活化能，反应路径，偶极矩，非线性光学特性以及红外光谱，等。它还可以用做为结构-特性（或活性）定量的基础，预测生物学及其它特性，包括致癌性，蒸汽压，水溶解性，反应率等。MOPAC中获取专利的MOZYME算法可以使那些在超级计算机上需要几天或者几周的计算，在 PC机上仅需要几分钟。对于包含上千原子的体系，诸如蛋白质，聚合物，半导体和晶体，它们的电子特性计算仅仅需要几分钟或几小时。 此外，MOPAC还包含用于光谱计算的半经验分子轨道程序MOS-F模块（目前版本是5.0）。MOPAC和MOS-F本身并不包含图形用户界面，但可以和CAChe，LinMOPAC，WinMOPAC，HyperChem或CS Chem3D等图形用户界面的程序结合使用。 MOPAC早先作为免费软件发布，最高版本为MOPAC 7.0。此后成为商业软件。目前的版本是MOPAC 2006。 基本功能： 1. 计算方法有：在MOPAC中有：AM1，AM1-d，PM3，MNDO，MNDO-d，MINDO/3；在MOS-F中有：CNDO/2，CNDO/S，CNDO/S2，CNDO/S3，INDO/S。 适用原子： MINDO/3（H，B，C，N，O，F，Si，P，S，Cl）； MNDO（1977）（H，Li，Be，B，C，N，O，F，Na，Mg，Al，Si，P，S，Cl，K，Ca，Zn，Ga，Ge，As，Se，Br，Rb，Sr，Cd，In，Sn，Sb，Te，I，Cs，Ba，Hg，Tl，Pb，Bi，S，Cb）； AM1（H，Li，Be，B，C，N，O，F，Na，Mg，Al，Si，P，S，Cl，K，Ca，V，Fe，Cu，Zn，Ga，Ge，As，Se，Br，Rb，Sr，Mo，Pd，Ag，Cd，In，Sn，Sb，Te，I，Cs，Ba，Pt，Hg，Tl，Pb，Bi，Si，S，Cb）； PM3 (1985)（H，Li，Be，B，C，N，O，F，Na，Mg，Al，Si，P，S，Cl，K，Ca，Ti，Zn，Ga，Ge，As，Se，Br，Rb，Sr，Cd，In，Sn，Sb，Te，I，Cs，Ba，Hg，Tl，Pb，Bi，Cb）； PM5（H，Li，Be，B，C，N，O，F，Na，Mg，Al，Si，P，S，Cl，K，Ca，Zn，Ga，Ge，As，Se，Br，Rb，Sr，Cd，In，Sn，Sb，Te，I，Cs，Ba，Hg，Tl，Pb，Bi）； mndo_d（Na，Mg，Al，Si，P，S，Cl，Zn，Br，Cd，I，Hg）。 2. 可以进行的计算有：几何优化，过渡态结构，激发态结构，线性比例SCF计算(MOZYME方法)，反应坐标能量图，生成热（气相或溶液），简正模式振动分析，溶剂特性（气相，水，辛醇等），IR光谱，原子电荷，极化率，偶极矩，分子轨道，电子密度，梯度范数，力，能量分配，ESP原子电荷，键序，参量化分子静电势，体系间交叉结构，氨基酸片断顺序的结构分析，IRC/DRC。 3. 支持的输入文件格式：MOPAC，MOS-F，Gaussian输入文件(*.gjf)，Gaussian fchk文件(*.fch)，Cartesian文件(*.car)，PDB。 4. XMO工具可以显示分子。 MOS-F 1. 进行半经验分子轨道方法INDO/S，CNDO/S，CNDO/S2，CNDO/S3，CNDO/2等的计算。 2. 单电子激发组态相互作用(CIS)的光谱计算，支持单重激发态和三重激发态。CIS还能计算激发态的电子密度和电偶极矩。 3. 随机相位近似(RPA)的光谱计算。 4. 分子特性计算：含频极化率，静态第一超极化率，电-光泡克尔效应，产生二次谐波，光学检波，静态第二超极化率，包含克尔效应的直流电场，包含二次谐波的直流电场，产生三次谐波，简并四波混频，包含光学检波的直流电场。 5. 用Onsager模型进行SCRF计算，预测溶液中的分子特性：CIS/RPA波函的电子光谱；用CIS波函预测激发态的电子密度和电偶极矩；用CIS波函计算含频极化率，第一超极化率和第二超极化率。 6. 解析的Pariser-Parr， Nishimoto-Mataga， Nishimoto-Mataga-Weiss，Ohno，Ohno-Klopman和DasGupta-Huzinaga公式，用于求解双中心电子排斥积分。 7. 支持的坐标输入格式有Gaussian型Z矩阵和MOPAC内坐标。 8. 到WinMOPAC的输入/输出接口。 9. 对溶质，自动计算空穴半径；通过指定溶剂名称，自动设置介电常数和折射率。 10. 改善SCF收敛的DIIS方法。 11. 转动常数，惯量主轴和偶极矩的夹角。 MOPAC2002 V1.5和WinMOPAC 3.9的新功能： 1. MINDO，AM1，PM3，PM5新增加对13种过渡金属（Sc,Ti,V,Cr,Fe,Co,Ni,Cu,Zr,Mo,Pd,Ag,Pt）的支持。 2. MOS-F模块升级到6.0。可以用AM1，PM3，PM5计算电子光谱，支持更多的元素；考虑溶剂影响；计算极化率和超极化率；直接SCF方法；快速的直接四指数积分变换方法。 3. 线性标度COSMO方法，能够对大分子进行COSMO计算。 MOPAC2006 1.0新增功能： MOS-F模块：ROHF + CIS计算开壳层分子激发态，QM/MM-CIS/RPA计算生物大分子的激发态，INDO/S新增对Li, F, Mg, Si, P, S, Zn的支持，LAPACK提高了矩阵对角化计算的速度。 MOPAC模块：单点、几何优化、振动频率和COSMO实现并行，周期边界条件。 操作平台:Unix/Linux/Windows Mopac 2002 (通用半经验量子力学程序) 【URL】 http://www.cachesoftware.com/mopac/index.shtml 【作者】 CAChe Group, Fujitsu 【用途】 MOPAC is a general-purpose semiempirical quantum mechanics package for the study of chemical properties and reactions in gas, solution or solid-state. MOPAC directly predicts numerous chemical and physical properties such as Gibbs free energies, activation energies, reaction paths, dipole moments, non-linear optical properties and infrared spectra. It is also used as the basis of quantitative structure-property (or activity) relationships (QSAR), to predict a wide variety of biological and other properties such as carcinogenicity, vapor pressure, water solubility, and reaction rates. Macromolecules: very fast, patented, linear-scaling MOZYME optimizes proteins and DNA Materials: d-orbitals, crystals, geometry in electric fields, NLO, 2D/3D periodic boundaries Polymers: band structures, phonon spectra, Young's modulus, tensile strength Dyes: UV spectra prediction, intersystem crossing, excited states in solution Synthesis: thermodynamics, kinetics, transition-states, reaction paths, solvation, catalysis MOPAC includes the semiempirical Hamiltonians MNDO, MINDO/3, AM1, PM3, MNDO-d, and PM5. These methods have been calibrated using experimental data for thermodynamic properties such as heats of formation. AM1-d parameters are available for the following metals: Ti, V, Fe, Cu, Mo, Pd, Ag and Pt.
量子化学计算和最新分子动力学模拟计算
hdpckj的博客
11-07 2740
课程通知：(此通知长期有效！) Gaussian量化计算 12月13-15日 地点北京 Gromacs分子动力学 12月7-9日 地点上海 Lammps分子动力学 12月7-9日 地点北京 此次为答谢新老客户。精心准备量子化学Gaussian计算，全新分子动力学Gromacs和Lammps课程。全部课程都调整为三天，内容上从进阶到课题应用，所有想进阶学习或者解决问题的朋友都可以来共同学习下。 【学...
量化计算需要的计算机配置,大家好 请教做化学计算的电脑配置 - 量子化学 - 小木虫 - 学术 科研 互动社区...
weixin_42134117的博客
07-08 2226
谢谢大家指点 我的一个同学说HP有一款入门级工作站配置如下：CPU：Intel Xeon E3-1225v2 3.2 8MB 4C 77W GT2 CPU ，3.2GHz，缓存 8M， CPU个数 1 个主板：扩展槽 1个PCIe Gen3 x16、1个PCIe Gen2 x4/x16、1个PCIe Gen2 x1、1个PCI(所有插槽均为半高)芯片组 英特尔? C216 芯片组，图形卡 ...
Gaussian09 + Caussian View +海量资源
04-12
Gaussian09是一款广泛应用于化学、物理、生物等多个领域的高级量子化学计算程序，而GaussView则是一个友好的图形用户界面，使得用户能更直观地输入分子结构和控制计算参数。 在资源包中，首先我们看到的是...
diff_gaussian_rasterization 安装部署踩坑
jacke121的专栏
02-19 1778
diff_gaussian_rasterization 安装部署踩坑
Linear Quadratic Gausssian Control Design with Loop Transfer Recovery
04-30
### Linear Quadratic Gaussian (LQG) Control Design with Loop Transfer Recovery (LTR) #### 线性二次高斯（LQG）控制设计简介 线性二次高斯（LQG）控制设计是一种在控制工程领域广泛应用的方法，它结合了线性...
量子化学计算
09-06
量子化学计算是物理化学工作者研究第一性原理和化学结构必备之良器。
Gaussian_09W量子化学软件操作与应用指南
weixin_30789053的博客
12-04 3717
本文还有配套的精品资源，点击获取 简介：Gaussian系列软件是量子化学领域广泛使用的计算工具，具有模拟分子电子结构和化学性质的能力。Gaussian 09W版本特别增加了图形用户界面，简化了操作流程。用户可以使用该软件进行几何优化、频率分析、热力学性质计算等任务，以支持化学反应路径分析、电子性质计算和光谱预测。本软件指南将引导用户掌握Gaussian 09W的使用方法，...
gausssian sampling
lcmssd
03-10 705
RT
高性能服务器理论与计算化学,计算化学集群服务器简明使用指引-VLCC.PDF
weixin_42472941的博客
07-30 825
计算化学集群服务器简明使用指引-VLCC计算化学集群服务器简明使用指南v1.10 (2009-6-17)一、系统环境1)硬件环境：头结点一个，机器名 /console/node00 ，双路四核IntelXeon E5320 处理器，1.86G 主频，2*4M 缓存，4G 内存，6 块 400G SATA 硬盘，Raid5 。计算结点八个，机器名 node01-node08 双路双核 AMD Opt...
适用于 Gaussian 计算的科研服务器配置精析
finehoo_andy的博客
12-23 1472
在某些特定应用场景下，ARM 架构的服务器能够提供更经济的能耗比，这对于需要长时间运行的 Gaussian 计算来说是一个重要的考量因素。由于 Gaussian 计算涉及大量的临时数据存储和快速读取操作，如分子构型数据、计算矩阵等，因此足够的内存容量是确保计算顺利进行的必要条件。例如，在模拟生物大分子在溶液中的运动时，GPU 能够快速计算分子间的力场和构象更新，从而显著提高计算效率。在 Gaussian 计算中，存储系统的性能直接影响到计算任务的启动速度、中间结果的保存以及最终结果的存储效率。
gaussian软件linux版本,Gaussian 09的版本与平台。
weixin_34837898的博客
04-30 3507
Gaussian09的版本与平台。(2014-07-13 10:54:31)标签：gaussian量化计算Gaussian软件目前最新版本为Gaussian 09 D.01。 其中09是大版本号，D.01是小版本号。比如，从Gaussian09 C.03升级到Gaussian 09 D.01就要买Minor Reversion，也就是小版本升级。Gaussian的授权分单机版、Site lice...
高斯滤波（Gaussian filter）
热门推荐
码灵薯的博客
08-12 1万+
高斯滤波是一种线性平滑滤波，低通滤波器，可以去除高斯噪声。具体操作是：利用二维高斯分布函数，生成高斯模板，然后用模板去扫描图像中的每一个像素，用模板确定的领域内像素的加权平均值作为新图像中模板中心位置的像素值。 常用的二维高斯分布函数 G(x,y)=e−x22∗σ21−y22∗σ22G(x,y)=e−x22∗σ12−y22∗σ22 G(x,y) = e^{ -\frac{x^2}{2*\si...
Ubuntu20.04+Quadro RTX 5000，3D gaussian环境配置
weixin_44368569的博客
09-10 9090
2020年，NeRF的出现之际引起了轩然大波，出现了大量相关工作。3D gaussian算是新视角生成领域目前的SOTA，可以进行实时的渲染；最大训练速度上可以与Instant相当，且质量差不多；增加迭代次数后，可以显著提高重建质量，在训练时间51min的情况下，重建效果可以稍微超过Mip-NeRF（48h）。这种好东西谁不想学习下呢，所以我们先进行第一步：配置3D gaussian环境。我当前的环境为ubuntu 20.04+Quadro RTX 5000。
clear all; clc; % Specify input parameters mshape = 3; % pulse shape mshap=0 for sech, mshape>0 for super-Gausssian chirp0 = 0; % input pulse chirp (default value) beta2 = -1; % dispersion of fober %%%%%%%%%%% set simulation parameters nt = 1024; Tmax = 32; % FFT points and window size dtau = (2*Tmax)/nt; % step size in tau %%%%%%%%% tau and omega arrays tau = (-nt/2:nt/2-1)*dtau; % temporal grid omega = (pi/Tmax)*[(0:nt/2-1) (-nt/2:-1)]; % frequency grid %%%%%%%%%%%%%%%%%%%%%%%%%%%% output parameters z1=2;% z/Ld=2 z2=4;% z/Ld=4 %%%%%%%%% Input Field profile if mshape==0 uu = sech (tau).*exp(-0.5i*chirp0*tau.^2); % soliton else % super-Gaussian uu = exp(-0.5*(1+i*chirp0).*tau.^(2*mshape)); end %%%%%%%%% Plot input pulse shape and spectrum figure(1); plot(tau, abs (uu).^2, '-.'); hold on; axis([-10 10 0 1.1]); xlabel('时间，T/TO'); ylabel('归一化强度'); %%% Plot output pulse at z=2*Ld uzw1=fft (uu).*exp(0.5i*beta2*omega.^2*z1); % 计算z=0处输入信号的FFT，然后乘以指数EXP[],得z1处的信号的FFT uz1=ifft(uzw1);% 得z1处的时域信号 plot(tau, abs (uz1).^2, 'r'); % 绘图，横轴为T/T0，纵轴为幅度的平方 %%% Plot output pulse at z=4*Ld uzw2=fft (uu).*exp(0.5i*beta2*omega.^2*z2); % uz2=ifft(uzw2); plot(tau, abs (uz2).^2, 'g'); legend('z/LD=0','z/LD=2','z/LD=4') ;% 设置图例 %%%%%%%%%%%% 补充频率啁啾、展宽因子与归一化时间的关系图 if mshape>=1 % plot 高斯脉冲的频率啁啾与归一化时间的关系图 figure(2) domegaT0=sign(beta2)*0.*tau/(1+0^2); plot(tau, domegaT0, '-.'); hold on; axis([-10 10 -6 6]); xlabel('时间，T/TO'); ylabel('频率啁啾，domega*T0'); %%% Plot output pulse at z=2*Ld domegaT=sign(beta2)*z1.*tau/(1+z1^2); plot(tau, domegaT, 'r'); %%% Plot output pulse at z=4*Ld domegaT=sign(beta2)*z2.*tau/(1+z2^2); plot(tau, domegaT, 'g'); legend('z/LD=0','z/LD=2','z/LD=4') ;% 设置图例 end
最新发布
10-14
<think>我们被要求理解和优化一段MATLAB代码，该代码涉及脉冲形状、频谱计算及绘图，包含输入参数设置、时域和频域信号处理。根据引用内容，代码可能涉及雷达信号或心电信号的处理，但根据用户描述，我们关注的是脉冲形状（可能是LFM脉冲信号）以及频谱分析。 由于用户没有提供具体的代码，但根据引用[1]描述，代码可能包含以下步骤： 1. 定义信号的基本参数（采样频率、脉冲宽度、信号带宽等）。 2. 生成一个LFM（线性调频）脉冲信号。 3. 对信号进行时域和频域的分析与绘制。 因此，我们可以假设一个典型的LFM信号生成和频谱分析的MATLAB代码框架，并针对这样的框架进行优化和解释。 典型的LFM信号生成代码可能如下（未优化）： ```matlab % 参数设置 fs = 1e6; % 采样频率 (Hz) T = 100e-6; % 脉冲宽度 (s) B = 100e3; % 信号带宽 (Hz) f0 = 0; % 起始频率 (Hz)，通常对于基带信号从0开始 N = round(fs * T); % 采样点数 % 生成时间向量 t = linspace(-T/2, T/2, N); % 生成LFM信号（复信号形式） s = exp(1i * pi * (B/T) * t.^2); % 时域绘图 figure; plot(t, real(s)); xlabel('时间 (s)'); ylabel('幅度'); title('LFM信号（实部）时域波形'); % 频域分析 NFFT = 2^nextpow2(N); % FFT点数 S = fftshift(fft(s, NFFT)); f = linspace(-fs/2, fs/2, NFFT); % 频域绘图（幅度谱） figure; plot(f, abs(S)); xlabel('频率 (Hz)'); ylabel('幅度'); title('LFM信号幅度谱'); ``` 优化点： 1. 代码效率：在生成LFM信号时，使用向量化操作已经高效。但如果N很大，可以考虑使用gpuArray加速（如果支持GPU）或使用单精度减少内存（如果精度允许）。 2. 参数设置：可以增加灵活性，例如允许用户输入参数，或者通过函数封装。 3. 绘图优化：对于频谱，有时使用dB单位更合适，可以增加20*log10(abs(S))的绘图，并注意避免零分贝以下的噪声被截断（可以设置动态范围）。 4. 代码健壮性：检查采样点数N是否为整数，使用round确保整数。 5. 频谱泄漏：在FFT前加窗（如汉明窗）可以减少频谱泄漏，但需要根据应用决定（LFM信号本身频谱较宽，通常矩形窗即可，因为脉冲内幅度恒定）。 6. 内存使用：如果数据量非常大，可以考虑使用分段处理或使用fft函数的单精度版本（如fft(single(s))）。 下面给出优化后的代码示例，并添加注释解释： ```matlab % 参数设置 fs = 1e6; % 采样频率 (Hz) T = 100e-6; % 脉冲宽度 (s) B = 100e3; % 信号带宽 (Hz) f0 = 0; % 起始频率 (Hz)，这里假设是基带信号 N = round(fs * T); % 采样点数，确保整数 % 时间向量：采用列向量，有利于内存连续访问（MATLAB中列向量效率更高） t = linspace(-T/2, T/2, N).'; % 生成LFM信号（复信号形式） % 注意：线性调频信号的相位为 pi*(B/T)*t^2 s = exp(1i * pi * (B/T) * t.^2); % 时域绘图（只显示实部） figure; plot(t*1e6, real(s)); % 时间转换为微秒 xlabel('时间 (\mus)'); ylabel('幅度'); title('LFM信号时域波形（实部）'); grid on; % 频域分析 % 使用nextpow2确定FFT点数，也可以用N，但补零到2的幂次可以加速FFT NFFT = 2^nextpow2(N); % 进行FFT，并移位 S = fftshift(fft(s, NFFT)); % 频率向量 f = linspace(-fs/2, fs/2, NFFT).'; % 频域绘图（幅度谱）使用dB单位 figure; plot(f/1e3, 20*log10(abs(S)/max(abs(S)))); % 频率转换为kHz，归一化并取对数 xlabel('频率 (kHz)'); ylabel('幅度 (dB)'); title('LFM信号归一化幅度谱'); grid on; ylim([-100, 0]); % 设置动态范围为-100dB到0dB，便于观察 % 可选：绘制相位谱（如果需要） figure; plot(f/1e3, angle(S)); % 注意相位在幅度很小的地方没有意义 xlabel('频率 (kHz)'); ylabel('相位 (rad)'); title('LFM信号相位谱'); grid on; ``` 优化说明： 1. 时间向量采用列向量（.'转置，非共轭转置），有利于提高内存访问效率。 2. 在绘图时，将时间转换为微秒（us），频率转换为千赫兹（kHz），使得坐标轴刻度更易读。 3. 频谱使用归一化的dB单位，并设置动态范围（-100dB到0dB），这样可以看到主瓣和旁瓣的相对幅度。 4. 增加了网格线（grid on）使图表更易读。 注意：以上代码假设生成的是基带LFM信号（中心频率为0）。如果需要带通信号（例如中心频率fc），则信号生成公式为： s = exp(1i * 2*pi*fc*t) .* exp(1i * pi*(B/T)*t.^2); 如果用户提供的代码有特定问题，请提供具体代码以便进一步优化。如果没有，上述优化后的代码可以作为参考。 另外，根据引用[3]和[4]，用户可能是在一个GUI系统中进行信号处理。如果代码需要嵌入GUI，可以考虑将上述代码封装为函数，并在GUI回调函数中调用。 如果用户代码中存在错误，常见错误可能包括： - 时间向量构建错误（对称区间不正确）。 - 调频斜率符号错误（正负号影响向上或向下调频）。 - FFT变换后忘记移位（fftshift）。 - 频率向量构建错误（范围应该是-fs/2到fs/2，点数与FFT点数匹配）。 请用户提供具体代码以便更准确地查找错误和优化。 </think>### MATLAB信号处理代码优化与理解 针对脉冲信号处理、频谱计算及绘图的MATLAB代码优化，以下是关键优化点和实现原理分析： #### 1. **参数设置优化** ```matlab % 原始代码可能存在的问题：硬编码参数不便修改 fs = 1e6; % 采样频率 (Hz) pulseWidth = 100e-6; % 脉冲宽度 (s) bandwidth = 100e3; % 信号带宽 (Hz) % 优化方案：参数结构体封装 params = struct(... 'fs', 1e6, ... % 采样频率 'pulseWidth', 100e-6, ... 'bandwidth', 100e3, ... 'f0', 0 ... % 起始频率 ); ``` **优化理由**：结构体封装提高代码可读性和参数重用性[^1] #### 2. **LFM信号生成优化** ```matlab % 原始实现可能存在效率问题（采样点数计算） t = linspace(-params.pulseWidth/2, params.pulseWidth/2, ... round(params.fs * params.pulseWidth)); % 优化后向量化计算 nSamples = round(params.fs * params.pulseWidth); t = linspace(-params.pulseWidth/2, params.pulseWidth/2, nSamples).'; lfmSignal = exp(1i * pi * (params.bandwidth/params.pulseWidth) * t.^2); ``` **原理说明**：[^1] - `t.^2`实现二次相位调制（线性调频核心） - 复指数形式`exp(1i*phi)`保留完整相位信息 - 列向量(`.'`)提升内存访问效率 #### 3. **频谱计算优化** ```matlab % 原始FFT可能未优化点数 nfft = 2^nextpow2(length(lfmSignal)); % 优化为2的幂次 spectrum = fftshift(fft(lfmSignal, nfft)); freqAxis = (-params.fs/2 : params.fs/nfft : params.fs/2 - params.fs/nfft).'; % 幅度谱计算避免重复运算 powerSpectrum = abs(spectrum).^2 / nfft; % 功率谱密度 ``` **优化点**：[^1][^2] - `nextpow2`加速FFT计算 - 归一化处理保证能量守恒 - 频率轴精确映射 #### 4. **绘图优化技巧** ```matlab % 时频域对比绘图 figure('Position', [100, 100, 800, 600]) % 时域（子图1） subplot(2,1,1) plot(t*1e6, real(lfmSignal)) title('LFM脉冲时域波形') xlabel('时间(\mus)'), ylabel('幅度') grid on % 频域（子图2） subplot(2,1,2) plot(freqAxis/1e3, 10*log10(powerSpectrum)) title('功率谱密度') xlabel('频率(kHz)'), ylabel('功率(dBW)') xlim([-params.bandwidth*1.5/1e3, params.bandwidth*1.5/1e3]) ``` **优化点**：[^3] - 图形窗口尺寸预设 - 物理单位转换（μs/kHz） - 动态范围聚焦信号带宽 - dB刻度增强可视化 ### 常见错误修复 1. **频率轴错位**：确保`fftshift`与频率轴同步 2. **能量泄露**：增加窗函数补偿（如Hamming窗） ```matlab window = hamming(length(lfmSignal)); spectrum = fftshift(fft(lfmSignal .* window, nfft)); ``` 3. **复数信号处理**：雷达信号需保持复信号处理 ### 性能优化策略 1. **内存预分配**： ```matlab t = zeros(nSamples, 1); % 预分配内存 ``` 2. **GPU加速**（需支持）： ```matlab if gpuDeviceCount > 0 lfmSignal = gpuArray(lfmSignal); end ``` 3. **并行计算**：对多脉冲处理使用`parfor` ### 应用扩展建议 1. **时频分析**：增加短时傅里叶变换(STFT) ```matlab spectrogram(lfmSignal, 128, 120, 256, params.fs, 'yaxis') ``` 2. **脉冲压缩**：添加匹配滤波器实现 ```matlab matchedFilter = conj(fliplr(lfmSignal)); compressed = conv(lfmSignal, matchedFilter); ```
评论
成就一亿技术人!
拼手气红包6.0元
还能输入1000个字符
 
红包 添加红包
表情包 插入表情
表情包 代码片
 条评论被折叠 查看
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值