Games101笔记 P1 transformation

最近刚学完了games101课程，做了一些课程笔记，只挑着比较重要的点记的，我理解的可能不是很深，有些地方可能有错误，欢迎指正，这是第一部分的内容，对应games101中P3-P4的内容

1.M（模型）V（视图）P（投影）变换， 作用：从三维世界到二维世界（本质上就是人在拍照）

M变换，原理就是看x’=ax+by y’=cx+dy，只要能找到他们的关系，就能够写出变换矩阵

2.变换矩阵的理解：
矩阵在左，向量（坐标）在右，一般地，矩阵都是方阵（n x n），向量都是列向量（n x 1），那么结果就是一个（n x 1）的向量，第一行为x‘（由变换矩阵乘向量得到）， 第二行为y’ ，第三行为z‘

3.旋转矩阵：（能够自己推导）
R = cos -sin
sin cos

4.齐次坐标（先进行线性变换，在进行平移）
引入齐次坐标是为了统一平移变换，仿射变换：线性变换（缩放，旋转，切变） +平移
原理是增加一个维度，令点为1 向量为0

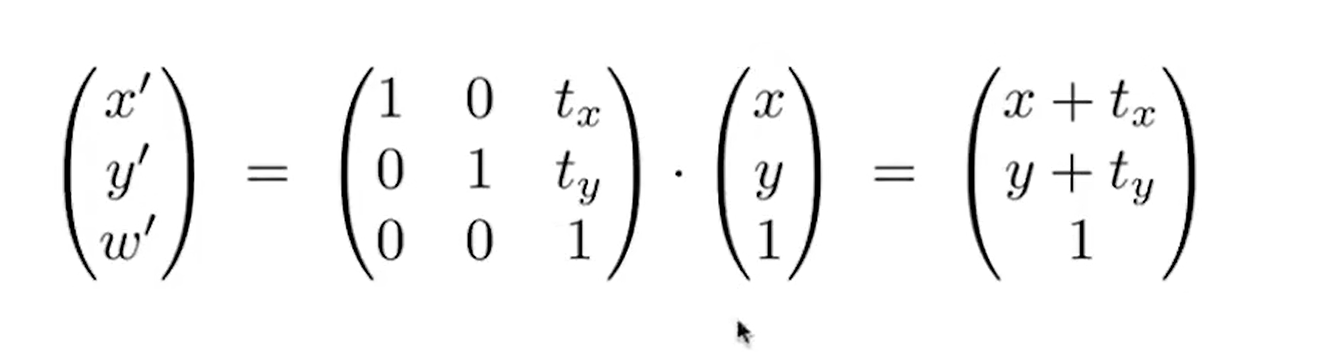
（x，y，1）表示一个点，变换矩阵最后（0，0，1）是精髓，即第三行与（x，y）这个点无关，与（x，y，1）相乘后得到的仍为1，即表示一个点，tx ，ty表示的是平移距离，与（x，y，1）的1相乘保持不变

5.逆变换
即乘逆矩阵

6.变换顺序
若有多个矩阵相乘，从右向左算，即向量先与最右边的矩阵做乘法，结果再与下一个矩阵相乘
矩阵存在结合律：可以先将所有的变换矩阵的结果求出，最后再乘向量

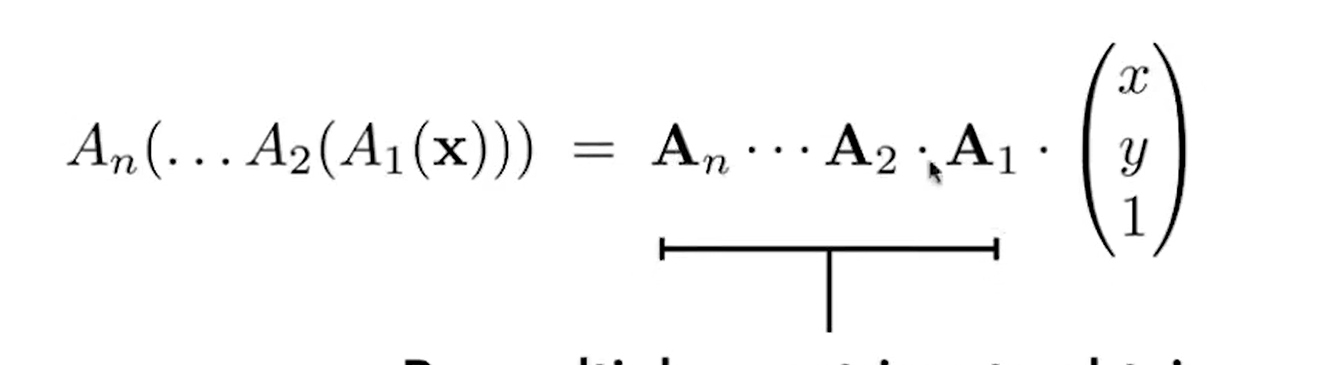
7.三维矩阵
与二维矩阵的性质相同

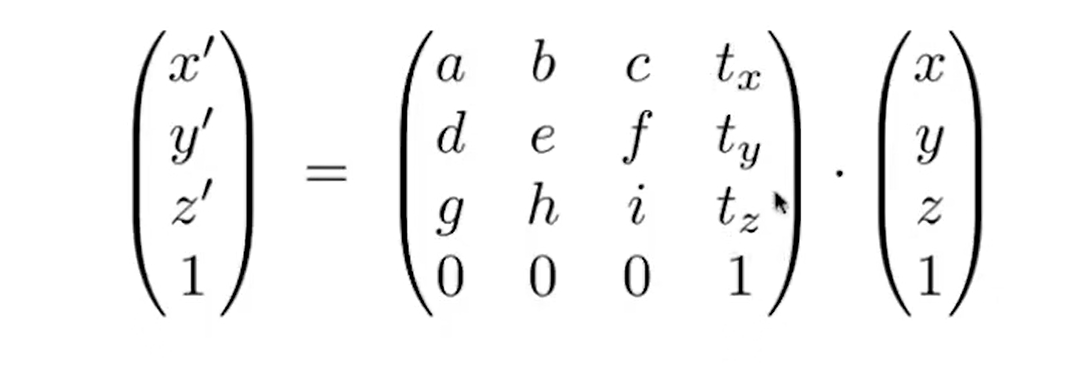
8.旋转矩阵的重要性质
旋转矩阵一定是正交矩阵，即逆等于转置 R-1=RT

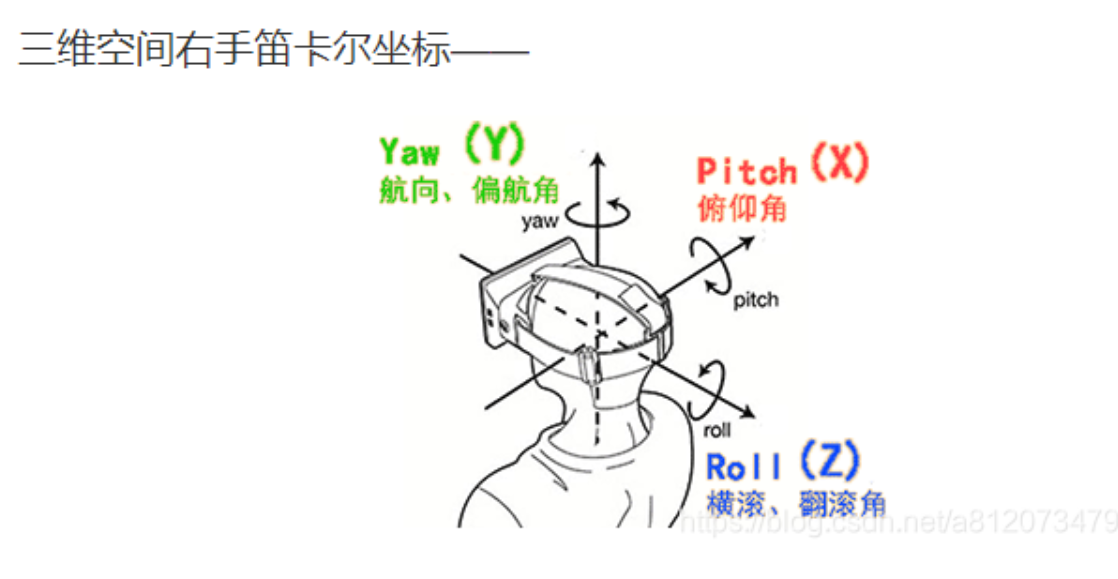
9.理解三维旋转矩阵

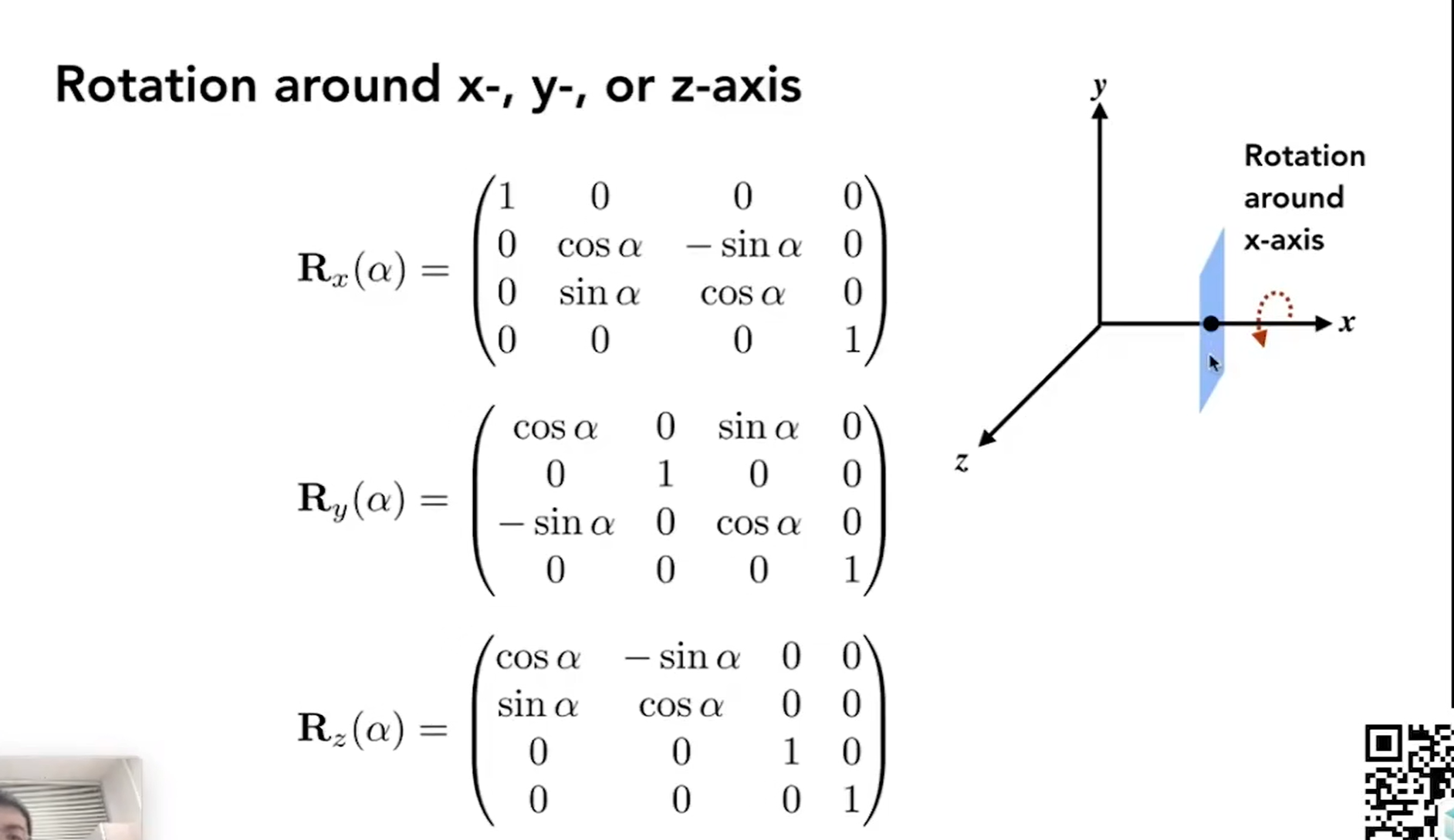
由上图可得，假设绕X轴，旋转，则x坐标不变，即x‘=x，所以第一行为（1，0，0，0），而y，z的坐标发生变化，填入二维的旋转矩阵坐标即可（因为这里相当于投影了X轴，仅在yoz平面内做旋转），而且y’ z‘的坐标与x的坐标无关，即y’ = 0x+… z‘=0x+…
重点：由于绕y轴旋转时，所建立的平面为zox面（+y轴由z X x 所得到），但是我们所需要的是xoz面（x X z 所得的是-y），所以这里要进行一个转置，转变为xoz面，相当于做逆变换

10.V（视图变换）
定义三个向量

约定：相机总是看向-Z轴，向上方向为+Y轴，在原点，e指向+X轴
从这里可以得出一个结论：当我们移动相机时，模型也跟着相机做相对运动，当相机移动到约定位置后，拍出的照片不会发生变化（本质上视图变换也是在做模型变换）
如何将摄像机调至原点？
思路：我们可以先将g向量旋转到-Z轴上，然后将e向量旋转到+X轴上，然后将t向量旋转到+Y轴上
最后将相机平移到原点上即可。

我们这里先定义几个量：
eye，相机位置，这是一个点
target，相机看向的方向，这也是一个点
up，相机的向上方向，这是一个向量
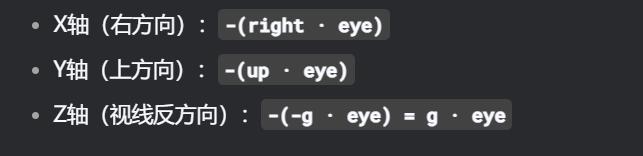
g = target-eye
t = up
right = g X t

-1 如何进行相机的平移
点乘=投影。
求eye（相机位置）在X,Y,Z轴上的投影即可，然后做反方向的平移

-2 如何旋转轴

做法：我们知道如果将某一个轴旋转到坐标轴是很困难的，所以这里我们可以先求旋转的逆矩阵，也就是从坐标轴旋转到某一个轴，然后在对这个逆矩阵求逆，我们就得到了旋转矩阵，而旋转矩阵是正交矩阵，矩阵的转置等于逆，所以我们直接求转置即可。

简单说一下为什么是上面这个矩阵
我们假设要将x轴旋转到gxt方向上，x轴是（1，0，0，0），那么这个轴去乘上面的这个矩阵，得到的结果就是（xgXt，ygXt，zgXt，0），这就旋转到了gXt轴上，同理，其他的轴也可以这样解释。

修正上方向是为了确保正交
上述代码也表示了如何构建坐标系
right=g叉乘t，就表明+X，可由g与t的叉乘得出，在右手坐标系中，+X由+Y叉乘+Z得到，而g表示的是-Z方向，所以-Z叉乘+Y可得到正确的结果+X

11.P（投影变换）
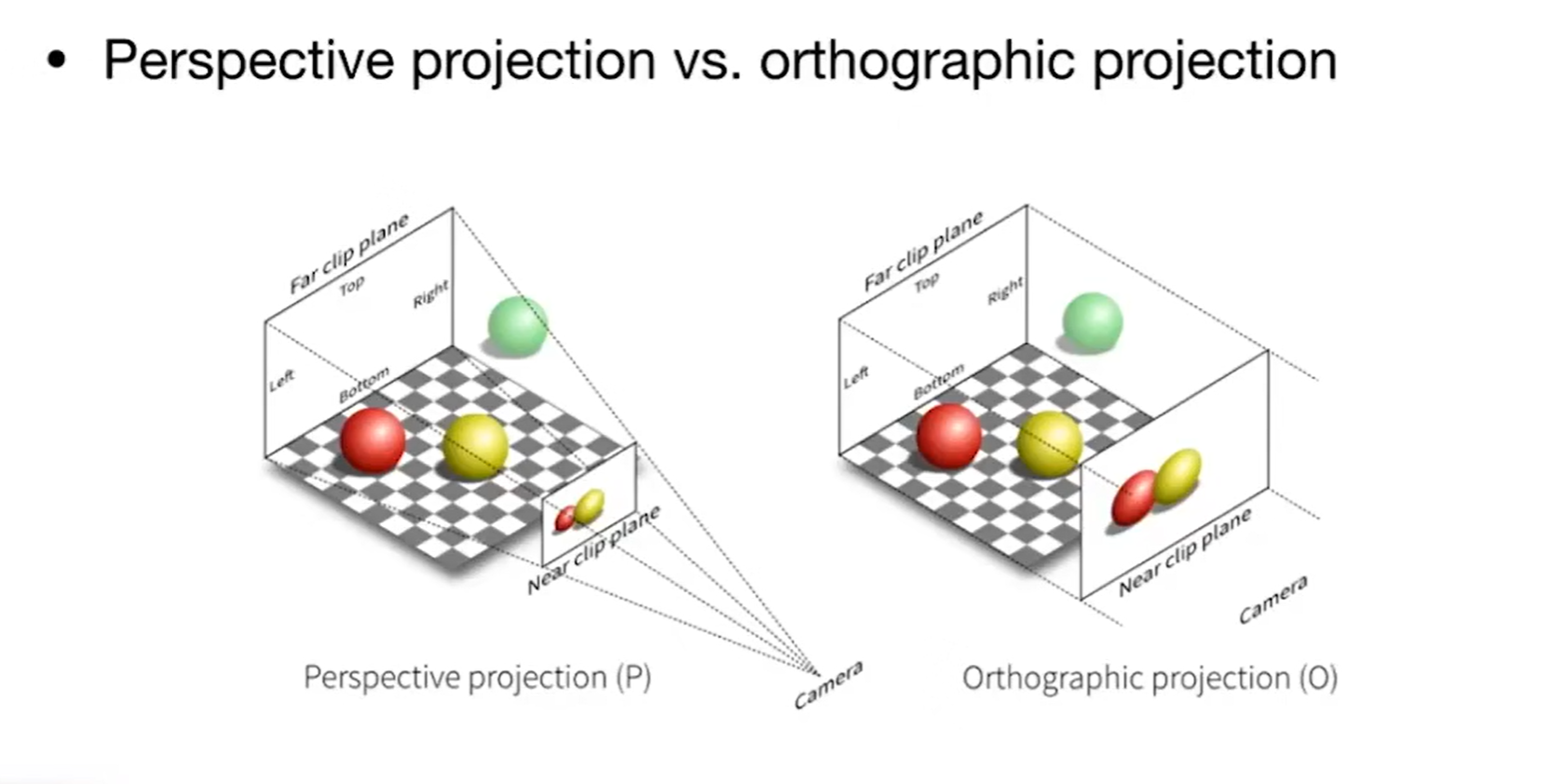
透视投影：具有进大远小效果，成像区为锥形
正交投影：不具有进大远小效果，成像区为矩形

如何完成正交投影？
（1）这种方法并没有在图形学中有着广泛的应用，算是一种比较好理解正交投影的方式
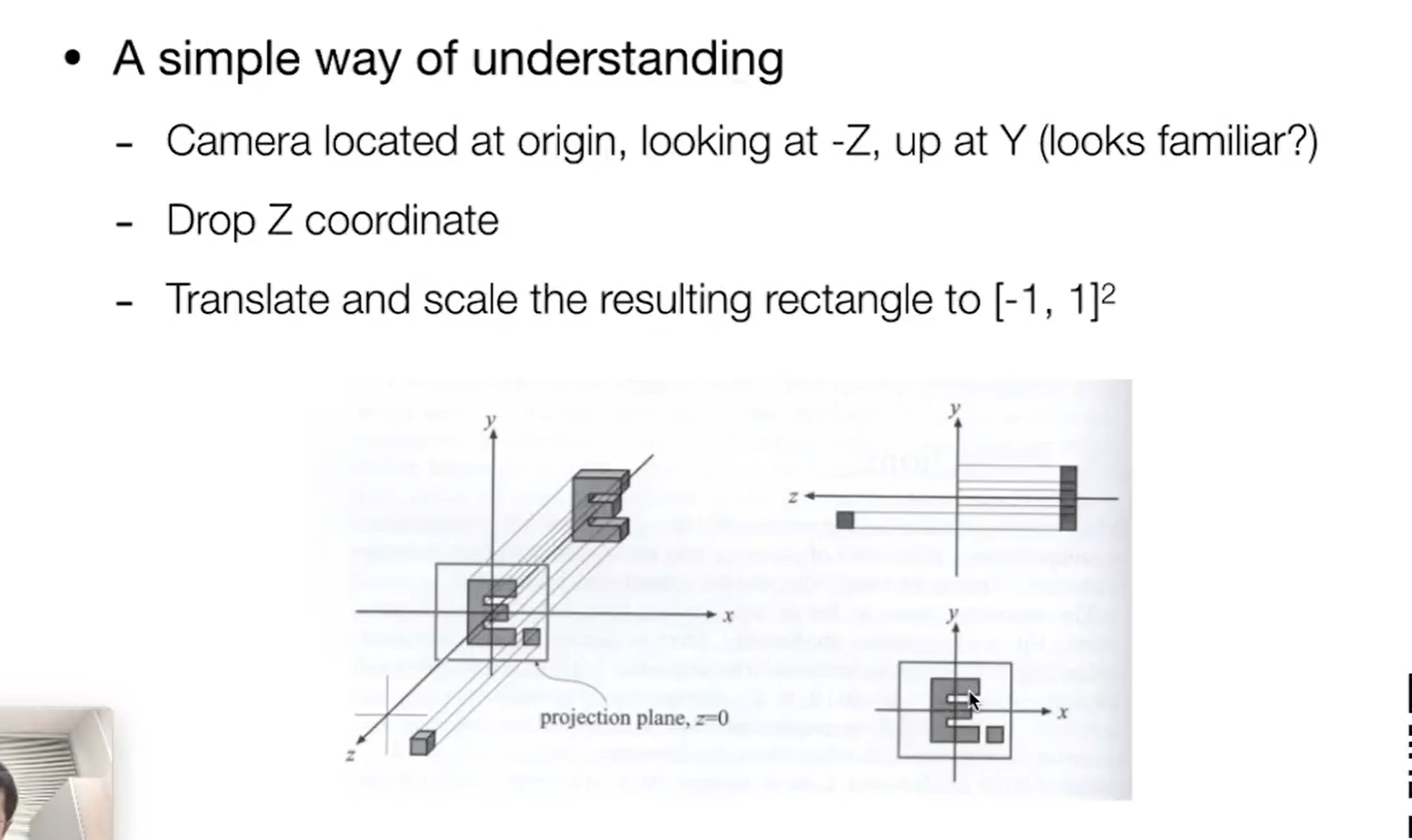
1.摆摄像机（V）
2.舍弃Z轴，只留X,Y轴
3.将摄像机成像区的大小缩放为标准型（边长为2的正方形，具体表现为 [-1 1]的正方形），模型会被拉伸，后续还会做视口变换

（2）更加一般的做法

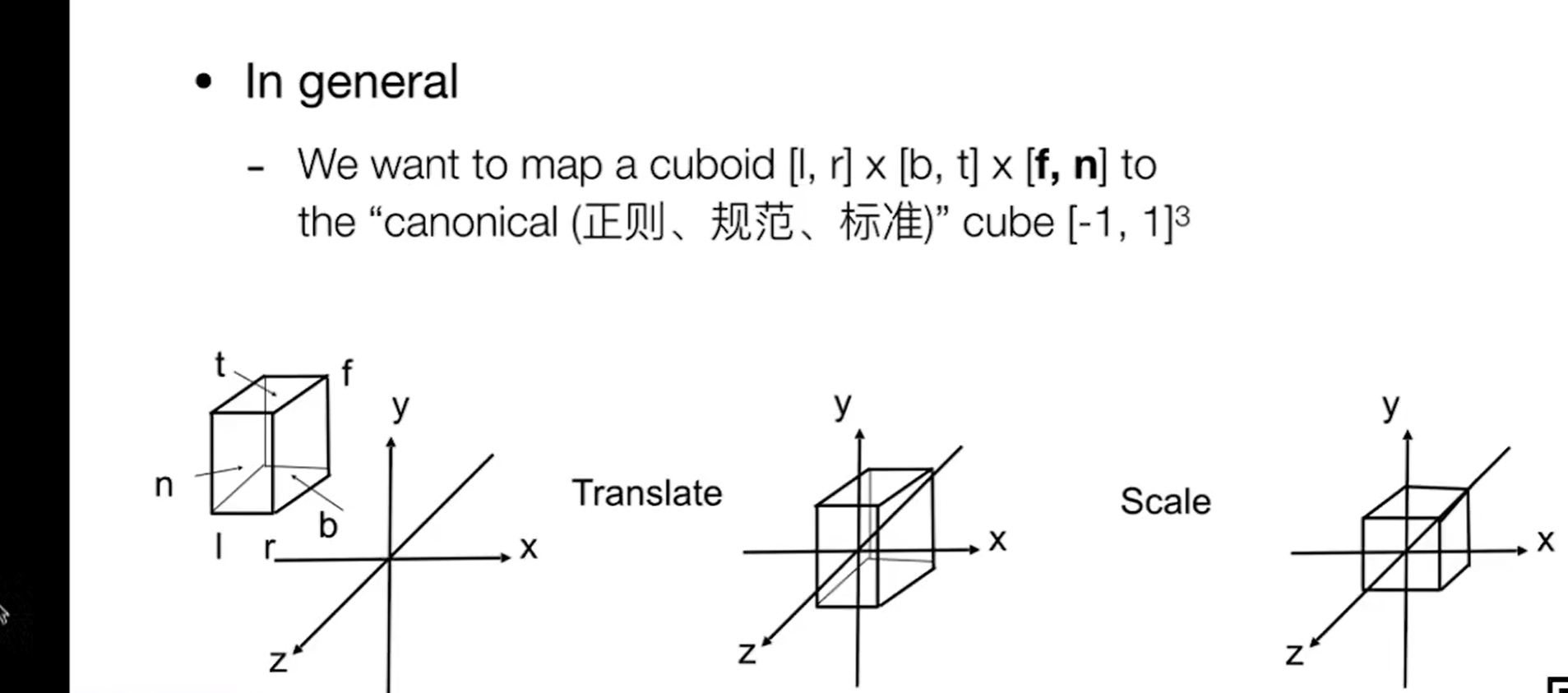
定义：我们定义了一个长方体，在Z轴上（n，f）来表示远近，在X轴上（l，r）来表示左右，在Y轴上（t，b）来表示上下，由此，我们定义了一个长方体
这里f<n 原因是向-Z轴上看

解释：
我们将这个长方体先通过平移变换，将长方体移动到原点（本质上是MV变换），然后进行缩放为[-1 1 ]的标准立方体（在这个范围之外的模型都将被裁剪），然后进行投影，即舍弃掉Z轴
这里注意一下，虽然相机在原点，但是成像区域是这个立方体。

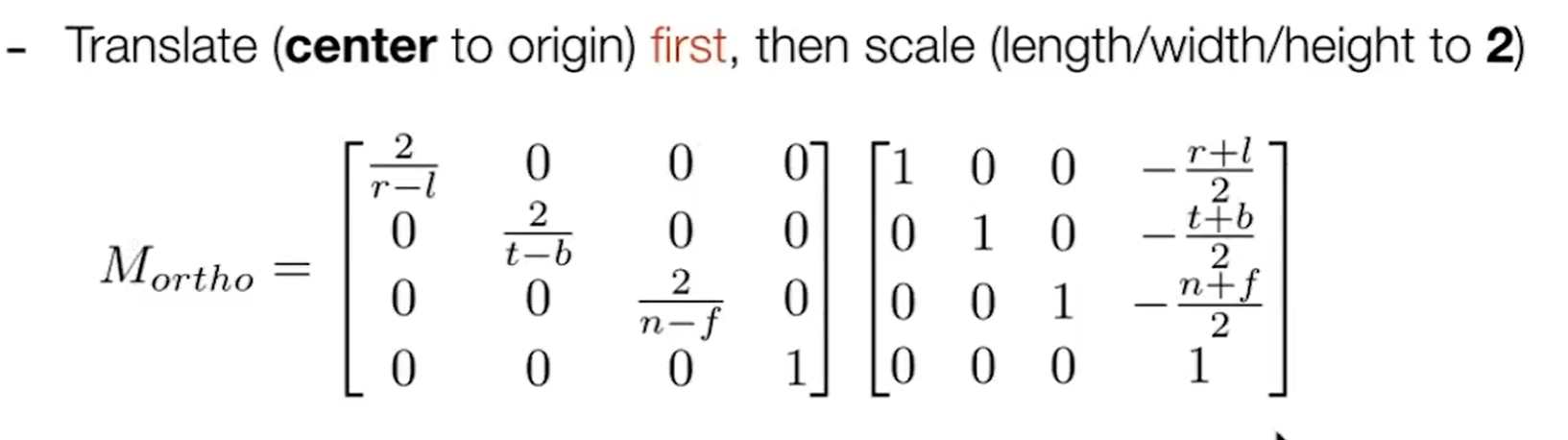
最终的正交投影矩阵：
先平移在缩放，所以这两个矩阵无法合成为一个

透视投影：
如何做透视投影？
本质就是将锥形成像区转变为矩形成像区，然后进行正交投影
锥形成像区转变为矩形成像区的推导是及其重要的。

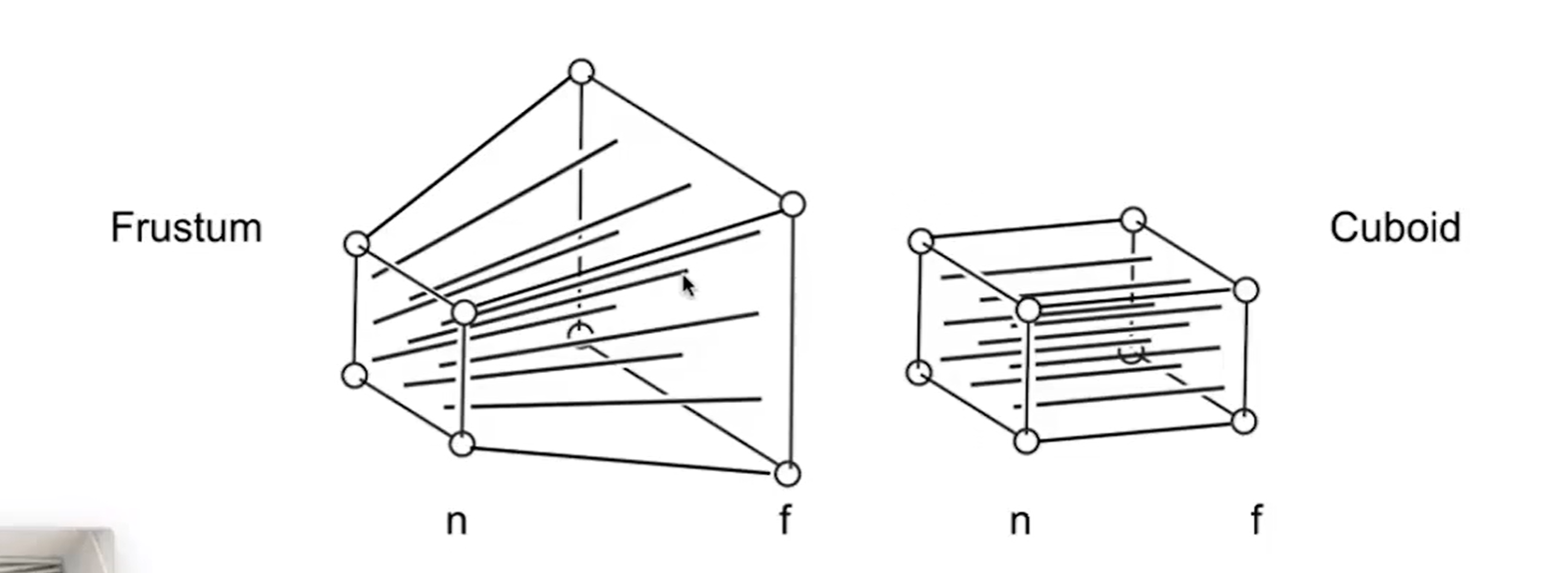
规定：近平面的每个点都不变，远平面上所有点的Z值不变，且远平面中心点不变
推导：

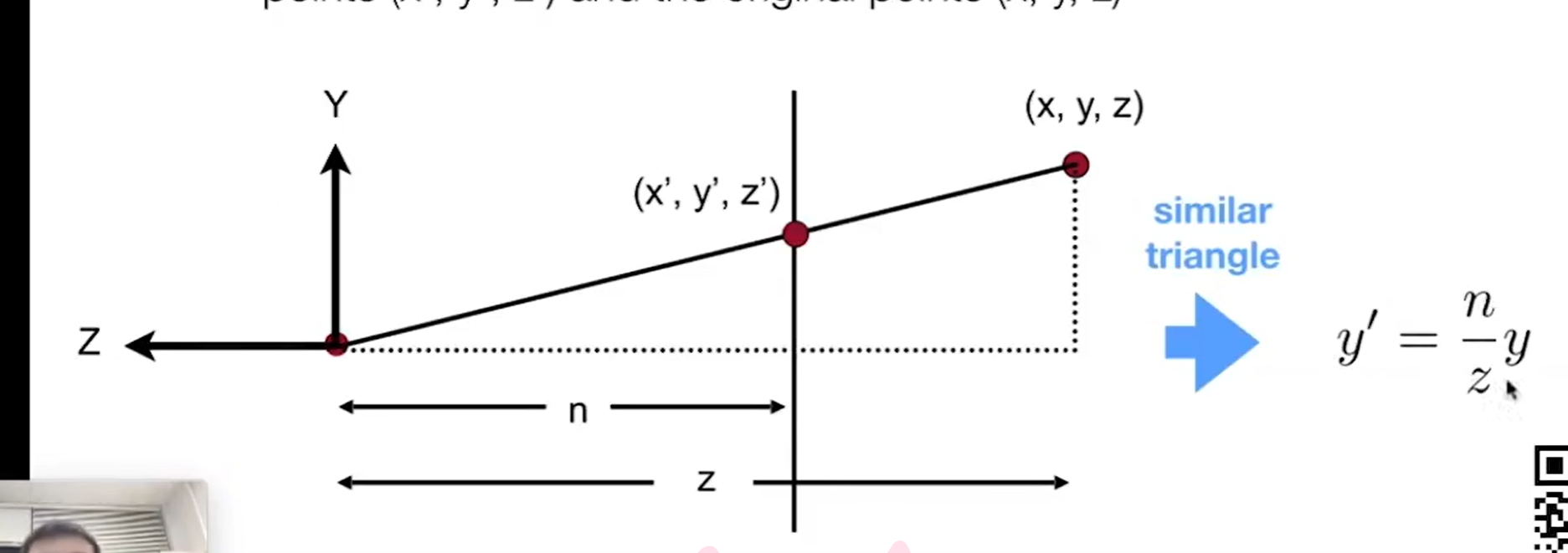
先看X,Y的变换情况，由上图可以得出x’ y’的变换情况，但是最重要的是不知道z坐标如何变换，可能变大也可能变小

解释：当我们确定好 x‘ y’ 后，有如下式，M（变换矩阵） X（x，y，z，1）=> （nx/z，ny/z，unknown，1），又因为齐次坐标中，同乘一个数，坐标不变，这里我们同乘z，可得（nx，ny，unknown，z）

下面我们就可以先填数：因为已知M是4*4的矩阵，可得第一行（n，0，0，0）
第二行（0，n，0，0） 第三行不知道 第四行（0，0，1，0）注意：这里可不是仿射变换，不要认为最后一行是（0，0，0，1）

近平面性质： 所有点不变，即乘M后仍然不变

这里我们取近平面的任意一点，做投影变换，由于点不会变，所以输入（x，y，n，1）得到的还是（x，y，n，1），然后将结果同乘n（这里z坐标为n），即（nx，ny，n2，n）这里是为了凑形式，我们就能得到第三行的等式（0 0 A B）*（x y n 1）为n2，原因是n2 一定与x，y无关，所以x，y均为0

远平面性质：中心点不变

即（0，0，f，1）输入后仍为（0，0，f，1），同理，同时乘z（这里的z坐标为f），又可以得到一个关系式
结果：

12.视锥参数

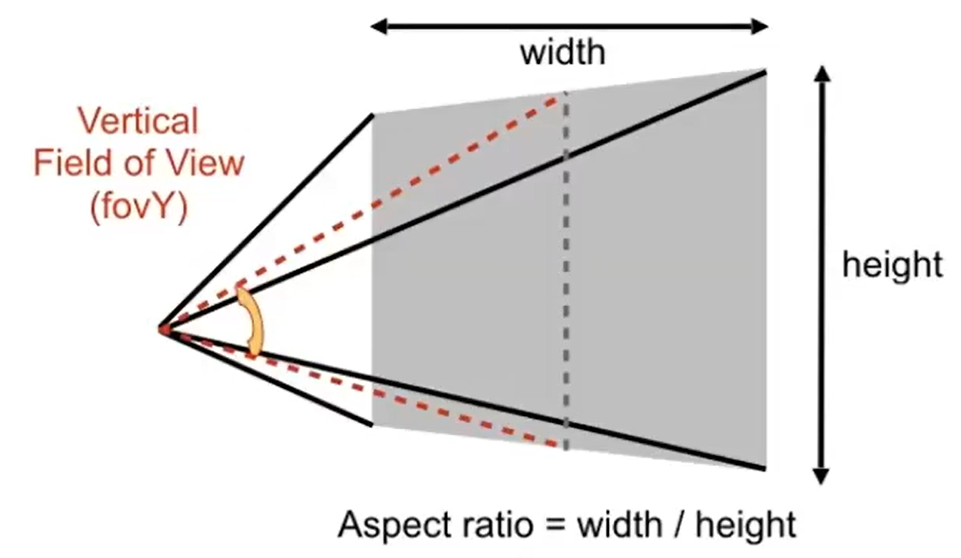
宽高比，fov角