Games101笔记 P2 rasterization

这是第二部分的内容，对应games101中P5-P6的内容

1.首先确定一个大概流程

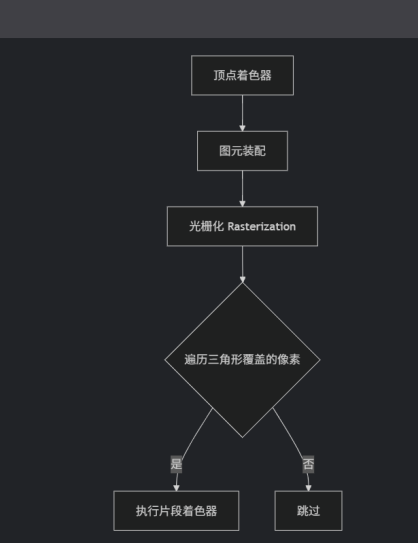
在P1中我们已经实现了MVP变换，对应在上图中表示为顶点着色器部分，图元就是三角形，线段等基础图形，图元装配负责将顶点组装成基本图元（点、线、三角形）。下面我们要学习光栅化阶段。

顶点着色器完整流程：

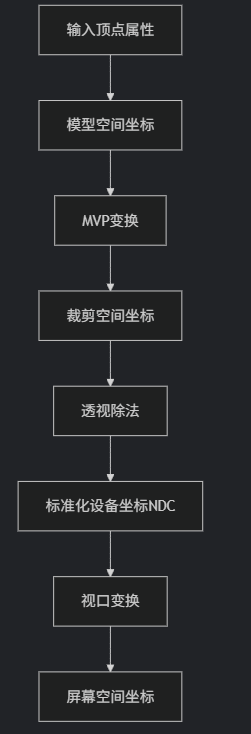
解释：一共分为五步

（1）输入顶点属性（顶点的位置，法线，UV等），此时处于模型空间坐标

（2）MVP变换，将顶点转换到裁剪空间坐标（顶点着色器负责的部分，也就是实现模型空间到裁剪空间的转换）

以下三步虽然在顶点着色器阶段，但已经不由顶点着色器实现

（3）裁剪，将视锥体外部的图元全部清除，只保留视锥体内部

（4）透视除法，将裁剪空间的大小，转换到[-1 1]的NDC坐标中

（5）视口变换，将[-1 1]区域，转换到屏幕大小区域。（此时是连续的，还没有像素的概念）

理解：

投影变换分为两种

-1 正交投影，这是特殊的投影，在P变换中，直接乘正交投影矩阵后，就能把成像区变为[-1 1 ]的裁剪空间坐标（正交投影不需要再做透视除法）。 但是后续还需要再做裁剪

重要：（需详解）

透视变换矩阵不是线性的！！！

-2 透视投影，假设有一个坐标如下（x_view,y_view,z_view,1）齐次坐标

先乘一个透视变形矩阵（P1中最后的那个矩阵）

注意，此时得到的结果为(x_dist,y_dist,z_dist,w_dist)最后一项不是1！我们知道一个坐标原本的形式最后一项应该为1

下一步，在乘一个正交投影矩阵

我们都知道正交投影矩阵的形式，在乘正交矩阵后，得到的W坐标也不是1，但是这就是透视投影的全部，他的输出是一个齐次坐标形式，且W坐标不为1。

然后就到了裁剪，透视除法（将W坐标归1，这里才最终变为NDC坐标）

2.屏幕的定义：

是一个二维数组，数组中的每个值代表一个像素

3.Rasterization：光栅化，将矢量图形（如三角形）转换为像素（栅格）的过程，本质是将连续的图形所包围的范围离散为像素。

4.屏幕空间的定义：

从左下角开始（0，0）那么右上角的坐标应为（width-1，height-1）

像素由其左下角的坐标决定。

像素中心的坐标为（x+0.5，y+0.5）

此屏幕覆盖的范围是（0，0）到（width，height）

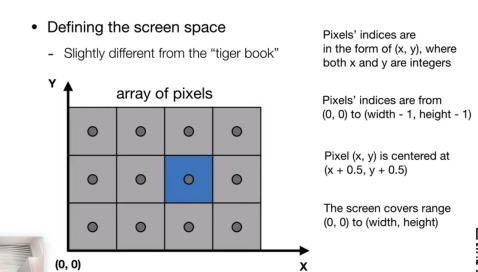
5.由NDC空间到屏幕空间的转化（视口变换）

我们已经得到了一个标准的立方体，如何将他变为屏幕空间？

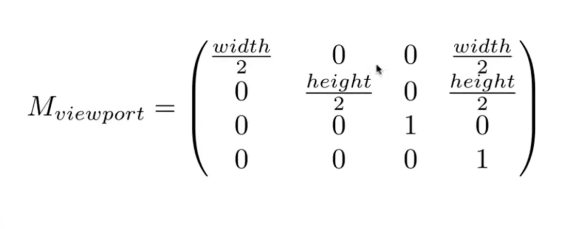
只需乘这个矩阵即可，Z坐标不用动，为后续Z-buffer使用

这个矩阵不要忘了先缩放在平移

注意：经过这个变换之后，我们得到的实际伤势width*height*1的长方体，我们还没有把他变成二维（但是可以看成二维了，深度值z用来进行深度缓冲）

6.光栅化的具体步骤

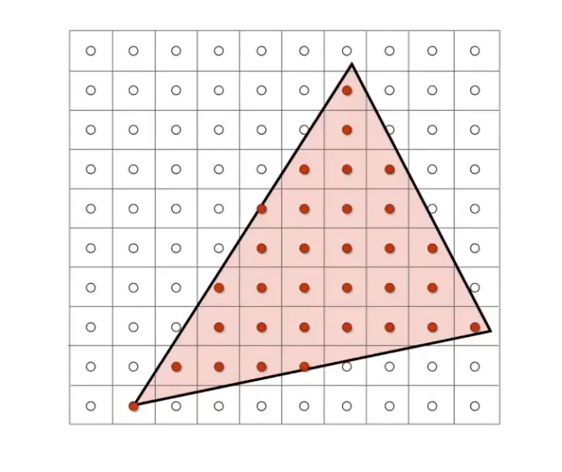
最重要的一点，如何将图元所包含的像素都找出来，也就是判断像素是否在三角形的内部

 方法：每一个像素的中心点与三角形的三条边做叉乘

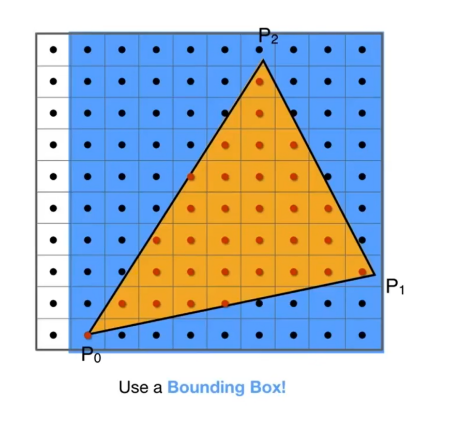
优化：由于每个像素都要与三角形做叉乘，这很费时间，所以我们可以将不可能在三角形内部的像素点先全部排除

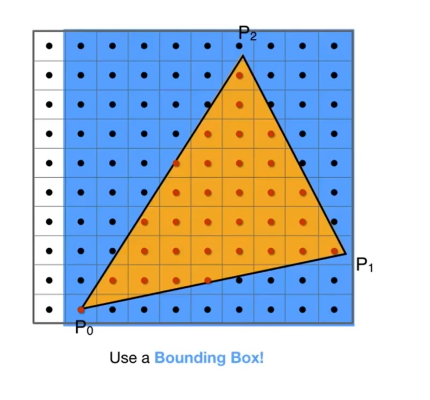
方法：AABB包围盒

最小x与最大x 最小y与最大y 形成的区域

7.采样/走样

采样产生的问题：锯齿、摩尔纹、车轮效应

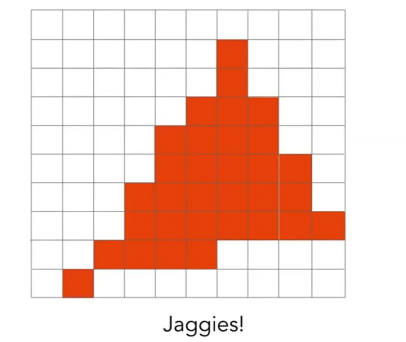
原因：信号变化的速度太快（频率太高），采样频率低，跟不上信号的变化

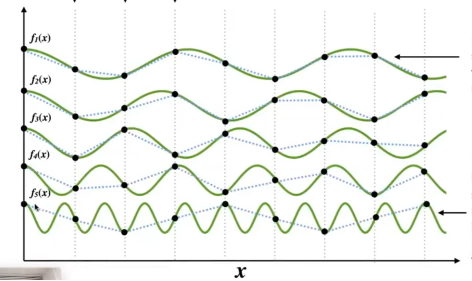
原理：高频信号若使用低频采样，则无法重建信号，会被错误的重建为低频

解决方法（即反走样）

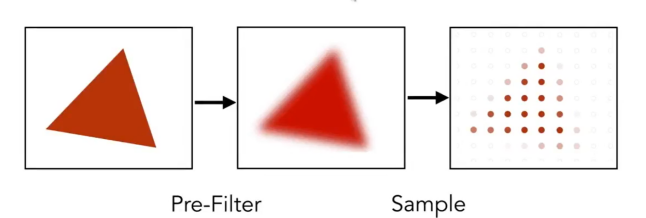
先模糊三角形，然后进行采样（先使用低通滤波，来过滤掉边缘的高频部分，然后对三角形进行采样）

解释：

首先，明确一点，使用模糊操作不会改变覆盖的像素，即原本三角形覆盖了哪些像素，仍然覆盖哪些像素

其次，抗锯齿（反走样）的本质是更改的是覆盖像素的权重

这里有一个区分，几何覆盖率（抗锯齿）的计算和着色计算（计算像素RGB）是独立的两个步骤，但最终会结合影响像素颜色。

下图为光栅化阶段与片元着色阶段

解释：每个片元（像素）携带着插值属性，即通过重心坐标计算的插值属性值

片元：理解为像素即可

覆盖率：在光栅化阶段形成，在片元着色阶段之后才会使用，着色阶段计算的是 “假设像素完全覆盖时的颜色”，覆盖率用于后续混合。

效果图

8.理解频谱图：

在上图中，右图为左图的傅里叶变换图，即从空间域转换到频域中，低频集中在中间，高频在四角（定义）。

在图像中，高频（图像颜色/亮度剧烈变化的区域）可以表示纹理密集的地方、人物的边界（背景与人物交界的地方）

示例：

高通滤波，即只留下高频信息，如人物边界等纹理密集的地方，低频信号被过滤，在频谱图上表示为中间变暗

低通滤波，只留下低频信息，模糊了边界，频谱图上四周都变暗

9.滤波=卷积=平均

解释：

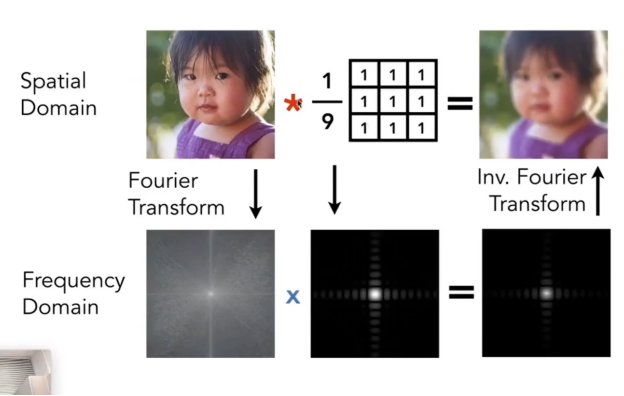
以上是一个3*3的box，即将9个像素加起来，然后求平均值，最后写入中间像素，所以在做完这个操作后，图像的边缘部分更加柔和，体现在图像上就是边界被模糊了（低通滤波）,在频谱图上也能够看出，高频信号减少了。

同时，时域的卷积等于频域的乘积，反之亦然（看下面两幅图）。

解释下面第二幅图：

第二幅图将表示为这种图像，即中间白色部分为盒子的大小，因为盒子是全1（即白），其频域图在右边

还有一个重要现象，盒子越大，相当于平均效果越强，那么频域图的高频部分就会越来越少。

10.在数学角度上对采样进行理解

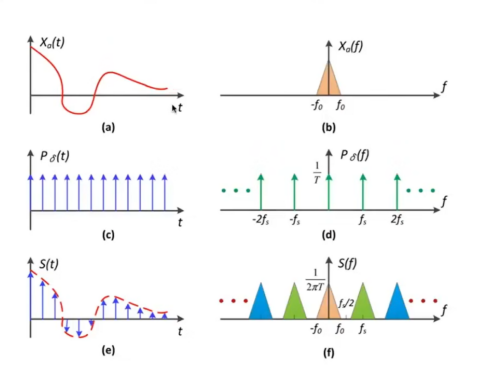
由上图我们可以得出以下信息

（1）x（t）的频谱图为X（f）

（2）采样是对时域上的函数乘一系列的冲激函数

（3）时域上的乘积等于频域上的卷积，在频域上，冲击函数的频谱仍为一系列的冲击函数（进行傅里叶变换即可），最后根据卷积的定义，可以得到频域上卷积一系列的冲击函数最终得到的结果是原频谱的周期延拓

理解了以上原理后，就能解释为什么会出现走样

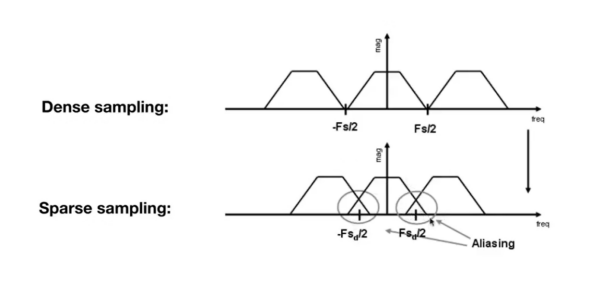
最终原理就是发生来了频谱混叠，当采样率不够高时，即采样越稀疏，频谱周期延拓的间隔就会越小，上图就发生了频谱混叠（走样）

11.如何进行反走样

（1）增加采样率，在计算机图形学中，增加采样率的方法就是换屏幕，将低分辨率的屏幕换为高分辨率的屏幕。这里侧面反映出，采样是以像素为单位进行的，当然，这里忽略了超采样技术。

结合这个图理解，当使用高分辨率的屏幕时，像素变多，那么采样率就会变高，进而减少锯齿

（2）先模糊在采样。

这里用频谱图来理解下，模糊即可去掉高频信息。以下去掉了高频信号后，频谱混叠消失。

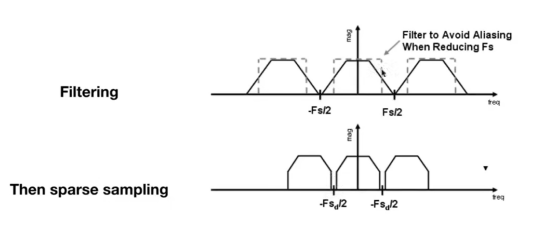
当我们不使用超采样技术时，可以使用卷积核（通常是3X3像素），进行模糊操作。

当我们使用了超采样技术（MSAA），下图是对一个像素中三角形占比多少进行平均，

12.超采样技术

MSAA：将一个像素分为多个子像素，然后求平均，得到覆盖率（注意：这相当于是实现模糊的一个操作，下一步是进行采样）

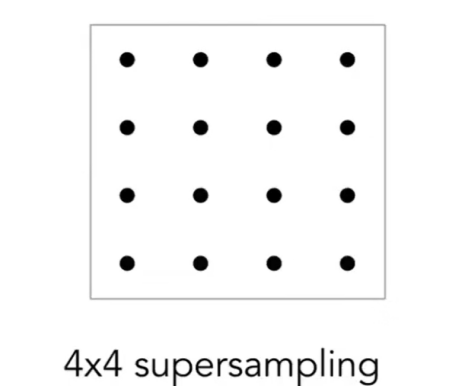
将一个像素分为16个小的像素，对这里面的点判断是否在三角形，然后求一个平均，就相当于对一个像素求了平均。

当然，划分为越多的小像素则结果更加精确，最理想的情况就是连续（即无限大）

13.深度测试

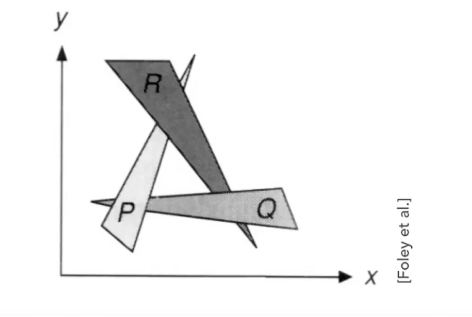
（1）画家算法：先将远处的物体光栅化出来，再将近处的物体光栅化出来

存在问题，无法准确判断复杂的遮挡关系

（2）深度缓存（Z-buffer）

会生成一副深度图，用来存储每个像素的最浅深度，通过最浅的深度，来判断遮挡关系，哪个物体应该在距离相机最近的地方

左边是渲染图，右边是深度图，越远深度越大，越白，越近深度越小，越黑

流程：

深度图的初始化深度为正无穷，即默认为无限远

先确定图元覆盖了哪些像素，然后对这些像素与深度图的存储的深度做比较，如果小于深度图存储的深度，则进行替换，将更小的深度信息填入深度图。

本质上深度缓存就是为了确定最终显示在屏幕上的是哪个图元所覆盖的像素