基于效能函数的无人机路径规划

基于效能函数的无人机感知数据采集路径规划算法

摘要

数据采集是无线传感器网络中最基本的任务之一。目前，传感器网络的信息收集方法主要包括静态信息收集方法和基于移动汇聚节点的信息收集方法。静态信息收集方法存在“能量空洞问题”。然而，在另一种方法中，汇聚节点的移动会受到环境地形的限制。因此，这两种方法在许多应用场景中难以长期有效地收集信息。为了解决上述问题，我们采用无人机从传感器网络中采集感知数据，并能够根据信息的重要性和需求程度选择信息采集的顺序。为解决无人机在实际环境中面临的能量限制以及数据采集时间延迟问题，本文构建了一个综合考虑数据价值、能耗、时间和风险的效率函数。提出了一种基于效率函数改进的A*路径规划算法，用于规划无人机在SDG节点之间的飞行路径。同时，还提出了一种蜂群路径规划算法，以解决SDG节点的节点分配与访问顺序问题。

关键词 ：无人机；无线传感器网络；数据采集；路径规划

1 引言

随着物联网技术的发展，物联网被广泛应用于智能交通[1],军事[2],农业生产[3],应急事务处理[4],救灾[5]和环境监测。各个方面的应用都离不开数据的采集。传感器网络作为物联网的载体，在物联网信息获取中发挥着重要作用。传感器节点从监测场景中采集的数据是物联网应用的关键部分，是感知层与应用层之间的纽带。如果没有数据被感知，物联网网络将失去其应用价值。因此，合理的数据采集方法至关重要。

目前，传感器网络主要通过汇聚节点进行数据采集。传感器节点通过一个或多个跳数将数据传输到汇聚节点。因此，靠近汇聚节点的节点比远离汇聚节点的节点发送更多的数据包。这导致靠近汇聚节点的节点能量迅速耗尽，最终造成整个网络中断，远程节点无法将数据发送到汇聚节点[6]。在[6]中，这种现象被称为“能量空洞问题”。在[7]中提出了一种基于移动汇聚节点的数据采集方法。该方法通过在监测区域内移动配备有汇聚节点的电动有轨电车来收集数据。

尽管“能量空洞问题”已得到解决，但当传感器网络部署在野外地形或悬崖、滑坡等危险区域时，汇聚节点无法在监测区域内移动。当传感器网络部署在脆弱生态环境保护区时，汇聚节点的移动可能会对环境造成破坏，因此通过移动汇聚节点收集数据并不可行。因此，可以利用无人机（无人飞行器）为这些特殊应用场景收集数据，它不仅可以解决“能量空洞问题”，还能摆脱环境地形的限制。

汇聚节点安装在无人机上。无人机在监测区域中导航并进行数据采集，以减少飞行距离、降低能耗和减少数据延迟。在[14]中，无人机与地面传感器节点之间的垂直距离等于或略小于最大有效通信距离，从而减少无人机的飞行距离并优化飞行路径。在[15]中，根据数据价值和数据相似性选择具有较大数据价值的关键节点，无人机仅采集关键节点的数据，从而大幅减少无人机的数据采集任务。在[16]中，为在确保无人机能够从每个传感器节点采集所需数据的同时最小化所有传感器节点的最大能量消耗，作者联合优化了传感器节点的唤醒调度和无人机的轨迹。在[17]中，通过部署协作中继，摆脱对簇头节点的限制，可以更自由地选择无人机飞行的航路点，使数据采集更高效并降低能耗。

上述文献主要使用单架无人机进行数据采集，但当监测区域范围较大且传感器节点数量较多时，单架无人机已无法在最大数据延迟和能量限制内完成所有传感器节点的数据采集。我们需要采用多架无人机进行数据采集，并规划其飞行路径，以使每架无人机都能在时间限制和能量限制内完成数据采集任务。

本文中，我们建立了一个效能函数来评估路径的质量。该效能函数考虑了数据价值、能耗、时间以及风险等因素。然后，我们采用改进的A*算法和蜂群算法来规划无人机在进行数据采集时的飞行路径。A*算法用于规划无人机从一个SDG（传感数据采集）节点到另一个SDG节点的飞行路径；利用蜂群算法将每个SDG节点分配给各个无人机，并确定数据采集顺序。

本文其余部分组织如下。第二节描述了效能函数。在第三节中，改进了 A*算法，并用于规划SDG节点之间的飞行路径。在第四节中，基于蜂群算法进行无人机飞行路径规划。第五节展示了性能评估与仿真结果。结论在第六节中给出。

2 效能函数

在规划多架无人机的飞行路径时，需要建立相应的评价指标来评估规划出的飞行路径的质量。本文采用效能函数作为评价指标。该效能函数考虑了数据价值、能耗、时间和风险等因素。

多架无人机在监测区域R内从无线传感器网络中采集数据。监测区域R内设有多个SDG（感知数据收集）节点，用于将传感数据传输给无人机。在无人机进行数据采集前，已知SDG节点的位置，以及每个SDG节点中传感器的类型、数量和数据价值。无人机在数据采集期间停留在SDG节点区域内，并与地面传感器通信以获取所有感知数据。无人机不得飞入禁飞区。

2.1 数据价值

无人机从每个SDG节点获取的数据价值取决于SDG节点中各类传感器的数量及相关数据价值。$v_y$ 是 $y$ 类传感器所感知数据的数据价值。因此，无人机在SDG节点 $i$ 处采集的数据价值为：

$$
D_{si} = \sum_{y=1}^{J} n_{yi} v_y \tag{1}
$$

$n_{yi}$ 是SDG节点中 $y$ 传感器节点的数量。

因此，无人机从SDG节点 $i$ 飞往SDG节点 $j$ 所采集数据的价值为：

$$
D_{ij} = \frac{1}{2}(D_{si} + D_{sj}) \tag{2}
$$

2.2 能耗

由于无人机能量有限，因此必须确保无人机在能量耗尽之前完成任务并安全返回目的地。无人机的能量主要用于飞行和悬停。

$d_{ij}$ 是SDG节点 $i$ 到SDG节点 $j$ 的距离。无人机飞行路径上每一点的能耗为 $f_e$，且 $f_e$ 与地形相关。因此，从SDG节点 $i$ 到SDG节点 $j$ 的飞行能耗为：

$$
E_{ij}^f = \int_0^{d_{ij}} f_e \, dl \tag{3}
$$

当无人机收集数据时，需要在SDG节点上空悬停一段时间。无人机在悬停过程中的能耗称为悬停能耗。我们假设无人机每单位时间悬停的能耗为 $h_e$。无人机在SDG节点 $i$ 处的悬停能耗为[8]：

$$
E_i^h = h_e t_s \sum_{y=1}^{J} n_{yi} n_d^y \tag{4}
$$

$n_{yi}$ 是SDG节点 $i$ 中的 $y$ 传感器节点数量。$t_s$ 是单个数据包的交换时间。$n_d^y$ 是 $y$ 传感器中数据包的数量。

因此，无人机从SDG节点 $i$ 飞往SDG节点 $j$ 的能耗为：

$$
E_{ij} = E_{ij}^f + \frac{1}{2}(E_i^h + E_j^h) \tag{5}
$$

2.3 时间

无人机主要将时间花费在飞行和悬停上。$\bar{v}_{ij}$ 是从SDG节点 $i$ 到SDG节点 $j$ 的无人机平均飞行速度，因此从SDG节点 $i$ 到SDG节点 $j$ 的飞行时间是：

$$
T_{ij}^f = \frac{d_{ij}}{\bar{v}_{ij}} \tag{6}
$$

无人机在SDG节点 $i$ 上悬停的时间为：

$$
T_i^h = t_s \sum_{y=1}^{J} n_{yi} n_d^y \tag{7}
$$

因此，无人机从SDG节点 $i$ 飞往SDG节点 $j$ 的时间为：

$$
T_{ij} = T_{ij}^f + \frac{1}{2}(T_i^h + T_j^h) \tag{8}
$$

2.4 风险

当无人机飞行和悬停时，可能会面临风险。我们将无人机在飞行过程中遇到的风险称为飞行风险。无人机飞行路径上每个点的飞行风险为 $r_f$，因此从SDG节点 $i$ 到SDG节点 $j$ 的飞行风险为：

$$
R_{ij}^f = \int_0^{d_{ij}} r_f \, dl \tag{9}
$$

无人机在SDG节点上方悬停以收集数据的风险，我们称之为悬停风险，SDG节点的悬停风险为：

$$
R_i^s = r_{ih} t_s \sum_{y=1}^{J} n_{yi} n_d^y \tag{10}
$$

$r_{ih}$ 是单位时间内悬停的风险。

因此，无人机从SDG节点 $i$ 飞往SDG节点 $j$ 的风险为：

$$
R_{ij} = R_{ij}^f + \frac{1}{2}(R_i^s + R_j^s) \tag{11}
$$

2.5 效能函数与约束

$M$ 是用于数据采集的无人机数量，用于对多架无人机进行编号。表示为 $F = {f_1, f_2, …, f_M}$。因此，第 $m$ 架无人机数据采集的飞行路径为 $P_m = {S_0, S_i, S_j…, S_0}$。为了定义效能函数并描述约束条件，定义如下 0-1 决策变量：
$x_{ijm}$：当第 $i$ 个和第 $j$ 个SDG节点位于第 $m$ 条无人机数据采集路径上时为1，其余为0。

第 $m$ 个无人机的相关参数如下：

数据价值：

$$
D_m = \sum_{i=0}^{N} \sum_{j=0}^{N} D_{ij} x_{ijm} \tag{12}
$$

能耗：

$$
E_m = \sum_{i=0}^{N} \sum_{j=0}^{N} E_{ij} x_{ijm} \tag{13}
$$

时间：

$$
T_m = \sum_{i=0}^{N} \sum_{j=0}^{N} T_{ij} x_{ijm} \tag{14}
$$

风险：

$$
R_m = \sum_{i=0}^{N} \sum_{j=0}^{N} R_{ij} x_{ijm} \tag{15}
$$

所有无人机相关参数如下：

总数据值：

$$
D_{ma} = \sum_{m=1}^{M} D_m \tag{16}
$$

总能耗:

$$
E_{ma} = \sum_{m=1}^{M} E_m \tag{17}
$$

总时间:

$$
T_{ma} = \sum_{m=1}^{M} T_m \tag{18}
$$

总风险

$$
R_{ma} = \sum_{m=1}^{M} R_m \tag{19}
$$

多无人机数据采集的效能函数如下：

$$
U_m = a \cdot \frac{D_{ma}}{D_{\text{max}}} + b \cdot \frac{T_{ma}}{T_{\text{max}}} + c \cdot \frac{E_{ma}}{E_{\text{max}}} + d \cdot \frac{R_{ma}}{R_{\text{max}}} \tag{20}
$$

$D_{\text{max}}$、$T_{\text{max}}$、$E_{\text{max}}$、$R_{\text{max}}$ 是预先设置的各参数的最大值。

多无人机数据采集的限制如下：
确保每架无人机在有限时间和能量耗尽之前完成所有SDG节点的数据采集。因此存在能量和时间约束：

$$
\max(E_m) \leq E_{\text{max}}, \quad \max(T_m) \leq T_{\text{max}} \tag{21}
$$

确保每个SDG节点的数据都被收集：

$$
\sum_{j=0}^{N} x_{ijm} = 1, \quad i \in S \
\sum_{i=0}^{N} x_{ijm} = 1, \quad j \in S \tag{22}
$$

每架无人机都保证从起点出发，最终返回终点。

$$
P_m(0) = S_0, \quad P_m(\text{end}) = S_0 \tag{23}
$$

确保每架无人机都将收集数据，没有无人机处于空闲状态。

$$
\sum_{i=1}^{N} \sum_{j=1}^{N} x_{ijm} \neq 0, \quad m \in M \tag{24}
$$

3 基于A*算法的无人机在SDG节点间的飞行路径规划

在本节中，我们使用A*算法来规划无人机从一个SDG节点到另一个SDG节点的飞行路径。首先，对监测区域进行栅格化，然后创建一个开放列表以记录已评估区域的邻域。使用关闭列表来记录已经被评估过的区域，并计算从“起点”到“目标点”的估计距离，关闭列表保存所有已被探索或评估的节点。在路径寻找过程中，根据评估函数扩展节点。开放列表和关闭列表中的节点随时发生变化，同一节点可能在开放列表和关闭列表中重复出现。根据评估函数找到终点后，再通过回溯方式获得从起点到终点的最终路径。

3.1 评估函数

$$
f(n) = k \cdot (g(n) + h(n)) + (1 - k) \cdot \text{cost}(n) \tag{25}
$$

$g(n)$ 是从起点到当前点的距离，当节点 $n$ 位于节点 $n−1$ 的垂直或水平方向时，使用公式(26)计算；当节点 $n$ 位于节点 $n−1$ 的对角方向时，使用公式(27)计算：

$$
g(n) = g(n−1) + 1 \tag{26}
$$

$$
g(n) = g(n−1) + 1.4 \tag{27}
$$

$h(n)$ 是一种启发式函数，表示从当前节点到终点的估计距离，A*算法通常使用欧几里得距离来表示 $h(n)$：

$$
h(n) = \sqrt{(x_n − x_{\text{end}})^2 + (y_n − y_{\text{end}})^2} \tag{28}
$$

$\text{cost}(n)$ 是当前节点的飞行代价：

$$
\text{cost}(n) = \frac{\text{UAVrisk}(n)}{\text{UAVrisk} {\text{max}}} + \frac{\text{UAVenergy}(n)}{\text{UAVenergy} {\text{max}}} + \frac{1}{\text{UAVvelocity}(n)} \cdot \frac{1}{t_{\text{max}}} \tag{29}
$$

3.2 评估函数中k值的确定

k值表示评估函数中飞行代价的权重值。使用A*算法规划的飞行路径会因k值的不同而不同。

为了评估由A*算法规划的无人机飞行路径的好坏，我们定义从SDG节点 $i$ 到SDG节点 $j$ 的飞行消耗为：

$$
\text{flycon} = \frac{E_{ij}}{E_{ij}^{\text{max}}} + \frac{T_{ij}}{T_{ij}^{\text{max}}} + \frac{R_{ij}}{R_{ij}^{\text{max}}} \tag{30}
$$

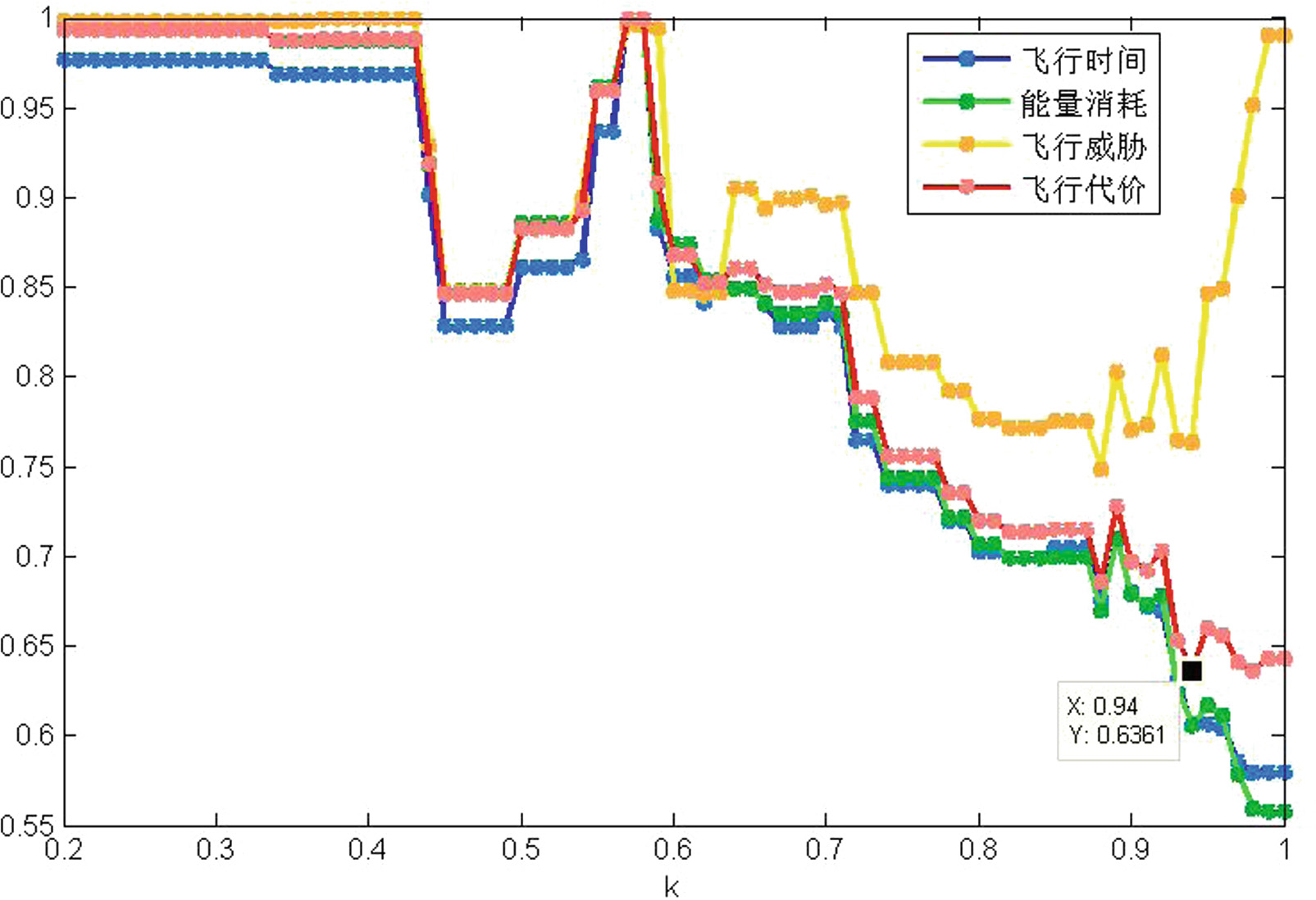
为了更充分地展示k值对规划路径的影响，我们展示了图1中的时间、能耗、风险和飞行消耗。

从图1可以看出，当k大于0.6时，能耗和时间随着k的增大趋于减少。因为k值越大，评估函数中距离的权重越大，规划路径的长度将缩短，从而减少无人机的能量消耗和时间。风险先减小后增大，因为k值越大，评估函数中风险的权重越小，其对结果的影响也越小。规划路线搜索距离越短，风险值越高。该区域因此会导致飞行风险增加。

图3、4、5、6、7、8、9和10中标记的节点为飞行能耗的最小值。此时飞行能耗为0.6361，对应的k值为0.94。通过改变起点和终点的位置，我们发现当飞行能耗为最小值时，对应的k值主要分布在0.92−0.96范围内。因此，我们确定k值为0.94。

3.3 A*算法与Dijkstra算法的比较

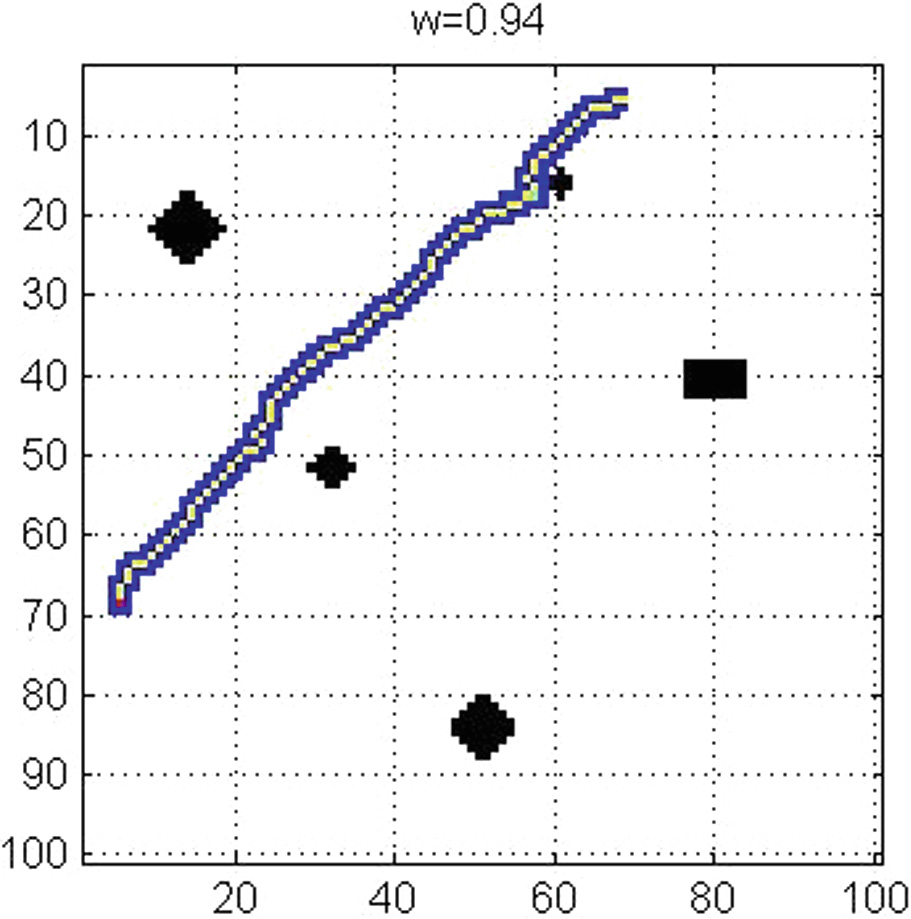
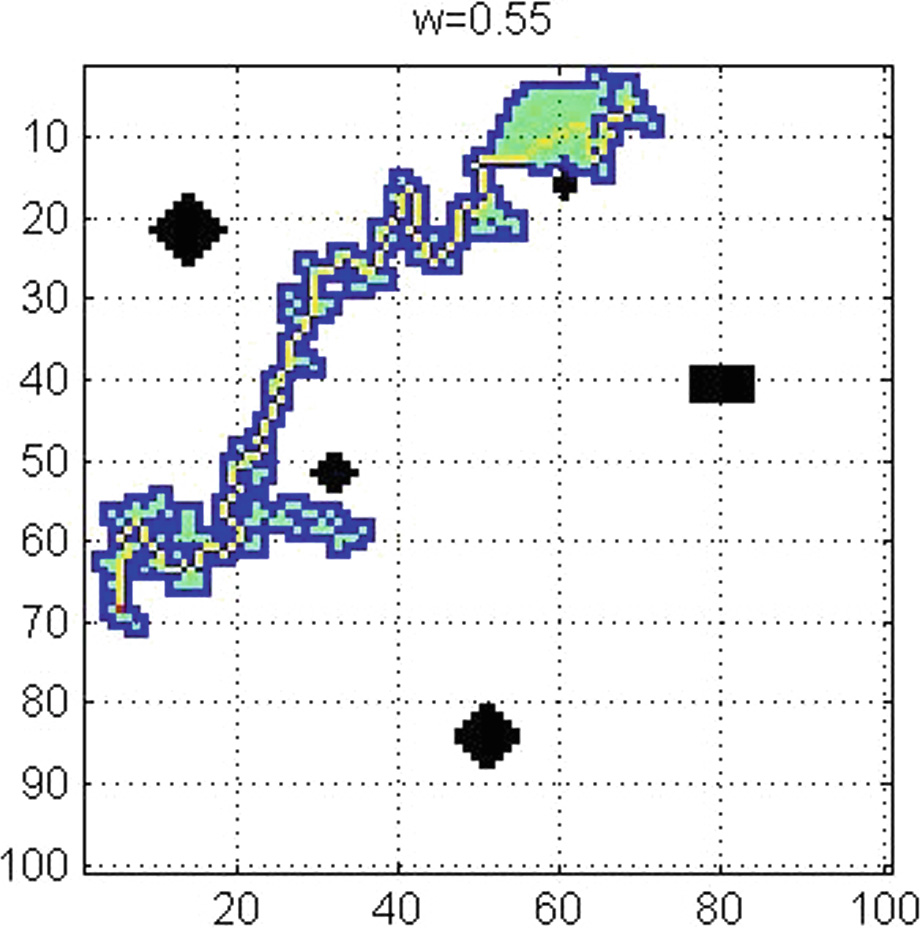
为了验证改进的A*算法的性能，我们将A*算法与Dijkstra算法进行比较。我们在区域R中选择一个起点和一个终点，并分别绘制从起点到终点的A*算法和Dijkstra算法的搜索范围图。

从图2和图3可以看出，改进的A*算法的搜索范围远小于Dijkstra算法的搜索范围，因此可以在更短时间内获得最优路径。并且改进的A*算法的路径更直。由于无人机难以进行大范围机动，无人机无法按照Dijkstra算法规划的路径飞行，因此改进的A*算法规划的路径更加合理。

4 基于蜂群算法的无人机飞行路径规划

我们使用蜂群算法将每个SDG节点分配给各个无人机。无人机之间交换SDG节点并调整收集SDG节点数据的顺序，以使所有规划路径的总效能值最大化。

在蜂群算法中，蜜蜂被分为三类：引领蜂、跟随蜂和侦察蜂。每个引领蜂对应一个蜜源（一个可行解）。引领蜂根据邻域策略生成新的蜜源，评估新旧蜜源的效能值，采用贪婪策略进行选择，并以一定概率将该信息共享给其他蜜蜂。跟随蜂根据蜜源的效能值以一定的概率选择要跟随的引领蜂，并在其邻域内搜索其他蜜源，尝试改变所跟随引领蜂的蜜源，以获得更大的效能值。当某个蜜源在有限的搜索时间后无法进一步改进（即该蜜源已被充分利用）时，该蜜源将被舍弃，对应的蜜蜂将转变为侦察蜂，侦察蜂将在搜索范围内随机生成一个新的蜜源。

4.1 初始解的生成

我们以三架无人机和十个SDG节点为例生成初始解。无人机编号为1、2和3。SDG节点编号为1、2、3，…9和10。在每一组初始解中，每架无人机随机选择一个SDG节点作为第一个数据采集节点。每个SDG节点只能被选择一次，然后根据每架无人机的前一个SDG节点，在剩余未选节点中找到相对于前一个SDG节点的效能函数值最大的节点。以此方式生成n组初始种群（表1）。

第一架无人机	第二架无人机	第三架无人机
0-5	0-1-6-8-0	0-7-9-10-0
		0-3-2-4-0

4.2 邻域搜索策略

邻域搜索策略是基于已生成的解，通过某些操作改变解以获得新解的策略。本文采用反转策略、最近策略和交叉策略进行邻域搜索。

a. 反转策略
无人机路径中两个不同随机位置的SDG节点被反转。

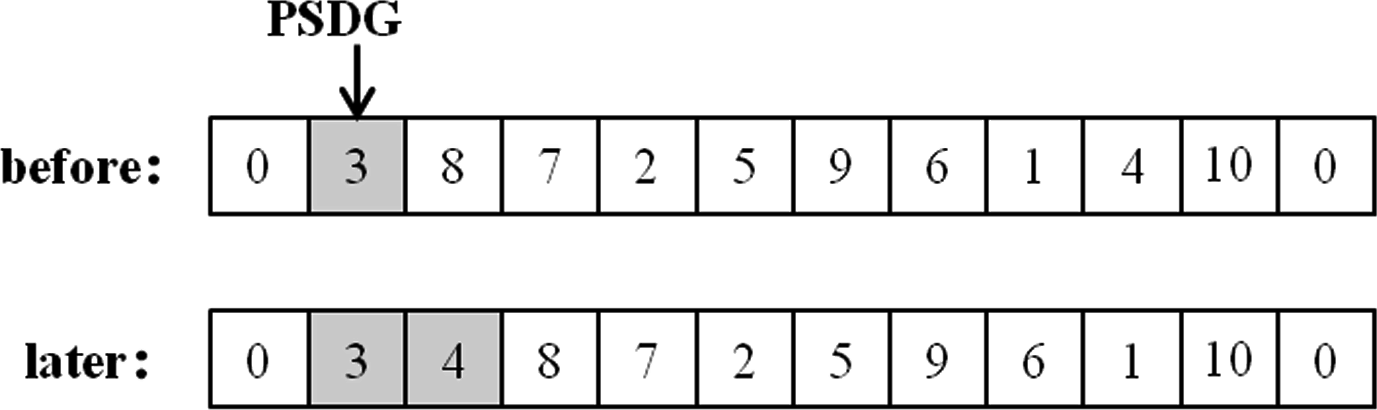
b. 最近策略
在路径字符串中随机选择一个SDG节点，我们称其为PSDG，然后选择一个与PSDG效能值最高的SDG，并将其插入到PSDG之后。

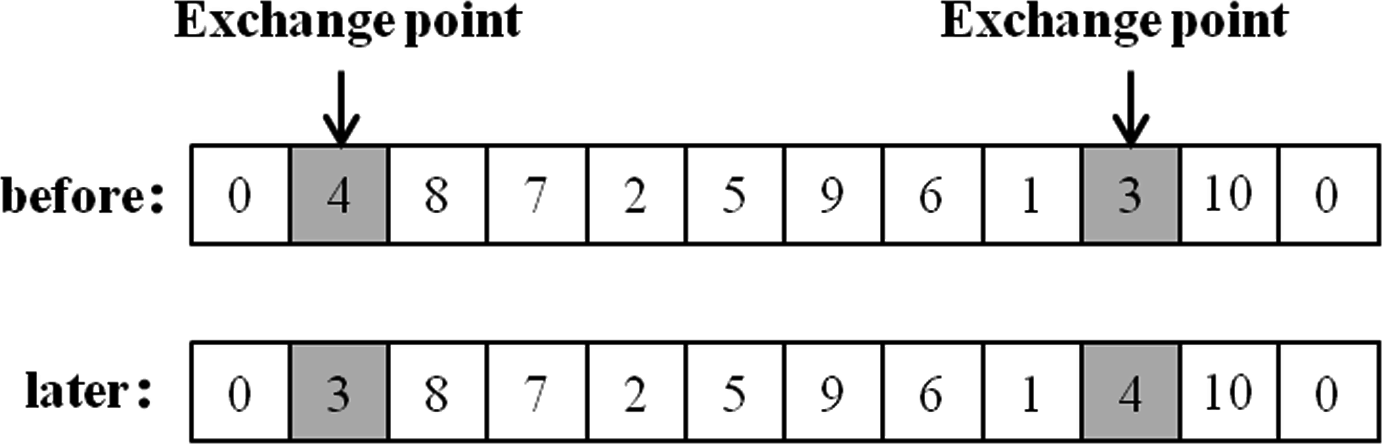
c. 交叉策略
我们从同一组解的两条无人机路径中随机选择一段进行交换。

5 仿真分析

5.1 初始参数设置如下（见表2）

参数	符号	数值
第i个SDG节点中的y传感器数量	$n_{yi}$	0–5
y传感器的数据价值	$v_y$	1–3
速度	$v$	8–13 米/秒
能耗	$f_e$, $h_e$	10–20
Risk	$r_f$	0–1
时间限制	$T_{\text{limit}}$	30分钟
能量限制	$E_{\text{limit}}$	4000

5.2 仿真步骤

步骤1：输入初始参数。
步骤2：使用A*算法规划SDG节点之间的路径。
步骤3：利用蜂群算法将SDG节点分配给每架无人机，并确定无人机数据采集的顺序。
步骤4：对规划路径进行平滑处理。
步骤5：绘制数据采集路径图并输出仿真结果。

5.3 仿真结果

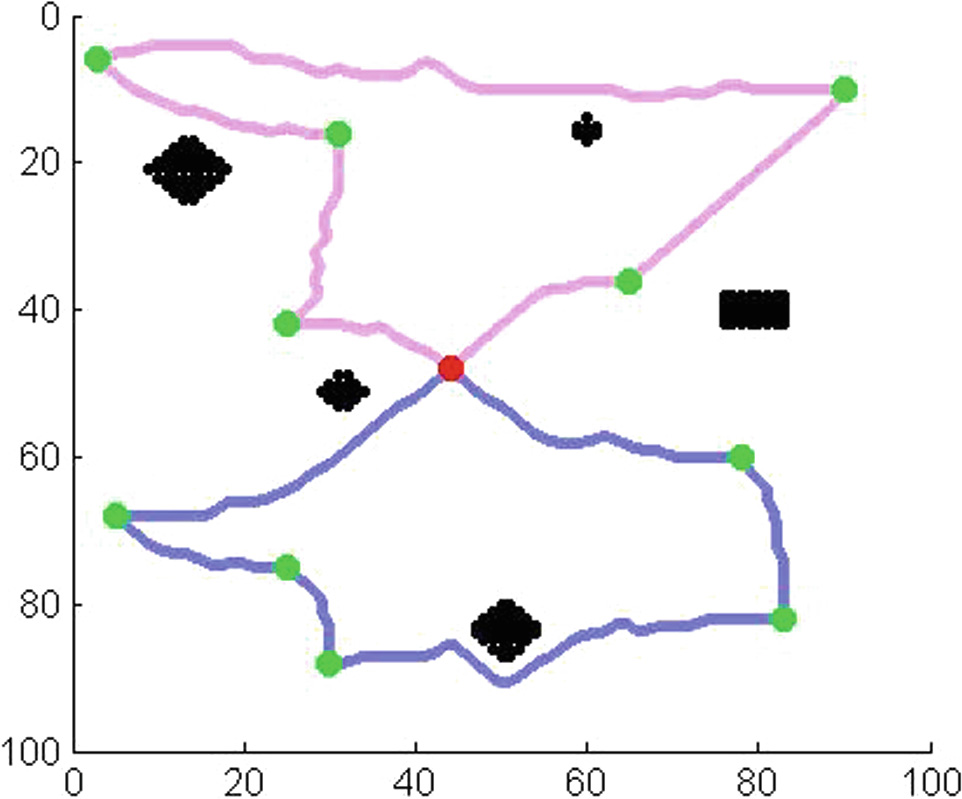
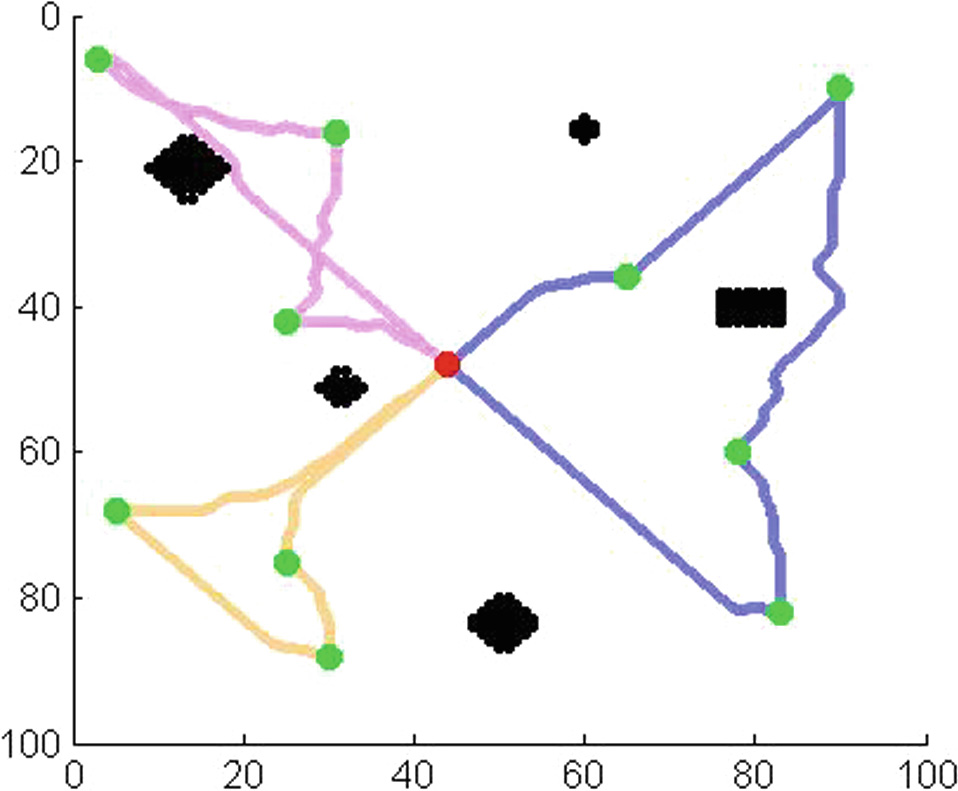
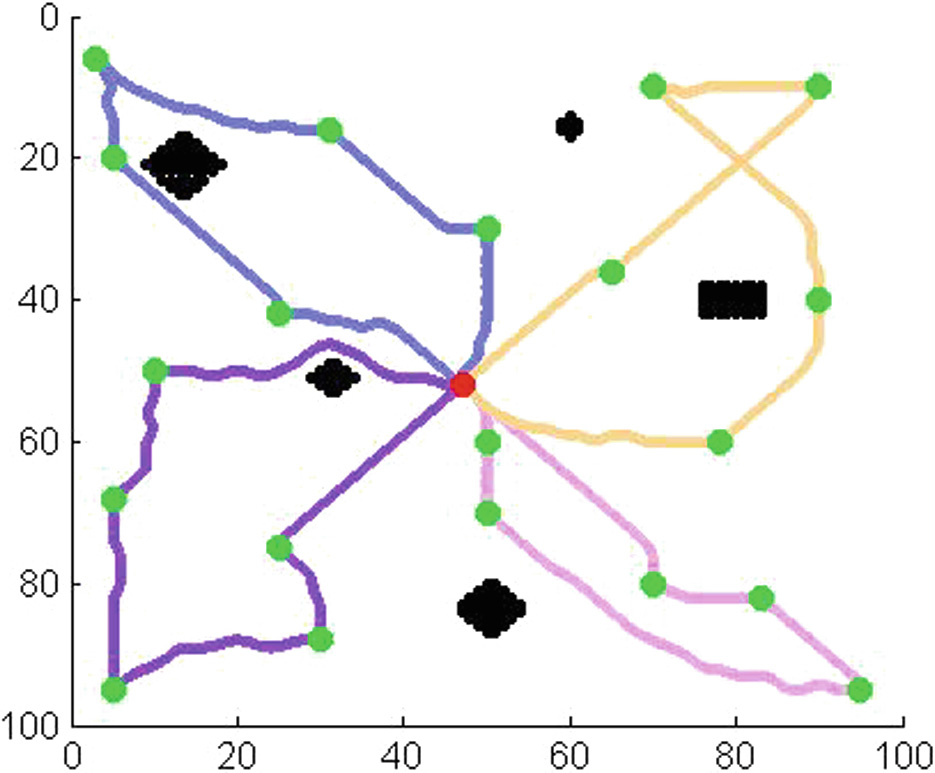
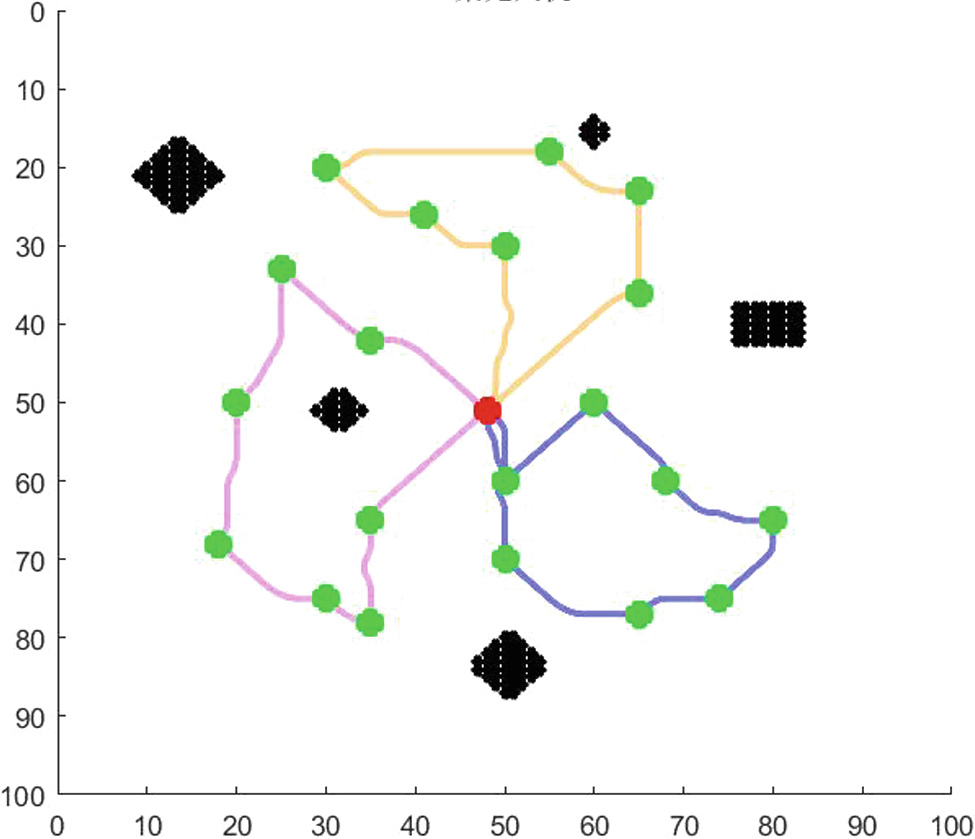
本节将展示使用多架无人机从SDG节点收集数据时的路径规划结果。图7、8、9、10、11、12、13和14展示了使用不同数量的无人机从不同数量的SDG节点收集数据的路径规划结果。图13展示了起始节点不在目标区域中心时的路径规划结果。图14展示了SDG节点相对集中时的路径规划结果。红点为起点（终点），绿点为SDG节点，黑色区域为禁飞区。不同颜色的线条为不同无人机的飞行路径。

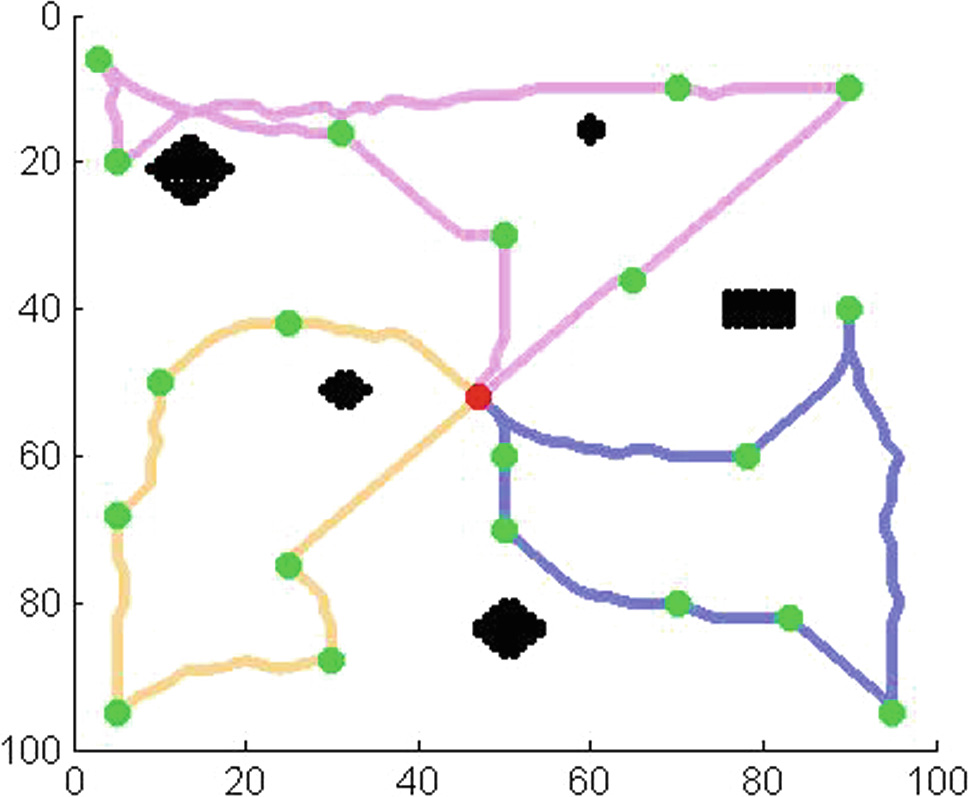
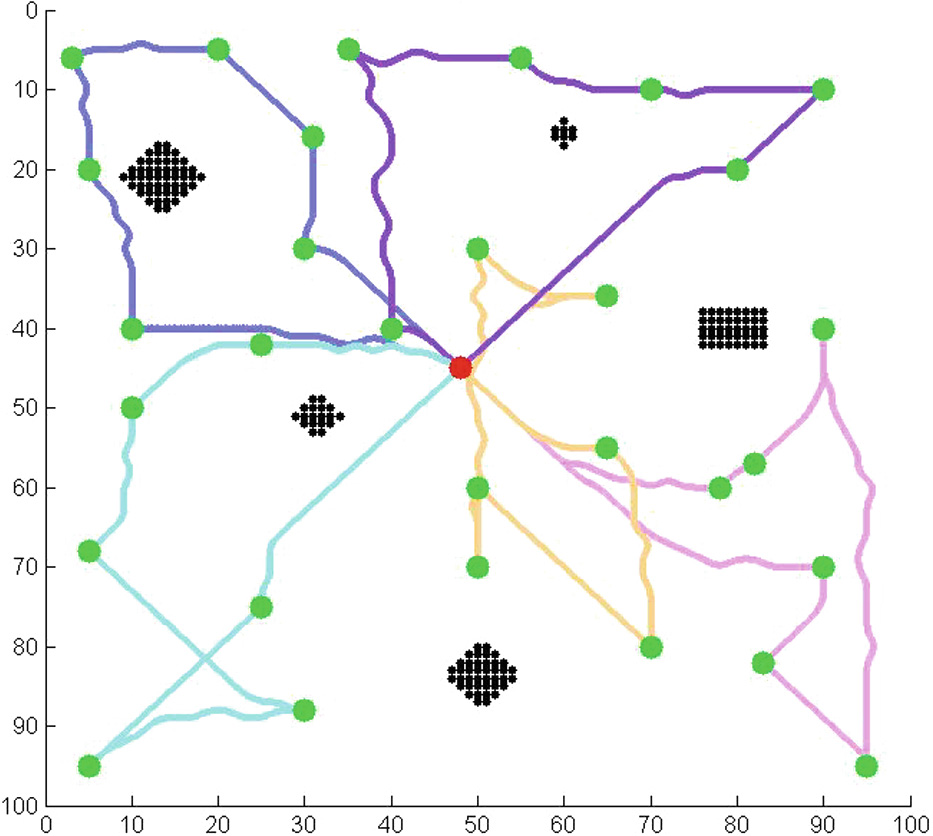
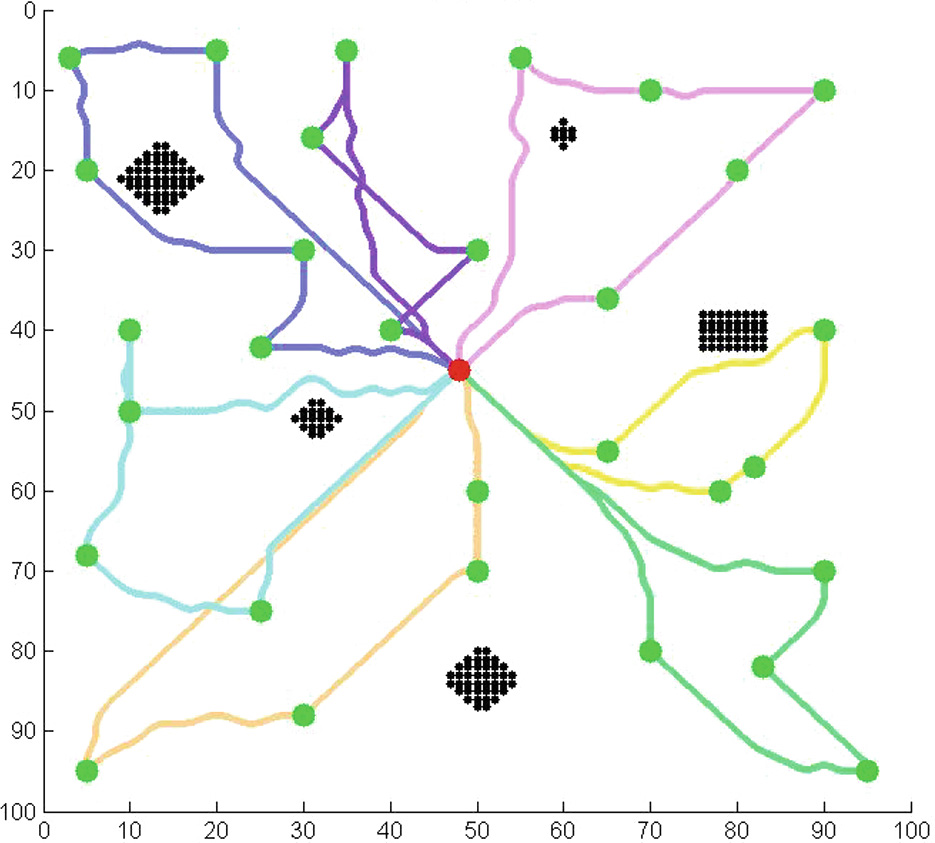
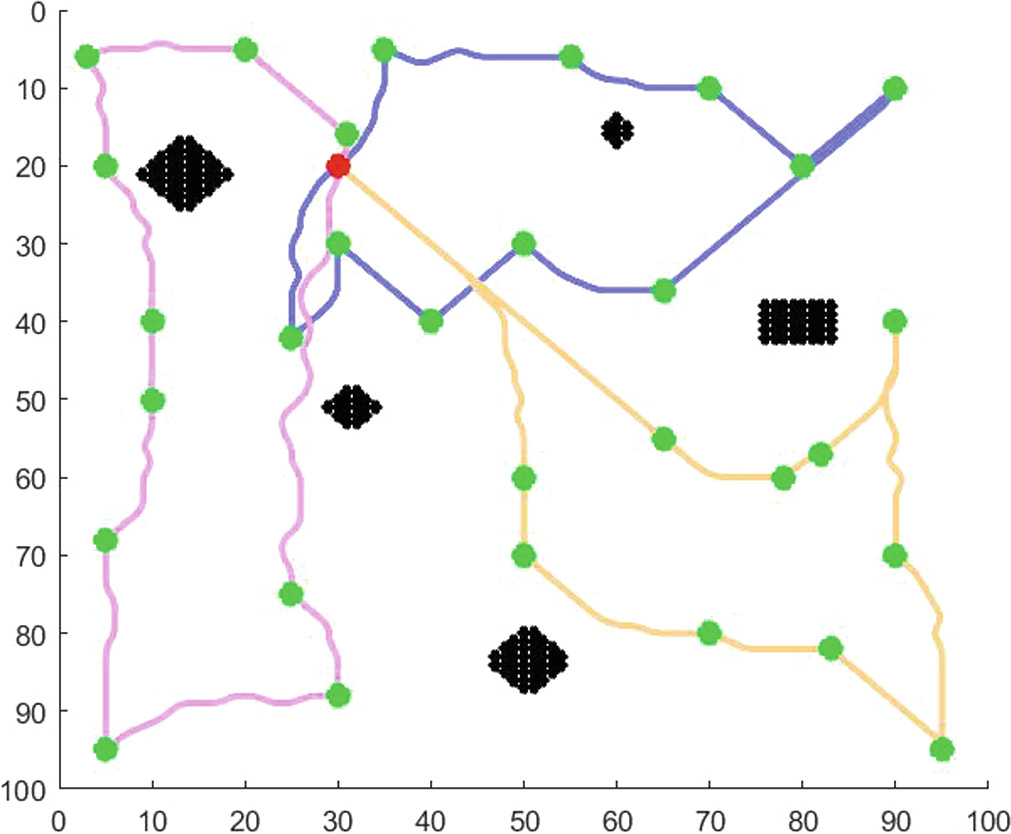
为了进一步分析使用不同数量的无人机对效能函数值的影响，我们使用1–7架无人机从20个SDG节点收集数据，并获得总能耗、总时间以及总风险。结果如表3和4所示。

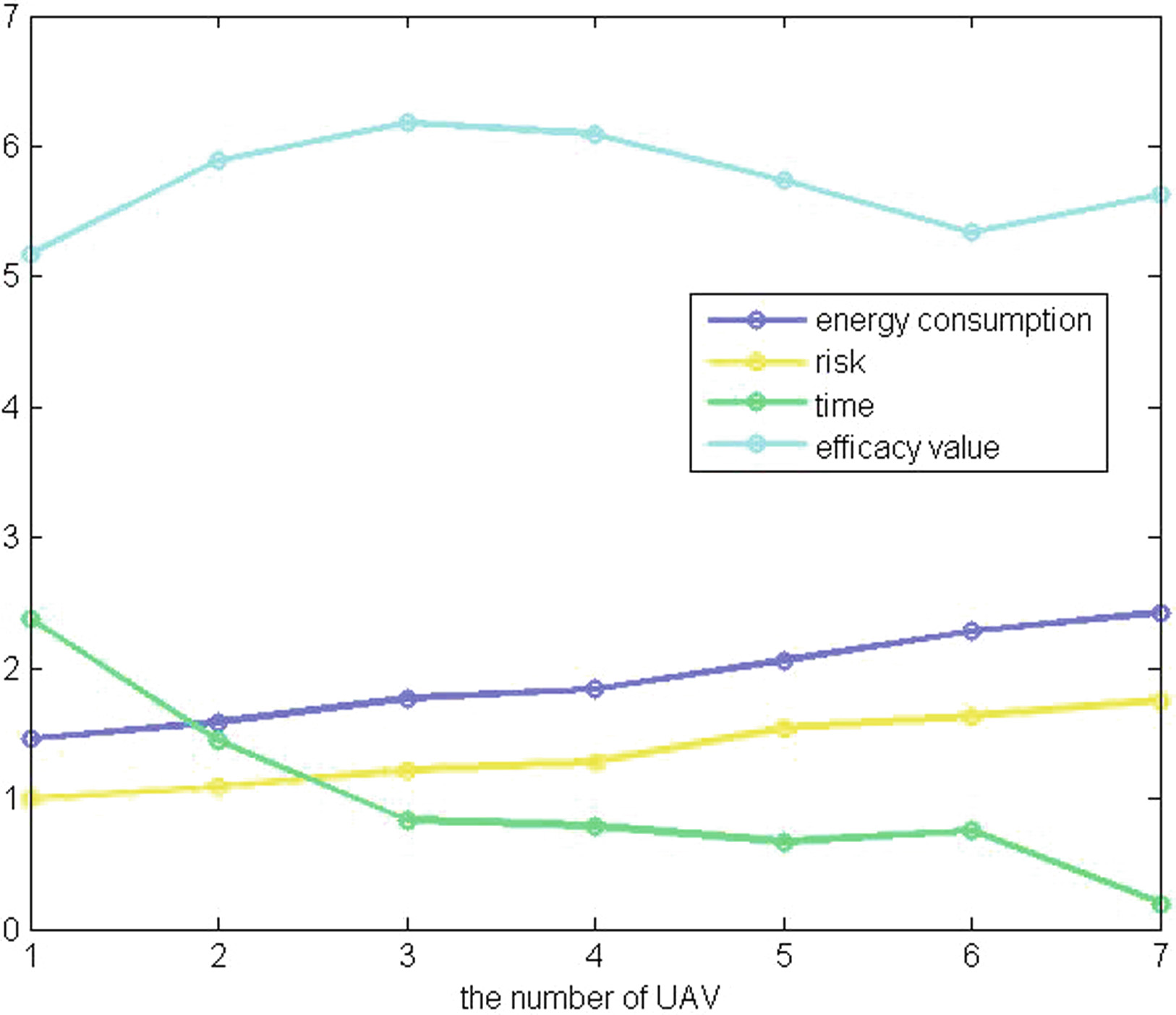
为了进行对比分析，每个参数在图15和16中展示。

表3. 效能函数仿真结果参数（初始点位于目标区域中心）

无人机数量	总能量消耗	总风险	总时间(s)
1	5829.4	119.32	4279.1
2	6340.6	130.43	2595.3
3	7062.2	146.59	1501.4
4	7340.6	153.43	1430.3
5	8243.4	184.72	1199.7
6	9120.2	195.40	1351.0
7	9694.0	210.77	347.9

表4. 效能函数仿真结果参数（初始点不在目标区域中心）

无人机数量	总能量消耗	总风险	总时间(s)
1	5691.6	118.54	4212.3
2	6803.8	133.75	2389.6
3	7791.2	154.50	1913.8
4	8481.8	171.55	1720.7
5	9495.2	186.90	1123.3
6	10593.6	208.74	1096.3
7	11371.0	220.48	754.5

)

)

从图15可以看出，总能耗随着无人机数量的增加而增加，因为每架无人机都需要从起点出发并最终返回起点，因此总飞行距离会增加，无人机的总能耗也随之增加。风险值的变化趋势与能耗相似。随着飞行距离的增加，无人机在飞行过程中的风险可能性也在增加，因此风险值随着无人机数量的增加而增大。

由于无人机数量的增加，每架无人机需要采集的SDG节点数量减少，因此每架无人机的飞行距离更短，所需时间也更少。由于每架无人机同时从起点出发，完成任务并返回起点的最后一架无人机的飞行时间即为本次数据采集的时间值。

从图15可以看出，效能值先增大后减小，当无人机数量为三架时达到最大值。当仅使用一架无人机进行数据采集时，能耗和风险值最小，但单架无人机的最大飞行时间和最大能量消耗已被超过，因此效能函数值较低。当使用七架无人机进行信息采集时，所需时间最短，但由于无人机数量较多，需要消耗大量能量，且风险值也较大，因此效能函数值也较低。当使用三架无人机进行数据采集时，虽然各项参数均未达到最小值，但时间大幅缩短，能耗和风险值的增加较小，因此效能值最大。

从图16可以看出，当初始节点不在目标区域中心时，能耗、风险和时间的变化趋势与图15所示相同，但使用两架无人机时数据采集的效能值最大。因为当初始节点不在目标区域中心时，无人机需要飞行较长的距离才能到达SDG节点所在区域。因此，使用的无人机数量越多，无人机在没有SDG节点的情况下飞行的总路径长度就越长，从而导致无人机消耗更多的能量和时间。

从上述图表和分析可知，当初始节点位于目标区域中心时，最好使用3架无人机从20个SDG节点收集信息；当初始节点不在目标区域中心时，最好使用2架无人机从20个SDG节点收集信息。

6 结论

本文提出了一种用于广域物联网传感器网络中无人机数据采集的算法。建立了效能函数以评估路径质量，该效能函数考虑了数据价值、能耗、时间和风险等因素。采用A*算法规划无人机从一个SDG（感知数据收集）节点到另一个SDG节点的飞行路径。利用蜂群算法将每个SDG节点分配给每架无人机，并确定数据采集顺序。最终，通过多架无人机获得了数据采集的路径规划结果。仿真结果表明，该方法能够优化无人机飞行路径、降低能耗，并为多无人机数据采集提供依据。