基于DRL的车载边缘计算卸载

面向车载边缘计算的深度强化学习：一种智能卸载系统

1 引言

随着普适系统和智能车辆的快速发展，作为信息物理系统（CPS）子集的基于人工智能的车载网络[37],已引起越来越多的关注。全球许多研究人员一直在致力于开发新型汽车应用，以创造更加舒适和安全的驾驶环境。然而，如何在车辆上执行这些计算密集型应用仍面临巨大挑战，例如，如何基于车对车（V2V）和车对基础设施（V2I）通信模式实现车辆与网络服务器之间的实时反馈；如何为资源受限应用提供高效计算能力，以及为车辆和基础设施提供合理的资源分配。

最初，研究人员提出了移动云计算（MCC）的范式[40],将丰富的计算和存储资源集中到云服务器中。尽管其具有强大的计算能力，但仍难以满足车载应用的实时响应需求。因此，移动边缘计算（MEC）是一种有前景的替代方案，其节点靠近用户。与MCC相比，MEC可以显著降低通信延迟，而通信延迟在车载网络中会随着路由跳数的增加呈指数级增长[8]。此外，MEC节点的多样性显著挖掘了网络中的潜在计算资源，同时也减轻了中心基站（BS）的工作负载[4]。值得注意的是，除路侧单元（RSUs）外，任何具备计算、缓存或网络功能的实体都可以作为MEC的平台。由于资源受限，MEC节点的能力受到限制，传统耗时且耗能的网络方法在车载网络中的性能可能会急剧下降[3, 5]。因此，迫切需要为MEC环境开发一种高效的解决方案。

深度强化学习（DRL）是一种有望替代传统方法的前瞻性技术。近年来，机器学习在图像处理、模式识别和自然语言处理等多个领域取得了显著成果。它也被应用于计算密集型应用程序，包括通过V2V或V2I实现的自动驾驶和实时导航。然而，在支持MEC的车载网络（即车载边缘计算）中，机器学习仍处于起步阶段。一些研究尝试利用深度学习和卷积神经网络来预测交通流量。然而，DRL很少被考虑。为了构建一个适用于车载边缘计算的智能卸载系统并使其良好运行，存在三个主要挑战：

(1) 尽管深度强化学习在雅达利游戏和围棋中取得了巨大成功[17],但其在车载网络中的应用几乎不存在。这是因为车载网络高度动态，且卸载系统中的约束比国际象棋的明确规则更加隐性、灵活和多样化。(2) 深度强化学习和传统车载网络都是基于一系列捕获的图像进行研究的。然而，在我们的智能卸载系统中并不存在连续图像。如何在没有图像的情况下将深度强化学习迁移到车载网络中是一个相当具有挑战性的问题。

(3) 无论是在国际象棋还是雅达利游戏中，深度强化学习模型通常只有一个“智能体”。由于多辆车辆参与智能卸载系统，因此很难构建合适的环境并建立相应的深度强化学习模型。

在本文中，将深度强化学习方法与车载边缘计算相结合，以解决计算任务卸载问题，联合研究车载网络中的任务调度和资源分配优化。首先，分别对通信架构和边缘计算架构进行建模。信道状态和计算能力是随时间变化的有限连续值，下一时刻的状态仅与前一时刻相关。为了便于分析，将其离散化并量化为多个级别，并进一步建模为有限状态马尔可夫链（FSMC）[30]。此外，我们通过离散随机跳跃对车辆移动性进行建模。路侧单元与车辆之间的接触次数服从泊松分布，其中参数表示移动强度。随后，建立了车载网络中流量调度和资源分配的联合优化问题。由于所建立的问题受到多种因素约束且变量之间相互耦合，我们将原始问题分解为两个子优化问题。对于第一个子问题，通过设计效用函数来确定多辆车辆的优先级，反映用户的用户体验质量水平。第二个子问题被建模为一个强化学习（RL）问题，分别阐述了四个关键要素：智能体、系统状态、动作和奖励。主要贡献总结如下：

(1) 基于有限状态马尔可夫链，我们联合研究车载网络中的任务调度与资源分配，并构建一个智能卸载系统。具体而言，将深度强化学习与车载边缘计算相结合。我们建立了一个优化问题，旨在最大化用户体验质量，同时兼顾能耗和执行延迟。(2) 由于所提出问题的高复杂性，将其分解为两个子优化问题。在第一阶段，我们对多辆车辆的任务进行调度。定义了一个效用函数来量化用户体验质量水平。提出一种双边匹配方案来求解该子问题，以最大化总效用。(3) 在第二阶段，通过利用深度强化学习算法解决资源分配的决策问题。通过应用Dropout正则化和双深度Q网络改进深度Q网络，以应对过高估计的缺陷。我们在深度强化学习模型中确定了系统状态、动作和奖励函数，其目标是通过获得最优策略来最大化累积奖励。(4) 性能评估表明了我们所设计系统的有效性，即所提出的双边匹配方案能够高效地逼近穷尽搜索方案的性能，且改进后的深度强化学习算法在不同系统参数下优于其他方法。

本文其余部分组织如下：在第2节中，我们回顾相关工作。第3节描述系统模型。第4节中，我们建立优化问题。第5节介绍所构建的智能卸载系统。为解决两个子优化问题，第6节给出了两种算法。第7节提供了性能评估，第8节总结了我们的工作。

2 相关工作

近年来，基于深度学习和边缘计算的CPS引起了众多研究人员的关注。我们回顾了三个类别，包括基于深度学习的CPS、基于MEC的CPS以及深度学习在MEC中的应用。由于CPS包含各种网络系统，我们选择车载网络作为示例，介绍最近的研究进展。

2.1 基于深度学习的信息物理系统

深度学习通常用于模式识别和交通预测。参考文献[18]利用无监督学习对城市智能卡数据进行聚类，涵盖以站点为中心和以乘客为中心的视角。采集法国雷恩大都市区的真实数据，以分析交通流量分布及乘客之间的相似性。设计了一种协作神经网络，用于在真实交通场景中基于捕获的图像构建结构化车道检测系统[13]。首先，设计了一个深度卷积网络来检测交通标志及其几何属性。其次，处理信号空间分布的循环神经网络难以被明确识别。在捕获数百万张交通图像后，如何高效检索这些海量数据成为一个具有挑战性的问题。为此设计了一种有监督哈希编码方案，用于生成高质量二进制码[35]。采用卷积神经网络分析图像的特征表示。量化损失函数确保相似图像被编码为相近的二进制码。参考文献[1]采用基于长短期记忆（LSTM）的循环神经网络来预测实时出租车需求。与传统预测方法不同，他们不预测确定性的值，而是利用混合密度网络预测出租车需求的概率分布。参考文献[16]提出了一种新的神经网络训练方法。该方法考虑了时空相关性以预测交通流量。该训练方法的核心思想是采用逐层贪婪无监督学习方案对深度神经网络进行逐层预处理，从而显著减少训练时间。

2.2 基于MEC的CPS

文献[28],构建了一个基于张量的协作式移动计算系统，其中云服务器负责处理大规模长期数据（如全局决策），MEC服务器负责处理小规模短期数据（如实时响应）。文献[36],提出了一种CPS流数据处理模式，通过聚类边缘设备以分布式方式提供网络服务。针对基于MEC的信息物理系统，文献[7]的作者联合研究了三个成本效益问题，包括基站关联、任务调度和虚拟机部署。为最小化总体成本，他们将优化问题建模为混合整数非线性规划问题，并将其线性化为混合整数线性规划问题。近年来，基于MEC的车载网络中的任务卸载已得到广泛研究。文献[20],为车载网络设计了一种基于非正交多址接入的任务卸载方案，利用频谱复用和高效计算技术来提高传输速率和卸载效率。文献[27]提出了一种车载网络中的三层实时交通管理系统，同时考虑了停放和行驶车辆，并将行驶车辆建模为M/M/1队列。优化目标是最小化平均响应时间。

2.3 深度学习在移动边缘计算中的应用

深度学习与移动边缘计算的集成已成为一个热门研究领域。参考文献[15]中提出了一种深度学习方法，用于在区块链网络中寻找边缘计算资源的最优拍卖方案。该方法设计了一种单调变换函数以对出价进行匿名化处理。采用softmax函数和relu函数分别计算获胜概率以及网络资源的价格。参考文献[34]中考虑了剩余电池容量和可再生能源因素，提出了一种基于决策后状态的强化学习算法。

将计算功耗和绿色能源充电分为两个阶段，并在中间状态进行自动扩展分配。提出了一种基于强化学习的演进型NodeB选择算法，该算法综合考虑了阻塞概率、通信速率和负载均衡[14]。为了减少网络中重复内容的数量，文献[10]中设计了一种面向智慧城市缓存的深度强化学习方法。系统中的智能体收集MEC服务器和基站的状态信息，并学习选择最优动作，以获得资源分配的最佳策略。文献[9]中的作者研究了设备到设备通信及网络通信中的社交属性，并设计了一个用于网络与计算的基于信任的社交网络框架。

据我们所知，针对车载边缘计算中深度强化学习的研究较少。尽管参考文献[23]和[11]研究了基于深度强化学习的网络与缓存，但我们的工作聚焦于车载网络中的计算卸载任务调度与资源分配，实现了用户服务质量体验与服务器收益之间的良好权衡。

3 系统模型

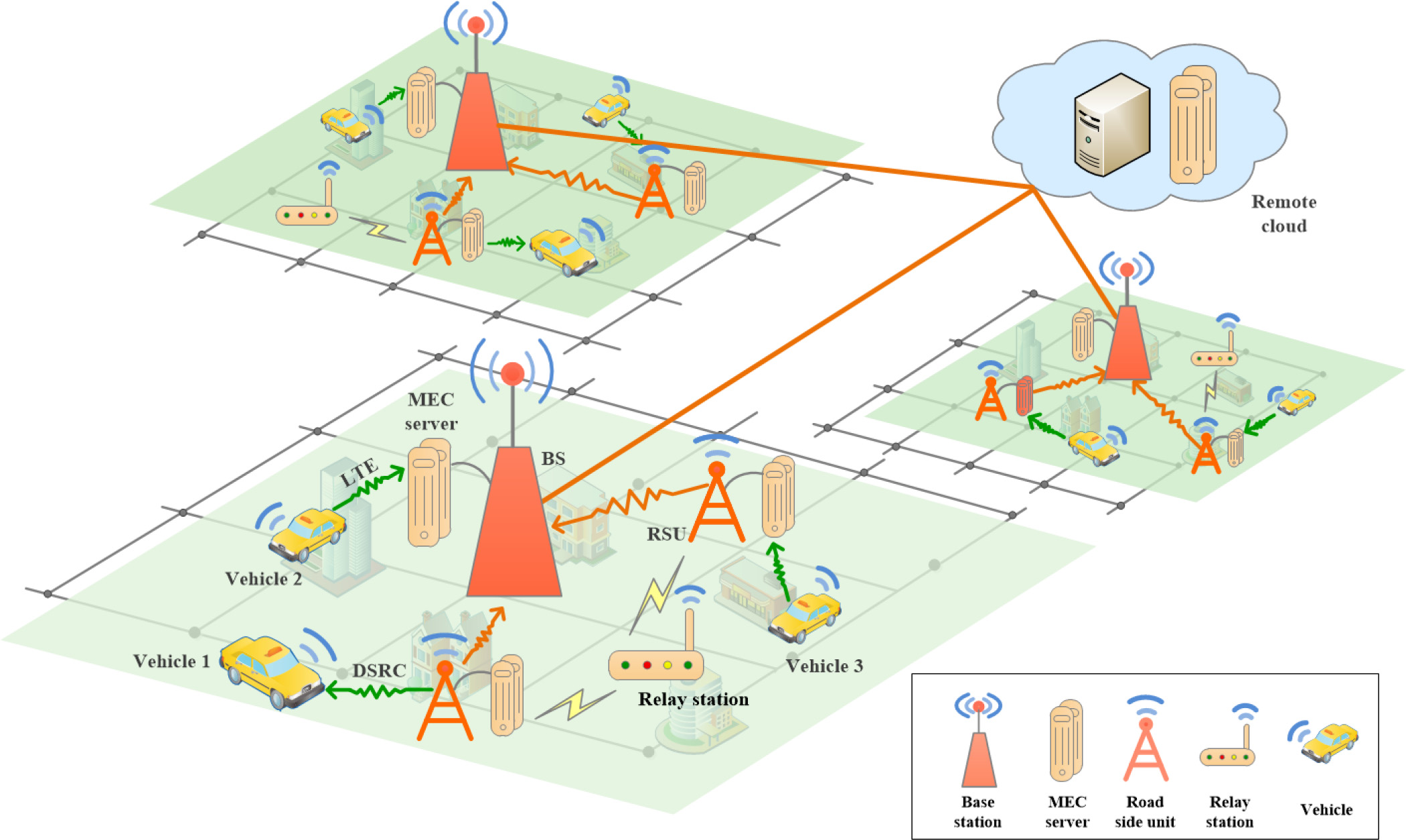
如图1所示，城市级车载网络可以根据街道或其他标准划分为多个区域。每个区域内有一个具有丰富计算资源的中心基站。车辆可以通过长期演进技术（LTE）与基站通信。类似于参考文献[19, 41],，我们假设蜂窝网络可以完全覆盖城市区域。此外，每个区域内的道路上部署了若干路侧单元。注意，路侧单元配备了MEC服务器。车辆基于专用短程通信（DSRC）向路侧单元上传任务，确保短距离内特别是单跳通信的高质量通信。路侧单元通过中继节点相互连接[31]，并通过中继站获取车辆任务卸载的全局信息。如果路侧单元仅与车辆和基站通信，则基站必须承担交通管理中心的角色，导致通信和处理负担巨大。

为了便于描述，我们考虑城市区域中的一个区域，该模型可以轻松扩展到其他区域。我们考虑一个基于区域的车载网络，包括一个基站、K个路侧单元和U辆车辆。借助MEC服务器的计算资源，路侧单元可以分担基站的计算任务，从而有助于缓解基站的过载并降低通信延迟。设 K={0, 1,…，K}和 U={1,…，U}分别为路侧单元和车辆的集合。我们假设，当车辆处于路侧单元的通信范围内时，仅通过单跳DSRC将任务上传至路侧单元；而位于路侧单元通信范围之外的车辆则可将任务上传至基站。

我们假设每辆车花费一段时间上传其卸载任务。令 T为通信持续时间，该时间可分为 Ti个时隙。车辆可将其任务卸载至基站或路侧单元。设ai, k(t)表示在时隙t内车辆、路侧单元和基站之间的连接关系，其中ai, k(t) = 1表示车辆i在时刻t连接到路侧单元k；否则ai, k(t) = 0。注意，k= 0表示选择基站进行连接。每个车辆在每个时隙只能连接一个路侧单元或基站，因此应满足以下约束条件：

$$
\sum_{k \in K} a_{i,k}(t)= 1,\forall i \in U. (1)
$$

整个网络由一个中央控制器运营，例如传统的移动网络运营商。网络运营商提供路由、缓存和计算服务，并从中获取利润。因此，在用户（即车辆）的用户体验质量与运营商利润之间存在权衡。我们研究的目的是找到最优的调度策略，在保证网络运营商收益的同时，最大化车辆的用户体验质量。

车辆移动性描述如下。尽管车辆随机移动且位置频繁变化，但在短时间内其位置变化相对较小。在离散时间段内，车辆的移动可视为从一个位置跳跃到下一个位置的离散图像。因此，我们通过离散随机跳跃来建模车辆移动性，相应的强度由跳跃间的平均停留时间表征。设Mi, k表示在通信时间Ti内路侧单元k与车辆i之间的连接次数，该次数服从参数为λ i, k的泊松分布。其中，λ i, k可视为连接频率，用于反映移动强度。

每当一辆车辆进入或离开RSU的无线覆盖范围时，会向该RSU发送一条消息，以强制该RSU更新其管理列表，RSU通过传输包含可用计算资源信息的消息来响应车辆。请注意，当MEC服务器过载时，RSU可能会发送服务拒绝消息。总通信时间Ti可分为两部分：RSU连接时间TR i和基站连接时间T B i。

3.1 通信模型

依赖基站，随着任务数量的增加，传统网络服务不可避免地导致高延迟。为了克服这一通信瓶颈，利用移动边缘计算来减少车辆与服务器之间通信的往返时间。此外，路侧单元之间的信息共享也可以减轻基站的通信负担。考虑到车辆与基站/路侧单元之间的无线连接是时变且无记忆的，我们将信道状态建模为有限状态马尔可夫信道。有多个参数可以决定通信速率，其中信道增益反映信道质量。令变量 γ k i 表示车辆i与路侧单元k之间无线链路的信道增益。实际上，真实的无线信道增益是一个连续变量。在我们的模型中，γ k i 的取值范围被离散化并量化为L个等级。令L={ϒ0,. . . , ϒL−1}表示马尔可夫链的状态空间： ϒ0，如果 γ ∗ 0 γ k i < γ ∗ 1 ； ϒ1，如果 γ ∗ 1 γ k i < γ ∗ 2 ；. . . ； ϒL−1，如果 γ k i γ ∗ L−1 。进一步地，信道增益 γ k i 在时隙t的实现值用 Γk i(t)表示。我们定义 Γk i(t)从一个状态дs转移到另一个状态hs的转移概率为ψд s ,hs(t)。这里дs和hs是 γ k i 的两个状态，属于 L。因此，我们可以得到车辆i与路侧单元k之间通信的如下L × L信道状态转移概率矩阵：

$$
\Psi_k^i(t)=[\psi_{д_s , h_s }(t)]_{L×L} , (2)
$$

其中 ψд s ,h s( t)=Pr (Γ k i(t+ 1) = h s | Γ k i(t)=дs)，且 дs，h s ∈ L。

正交多址接入（OMA）中有限的频谱资源尚未得到充分高效利用[21]。为解决这一问题，非正交多址接入（NOMA）被提出作为5G无线网络的一种有前景的解决方案，有望结合基于LTE的车联网（V2X）服务与蜂窝网络架构，并降低端到端延迟[6]。NOMA允许车辆非正交地接入基站，即多辆车辆可以在同一信道上并发上传数据，从而提高频谱效率。

由于每个路侧单元一次仅接入一辆车辆，而基站可以同时为多辆车辆提供服务，因此我们认为车辆与路侧单元之间的链路采用正交频分多址接入（OFDMA）技术，车辆与基站之间的链路则采用非正交多址接入（NOMA）技术。因此，车辆与路侧单元通信时不存在干扰。在时隙t的瞬时数据传输速率可计算如下：

$$
υ_{i, k}(t)= b_{i, k}(t) \log_2\left(1+ \frac{p_{i, k}(t)(\Gamma_k^i(t))^2}{\sigma^2}\right), (3)
$$

其中，bi, k(t) 表示从路侧单元k到车辆i正交分配的带宽，k ∈K且i ∈ U。令 B表示该区域内总可用带宽。因此，∑i∈U,k ∈K bi, k(t) B。变量pi, k(t) 表示车辆i的发射功率，σ 2为高斯白噪声功率。

为了应对多辆车辆之间信道共享引起的干扰，终端接收器（即基站）可以采用连续干扰消除（SIC）[24]。因此，基站于时隙i在时隙t接收到的来自车辆的信号可计算为：

$$
y_{i,0}(t)= \sqrt{p_{i,0}(t)}\Gamma_0^i(t) x_{i,0}(t)+ \sum_{n≠i, n∈U} \sqrt{p_{n,0}(t)}\Gamma_0^i(t) x_{n,0}(t)+ \sigma, (4)
$$

其中x和y分别表示车辆发送的信号和基站接收的接收信号。公式(4)中yi,0的第一部分来自目标车辆的有效信号；第二部分是共享该信道的其他车辆产生的干扰信号；第三部分是噪声。

接收信号后，基站根据信道增益的降序采用SIC解码方案，以减少来自其他车辆的干扰[38]。例如，存在两辆车ui,uj ∈ U。如果 γ 0 i > γ 0 j ，则基站将uj视为对ui的干扰，并在解码后将其消除。当基站解码uj时，已无干扰。即对于车辆i，其干扰信号是等效信道增益小于它的那些车辆的信号集合。我们假设N辆车辆按照其信道增益的降序共享同一信道： γ 0 1 γ 0 2 · · · γ 0 N。然后可以计算车辆n的干扰信号：

$$
I_n= \sum_{i=n+1}^{N} p_{i,0}(\gamma_0^i)^2 . (5)
$$

我们可以得到车辆i与基站之间的数据传输速率如下：

$$
υ_{i,0}(t)= b_{i,0}(t) \log_2 \left(1+ \frac{p_{i,0}(t)(\Gamma_k^i(t))^2}{\sigma^2 + I_i}\right). (6)
$$

最后，车辆i的通信速率可以表示为：

$$
R_{comm}^{i, k} (t)= a_{i, k}(t)υ_{i, k}(t),\forall i \in U, k \in K. (7)
$$

总计所有接入路侧单元k的车辆的总通信速率不得超过其容量，即 e.,

$$
\sum_{i\in U} R_{comm}^{i, k} (t) Z_k,\forall k \in K. (8)
$$

同样，一个区域内车辆的总通信速率不能超过总容量，因此应满足以下约束条件：

$$
\sum_{i\in U} R_{comm}^{i, k} (t) Z. (9)
$$

3.2 计算模型

在本文中，我们主要关注那些可以将卸载任务划分为多个部分并在不同平台上处理的应用程序，例如在线游戏、增强现实和自然语言处理。我们将车辆i的上传计算任务定义为ξ i={ di, ci}，其中di是计算任务的数据大小，ci是完成该任务所需的CPU周期数。随后，路侧单元或基站将计算结果发送回车辆i。由于MEC服务器位于路侧单元附近，它们之间的传输时间可以忽略不计[26]。此外，任务卸载的输出数据大小通常远小于输入数据大小，因此回程链路（即下行链路）的传输延迟也被忽略[2]。

我们定义分配给车辆i的RSU和基站k的计算能力（即每秒CPU周期）为fi, k。我们假设RSU以抢占式方式工作，这意味着它们按顺序处理车辆的通信请求（即 ∑i∈U ai, k 1,∀k ∈ K）。尽管如此，当多辆车辆在同一个RSU的无线覆盖范围内移动时，它们可能共享一个MEC服务器。由于MEC服务器的资源约束，无法保证所有车辆都能获得完整且充足的计算能力。因此，fi, k可以被建模为一个随机变量，并划分为N个级别： ε={ε0, ε1,…， εN −1}，其中N表示可用的计算能力状态数量。令Fi, k(t)表示在时隙t的瞬时计算能力。类似于信道增益γ k i，我们将fi, k建模为有限状态马尔可夫信道（FSMC）。瞬时计算能力Fi, k(t)的计算能力转移概率矩阵如下所示：

$$
\Theta_{i, k}(t)=[\theta_{x_s , y_s}(t)]_{N×N}, (10)
$$

其中 θx s ,ys(t) =Pr (Fi, k(t+ 1) = ys | Fi, k(t) = xs)，且 xs,ys ∈ ε。

路侧单元k上计算任务 ξ i的任务执行时间可通过以下公式计算： Δi, k= ci/f i, k。因此，可得到计算速率（即比特每秒）：

$$
r_{comp}^{i, k} = \frac{d_i}{\Delta_{i, k}} = \frac{f_{i, k}d_i}{c_i}. (11)
$$

路侧单元k在时隙t对车辆i的瞬时计算速率为：

$$
R_{comp}^{i, k}(t)= a_{i, k}(t)r_{comp}^{i, k}(t)= a_{i, k}(t) \frac{F_{i, k}(t)d_i}{c_i}, (12)
$$

其中，在MEC服务器上的并发计算的数据大小不能超过其计算容量。因此，应满足以下约束条件：

$$
\sum_{i\in U} a_{i, k}(t)d_i D_k ,\forall k \in K, (13)
$$

其中D k de表示MEC服务器上可同时处理的最大数据大小。

4 问题建模

本节中我们对优化问题进行建模。由于一段时间内的匹配问题是NP难问题，因此将原问题分解为两个子优化问题。

4.1 优化目标

当一辆移动车辆生成一个卸载任务时，它会检测周围可用的路侧单元和基站，并记录任务相关信息以及可用的计算资源信息。然后，它通过长期演进技术将该事件发送到附近的基站。基站接收到该事件的详细信息后，将立即执行资源分配，并通过某一区域内的路侧单元广播所获得的调度方案。传统的基站负责所有任务的执行，这可能导致较大的通信延迟和过高的能耗。这不仅无法保证用户的体验质量，也使得网络运营商的利润非常低。为了在保证网络运营商（即本文中的路侧单元和基站）收益的同时最大化车辆的用户体验质量，构建了一个协作式卸载网络系统。车辆在时隙t的瞬时用户体验质量可通过以下方式获得：

$$
R_{i, k}(t)= R_{comm}^{i, k}(t)+ R_{comp}^{i, k}(t). (14)
$$

我们系统中的流量调度与资源分配（TSRA）联合优化问题表述如下：

$$
\max_{a_{i, k}(t)} R=\sum_{i\in U} \sum_{k \in K} M_{i, k} \sum_{t=1}^{T} R_{i, k}(t), (15)
$$

s.t.={ ai, k(t) ∈{0, 1},∀i ∈ U, k ∈ K, Equations(1),(8),(9),(13).

由于所构建的TSRA问题受到多种因素的约束，耦合变量使得该优化问题难以求解。为解决此问题，并在用户服务质量体验与网络运营商收益之间进行权衡，我们将原始的 TSRA问题分解为两个子优化问题。在第一阶段，通过设计效用函数来确定多辆车辆的优先级。随后，利用改进的深度Q网络（DQN）算法获得调度结果，并将每个用户映射到相应的路侧单元或基站。

4.2 卸载任务调度

多辆车辆在同一时隙选择同一个路侧单元的情况很常见，这会导致约束条件（1）无法满足。因此，第一个子优化问题将用户服务质量体验纳入考虑，旨在找到一个合理的、彼此之间不冲突的所有车辆调度列表。

我们将灵活的效用函数定义为用户满意度水平。效用函数的值取决于任务、通信信道状态以及车辆与路侧单元之间的距离。该效用函数包含四个参数：优先级、紧急程度、信道增益和距离。信道增益 γ k i 在第三节-C中已介绍，用于反映通信信道状态。距离 di, k 表示车辆与路侧单元或基站之间的欧氏距离。优先级 π(p)设定了效用函数的上界，其中优先级p ∈{critical, high, medium, low }。如果车辆的任务卸载请求被立即响应，则其效用函数取对应任务优先级的上界值，记为 π(p)；否则，其效用函数的值将随时间推移而下降。

紧急程度 ρ(r)用于建模车辆效用函数随响应延迟增加而发生的指数衰减率，其中紧急程度 r ∈{extreme, high, medium, low }。任务的紧急程度越高，随着延迟的增加，效用函数下降得越快。当任务优先级固定时，不同紧急程度下效用函数的值如参考文献[12]所示。

如参考文献[29],所述，将S形行为纳入车辆资源分配的效用函数至关重要。我们采用类S形函数来建模车辆 i ∈ U的效用，其参数包括优先级 π(i)(p)、紧急程度 ρ(i)(r)、信道增益 γ k i以及距离 di, k，具体如下：

$$
Y_{i, k}= \frac{\pi(i)(p)}{d_{i, k}+ \exp(-\rho(i)(r)(\gamma_k^i - b_{i, k}))} , (16)
$$

其中，常数参数 bi, k 用于微调效用函数。参数 π(i)(p) 类似于传统的权重因子，而 ρ(i)(r) 控制 Yi, k 的陡峭程度。 ρ(i)(r) 越大，Yi, k 随 γ k i 的增加速度越快。

我们的目标是最大化车辆效用的平均值。优化函数如下：

$$
\max \frac{1}{|U|}\sum_{i\in U} a_{i, k}Y_{i, k}, (17)
$$

s.t.=
$$
\begin{cases}
p \in{critical, hiдh, medium, low}, \
r \in{extreme, hiдh, medium, low}, \
0< d_{i, k} \Delta, \
a_{i, k} \in{0, 1},\forall i \in U, \
\sum_{i\in U} a_{i, k}(t)= 1,\forall k \in K, \
Equation(1),
\end{cases}
$$

其中 Δ表示RSU无线覆盖半径。当车辆独立选择不同的路侧单元时，会产生不同的效用值，车辆力求最大化自身的效用以确保其用户体验质量。由于一个路侧单元在同一时间只能被一辆车辆接入的限制，卸载决策之间可能会产生冲突。

4.3 基于强化学习的任务卸载

在本小节中，我们将资源分配优化问题建模为一个DRL过程。在通过求解任务调度问题获得车辆服务队列后，我们的目标是通过确定车辆的卸载决策来最大化车辆整体QoE。由于变量、庞大的环境状态空间和系统动作随时间动态变化，使用传统优化方法几乎无法解决这一复杂问题。因此，我们利用近期提出的渐进式DQN来有效且高效地生成针对车辆的系统动作。

为了减少往返时间，车辆选择基站作为DQN代理，负责与环境交互并做出决策。我们假设MEC服务器的计算状态实时更新，并在路侧单元之间共享。该代理从MEC服务器和车辆收集状态信息。如前所述，车辆移动性通过广播实时获取。随后，代理通过构建系统状态并选择最优动作来做出卸载决策。最后，所有最优动作可广播给车辆。

接下来，我们确定DQN模型中的系统状态、动作和奖励函数：

(1) 系统状态 通信信道增益和可用计算能力的状态由信道增益 γ k i 和计算能力fi, k的实现决定。

因此，复合状态 χi(t) ∈R2×K 可表示如下：

$$
\chi_i(t)= [\Gamma_1^i(t), \Gamma_2^i(t),…, \Gamma_i^K(t), F_{i,1}(t), F_{i,2}(t),…, F_{i,K}(t)]. (18)
$$

(2) 系统动作 在深度Q网络中，智能体负责选择路侧单元或基站来处理车辆 的任务卸载。卸载分配定义为一个二进制变量向量 i<,> k( )，其表示如下：

$$
a_i(t)=[a_{i,1}(t), a_{i,2}(t),…, a_{i,K}(t)]. (19)
$$

(3) 奖励函数 我们的目标是最大化车辆的综合用户体验质量（QoE），包括频谱带宽和计算资源的租赁成本。因此，将QoE Ri(t) 设定为系统的奖励。此外，网络运营商对车辆的任务执行和虚拟网络接入进行收费，其单价分别为 ϕ i每Mbps和 τi每Mbps。然而，运营商需要支付带宽租赁费用，定义为 δk每赫兹用于路侧单元k。同时，任务执行的能耗也需考虑在内。路侧单元k的计算单位成本表示为 ηk每焦耳。为了统一标准，定义 ςk为路侧单元k运行一个中央处理器周期的能耗，其单位为瓦特每赫兹。另外，由路侧单元处理的卸载任务比例用ϱ i表示。我们假设卸载任务可以被划分为多个部分，并分别由MEC服务器和基站处理。当车辆在完成卸载任务前驶出路侧单元的通信范围时，基站可以继续处理剩余的任务。最后，我们定义车辆i的奖励函数为：

$$
R_i(t)=\sum_{k \in K} R_{comm}^{i, k}(t)+\sum_{k \in K} R_{comp}^{i, k}(t)
= \sum_{k=1}^{K} (\tau_i R_{comm}^{i, k} -\delta_k b_{i, k}(t))+(\tau_i R_{comm}^{i,0} -\delta_k b_{i,0}(t))
+ \sum_{k=1}^{K} (\varrho_i \phi_i R_{comp}^{i, k} -\eta_k c_{i, k} \varsigma_k)+((1 - \varrho_i)\phi_i R_{comp}^{i,0} -\eta_0 c_{i,0} \varsigma_0)
= \sum_{k=1}^{K} \left(\tau_i b_{i, k}(t) \log_2\left(1 + \frac{p_{i, k}(t)(\Gamma_k^i(t))^2}{\sigma^2}\right) -\delta_k b_{i, k}(t)\right) +\left(\tau_i b_{i,0}(t) \log_2\left( 1+ \frac{p_{i,0}(t)(\Gamma_k^i(t))^2}{\sigma^2+ I_i}\right) -\delta_k b_{i, k}(t)\right)
+ \sum_{k=1}^{K} a_{i, k}(t)\varrho_i\left(\phi_i \frac{F_{i, k}(t)d_i}{c_i} -\eta_k c_{i, k} \varsigma_k\right)+ a_{i,0}(t)(1 - \varrho_i)\left(\phi_i \frac{F_{i,0}(t)d_i}{c_i} -\eta_0 c_{i,0} \varsigma_0\right).
(20)
$$

智能体可以通过在时隙t执行所选择的动作ai, k(t)，获得即时奖励Ri(t)。深度Q网络的目标是通过获取最优策略来最大化累积奖励。因此，该优化问题可表述如下：

$$
R_i = \max_{a_{i, k}(t)} \sum_{t=0}^{T-1} \epsilon^t R_{i, k}(t), (21)
$$

s.t.=
$$
\begin{cases}
a_{i, k} \in{0, 1},\forall k \in K, \
0 \varrho_i 1,\forall i \in U, \
Equation(8),(9),(13),
\end{cases}
$$

其中参数 ϵ是每个时隙中用户体验质量的权重， ϵ ∈(0, 1]。

5 车载网络中的集成深度强化学习

在求解所提出问题之前，本节简要介绍车载网络中强化学习和集成DQN的概述。

5.1 车载网络中的强化学习

强化学习包含四个关键要素：智能体、环境状态、奖励和动作。在每个回合中，智能体根据当前环境状态选择一个动作，并在执行所选动作后获得奖励。环境状态通常被建模为马尔可夫决策过程（MDP）。因此，强化学习问题可以表述为MDP中的最优控制问题。环境状态空间和动作空间是有限且明确的。利用强化学习的目的是智能体在与环境交互时通过采取一系列动作为最大化总奖励[39]。由于车辆的计算和缓存能力有限，在每辆车内部署计算密集型的深度神经网络应用是不合理的。因此，在我们的模型中，基站（BS）充当智能体的角色，旨在通过提供网络服务来获取利润（即奖励）。时变参数信道状态γ k i和计算能力 fi, k是环境状态。动作空间是可用的卸载服务器。基站选择动作为车辆进行调度以实现利润最大化。这可以被视为一个典型的强化学习问题。

与传统机器学习方法（如监督学习）不同，即使有经验丰富的指导者提供带标签的历史数据，强化学习也无法从中学习。试错搜索和延迟奖励是强化学习的两个显著特征[11]。前者是为了在探索与利用之间进行权衡；后者使智能体能够考虑车辆的累积奖励。通常，强化学习算法包括Q学习、SARSA和深度Q网络。

5.2 集成DQN

传统深度强化学习在实际应用中存在许多缺点，例如收敛速度慢和过高估计。我们采用两种方法来改进深度Q网络算法。

5.2.1 Dropout正则化

正则化减少了网络参数的数量，并将深层复杂神经网络转换为线性简单网络，以降低DQN的方差。此后，参数矩阵变为稀疏矩阵。在我们的模型中，Dropout正则化通过随机失活部分神经元并将其权重设置为零，从而降低参数矩阵 θ的复杂性。由于每一层中的神经元都是随机丢弃的，训练后的神经网络比正常网络小得多，因此可以避免过拟合问题。此外，整个网络不会偏向某些特征（例如，特征的权重值非常大），因为在Dropout正则化中每个特征都可能被丢弃。因此，每个特征的权重可以赋予较小的值，这类似于L2正则化（||θ ||22 =∑ #neurons j =1 θ2 j = θ
Tθ）。Dropout正则化中最关键的参数是失活概率。例如，如果我们把失活概率设为0.2，则有20%的神经元可以被失活。随机失活会降低期望结果值。当我们在隐藏层上执行Dropout正则化时，其输出的期望值会因失活概率而降低，从而影响未来预测。因此，我们将结果除以失活概率，以保持其期望值不变。具体实现如下：

keep.prob= 0.8; d3= np.random.rand(a3.shape[0], a3.shape[1])< keep.prob; a3= np.multiply(a3, d3); a3= a3/keep.prob; z4= np.dot(w4, a3)+ b4.
(22)

5.2.2 双重DQN（DDQN）

基于Q学习的框架，深度Q网络使用卷积神经网络来表示动作‐价值函数。然而，深度Q网络无法克服Q学习固有的缺点，即过高估计。为了解决这个问题，Hasselt [25]提出了双重DQN，通过使用不同的价值函数来评估动作的选择和动作的评估。我们从价值函数的公式化表达方面比较Q学习、深度Q网络和双重DQN之间的差异如下：

$$
Y_t^Q= R_t+ \gamma \max_a Q(S_{t+1}, a;\theta_t), \
Y_t^{DQN} = R_t+ \gamma \max_{a’} Q(S_{t+1}, a’;\theta_{t-}), \
Y_t^{DDQN} = R_t+ \gamma Q(S_{t+1}, \arg\max Q(S_{t+1}, a;\theta_t);\theta_{t-}).
(23)
$$

在Q学习和深度Q网络中，它们的动作选择策略都是贪婪的。然而，双重DQN使用神经网络来评估选择策略，并逼近真实价值函数。

6 基于深度强化学习的智能卸载系统

我们在第3节中提出了TSRA问题，并将其分解为两个子优化问题。在本节中，我们阐述了智能卸载系统，该系统包含两个模块。第一个是多辆车辆之间的任务调度，为此提出了一种双边匹配算法来解决该问题。第二个是资源分配，我们采用集成的深度强化学习方法来解决该问题。

6.1 系统概述

整个任务卸载过程如图2所示。第一步，所有车辆广播其位置信息并更新其可用RSU列表。之后，车辆计算效用值并构建相应的偏好列表。然后，它们向基站发送卸载请求。在第三步中，基站执行任务调度和资源分配，并将任务分配发送给路侧单元。最后，所有车辆将其卸载任务发送到相应的路侧单元。表1总结了本文中主要使用的系统变量。我们智能任务卸载系统的伪代码如算法1所示。

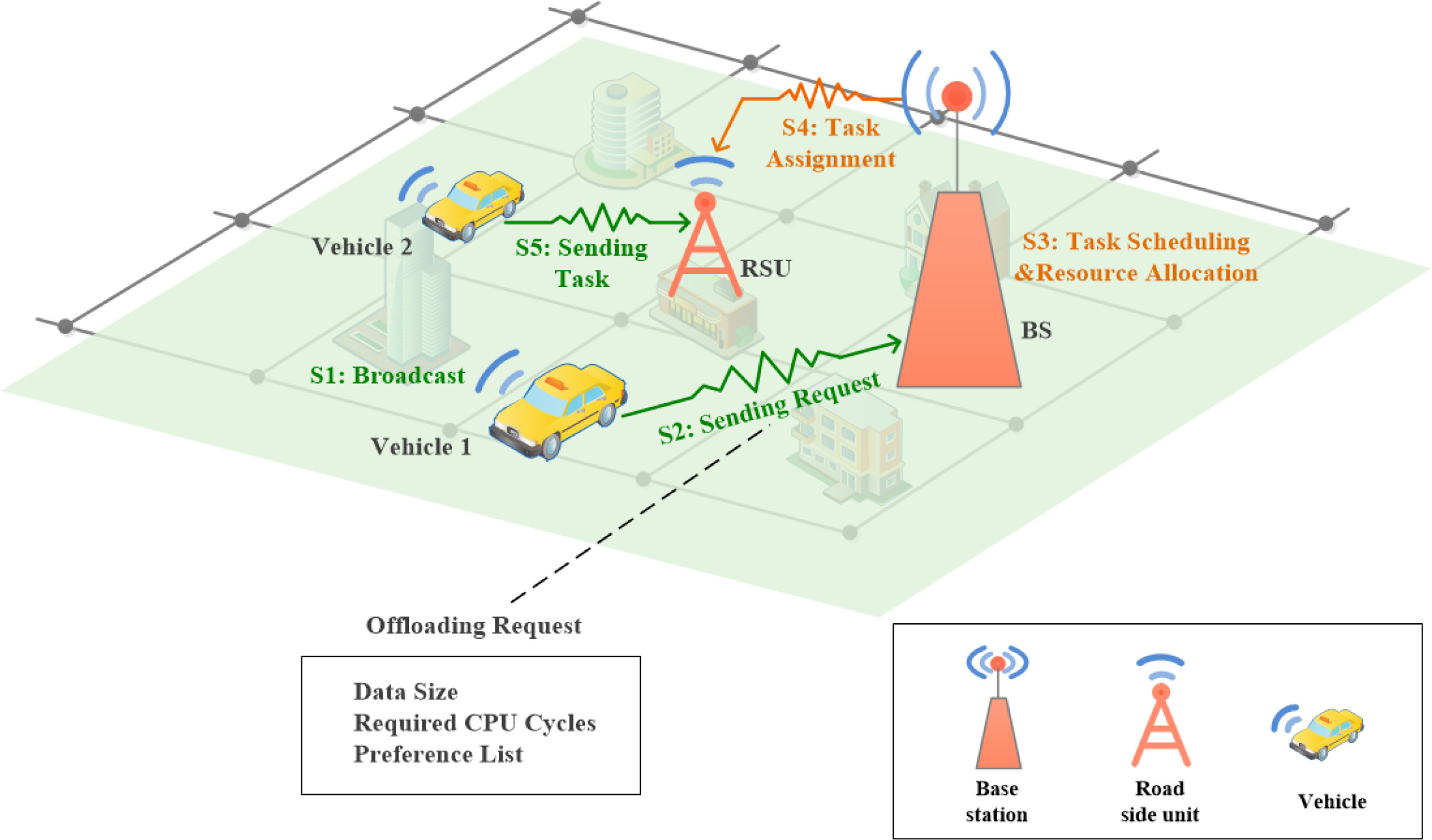
表1. 系统变量

变量	描述
Vi	车辆 i
k	路侧单元 k
qv	一辆车辆可同时访问的路侧单元数量
qR	一个路侧单元可同时服务的车辆数量
Pi	车辆i的偏好列表
Yi, k	车辆 在路侧单元 服务下的效用值
Ak	路侧单元k的接受集合
Fk	路侧单元k的禁止列表
θ	评估深度Q网络的权重
θ⁻	目标深度Q网络的权重

算法1: 智能卸载系统的伪代码。

车辆广播其位置信息；
车辆向基站发送卸载请求；
任务调度 = 算法3;
对于任务调度中的每辆车i 执行
    算法4;
end
基站向路侧单元发送任务分配；
路侧单元执行任务卸载；

6.2 任务调度的双边匹配

为解决任务卸载请求调度过程中出现的冲突，将调度过程建模为双边匹配模型，并设计了动态车联式匹配算法（DVIM）以寻找最优匹配。我们假设一辆车辆最多可同时接入qv个路侧单元。一个路侧单元在同一时间最多可服务qR辆车辆。此外，每个路侧单元维护两个列表：禁止列表 Fk 和接受集合 Ak。传统的静态匹配算法每次都需要遍历完整的集合，耗时且浪费计算资源。为了降低所设计算法的计算复杂度，被路侧单元k拒绝的用户将被加入禁止列表，默认情况下，它们在本轮中无法再次被选择。类似地，接受集合用于记录路侧单元k当前已接受的任务卸载请求。

我们现在详细阐述DVIM算法的整个过程。该算法首先初始化禁止列表和接受集合。接着，每辆车辆计算将其任务卸载到路侧单元k时所获得的效用Yi, k，然后所有车辆根据Yi, k的降序构建各自的偏好列表 Pi。在匹配迭代阶段，每个已匹配的路侧单元数量少于qv的车辆，会向其偏好列表 Pi中最优先的路侧单元发送卸载请求，并将该路侧单元从自身的偏好列表中移除。当所有车辆发出请求后，收到请求的路侧单元将决定是否接受这些请求。通常，路侧单元会接受那些能够提高整体效用值的请求。如果路侧单元k已经与qR辆车辆匹配，则它将与最不重要的车辆解除匹配。然后，所有响应将被发送回车辆。当车辆的匹配路侧单元数量少于qv个且其偏好列表非空时，车辆将继续发送卸载请求。当不再有车辆愿意发送卸载请求时，该算法终止。

算法2：基于效用选择算法的伪代码。

对于 每辆车i = 1, 2, ..., U do
    如果 vehiclei-matched-number < qv 且 Pi ≠ ∅，那么
        车辆 i 向 Pi[1] 提出自身请求；
        车辆-提出 = 1
        从 Pi 中移除 Pi[1]
    end
end
对于 每个路侧单元 k = 1, 2, ..., K do
    如果 路侧单元k已收到任何请求，记为Vi 则
        如果 Yk(({Vi} ∪ Ak)) > Yk((Ak)) 则
            路侧单元 k 接受来自Vi的请求；
            如果 || Ak || ≥ qR，则
                对于每辆车i ∈ Ak 执行
                    计算 Yk((Ak \ Vi))；
                end
                在上述循环中找到最大的效用函数，记为 Yk((Ak \ Vn))；
                与路侧单元k不匹配的对向车辆Vn；
                将车辆 n 添加到 Fk
            end
        else
            拒绝来自Vm的请求；
            将车辆 m 添加到 Fk 中
        end
    end
end

6.3 基于深度强化学习的移动感知任务卸载

第二个子优化问题是基于马尔可夫链的资源分配与卸载决策的联合优化问题。当考虑一系列时隙中的环境状态时，该问题变得复杂。因此，设计了一种改进的深度强化学习方法。

首先，初始化经验回放内存D，其可存储N个转移。动作‐价值函数Q通过随机权重 θ进行初始化，用于计算时间差分（TD）目标的目标Q网络也以相同的权重初始化，即 θ⁻ = θ。接着，在任务中调度卸载请求。对于每个事件中的每一步，以概率 ε从可用接入列表中随机选择一个路侧单元。否则，采用贪婪策略选择当前动作‐价值函数中 Q‐值最大的路侧单元。当选定路侧单元k后，观察即时奖励rt以及下一状态。因此，可以获得一组转移（observation，action，reward，next observation）并将其存储在回放缓冲区中。在神经网络学习阶段，深度Q网络随机采样一个小批量转移从回放缓冲区D中抽取每个样本时，需判断下一个状态是否为事件的终止状态。若是，则 TD目标为rj；否则，使用目标DQN计算TD目标：yj=rj+ γQ(xj+1, arg maxa′ Q(xj+1, a′; θ); θ⁻)。接着，以最小化方差误差为目标进行梯度下降，更新评估Q网络的参数：Δθ= α[r + γmaxa′ Q(s′, a′; θ⁻) − Q(s, a; θ)]∇Q(s, a; θ)。最后，每C步更新一次TD目标网络参数和随机概率 ε，从而确保目标Q网络能够较好地拟合动作‐价值函数，并加快收敛速度。

上述过程如算法4所示。

算法3：DVIM算法的伪代码。

初始化禁止列表 Fk 为空；
将接受集合 Ak 初始化为空；
for 每辆车i = 1, 2, ..., U do
    对于每个路侧单元 k = 1, 2, ..., K do
        如果 车辆i ∉ Fk 那么
            计算效用函数值 Yk(Vi);
        end
    end
end
车辆 i 构建偏好列表 Pi；
匹配迭代 = 1；
车辆-提出 = 0;
while 匹配迭代 == 1 或 车辆-提议 == 1 do
    匹配迭代 += 1；
    算法2
end

算法4：基于移动性感知的DDQN伪代码。

输入：系统状态 χi(t)，可用的动作空间 K；
输出：最大用户体验质量 Ri

初始化容量为N的回放缓冲区D；
使用权重 θ 初始化评估深度Q网络；
使用权重 θ⁻ = θ 初始化目标深度Q网络；

对于 每个回合 i = 1, 2, ..., U 执行
    初始化观测值s1，并预处理序列 x1 = φ(s1)；
    for t = 1, 2, ..., T − 1 do
        以概率 ε 选择一个随机动作 ai,k(t);
        否则，选择 at = argmaxai,k(t) Q(x, a; θ);
        执行动作 ai,k(t);
        观察即时奖励 rt = Ri(t) 和下一个观测状态 st+1。
        将过程 st+1 作为下一个状态 xt+1 = φ(st+1)。
        将转移 (xt, at, rt, xt+1) 存入 D；
        从D中采样随机小批量的转移(xj, ai, rj, xj+1)；
        if 回合 在步骤 j 终止 + 1 then
            目标 Q‐值 yj = rj
        else
            yj = rj + γQ(xj+1, arg maxa′ Q((xj+1, a′;θ));θ⁻);
        end
        对(yj − Q((xj, aj; θ)))² 执行梯度下降；
        每C步，以速率 σ 和 μ 更新目标深度Q网络参数和概率 ε；
        θ⁻ = σθ + (1 − σ)θ⁻, ε = ε − με.
    end
end

7 性能评估

在本节中，我们对所提出的算法DVIM和移动性感知双DQN（MADD）的性能进行了评估。对于第一个模块，我们将DVIM算法与穷举搜索、贪心算法和随机排序方法进行了比较。仿真结果表明，DVIM在网络性能和执行时间之间实现了良好的权衡。对于第二个模块，MADD相较于传统DQN、Q学习以及两种基线算法表现出更优的性能。

7.1 仿真设置

在实现DVIM算法之前，需明确函数（公式(17)）中的参数。参考文献[12]提供了一个联合概率分布，其中大多数卸载任务具有中等或低优先级和紧急程度。通常，重要任务（如交通拥堵甚至交通事故）具有关键或高优先级以及极端或高紧急程度。因此，我们将不同级别任务的比例设置为3][12]。优先级定义了卸载任务能够达到的最大效用值，由 π(i)(关键) = 8、π(i)(高) = 4、π(i)(中等) = 8、π(i)(低) = 1设定。紧急程度决定了效用函数的指数衰减率，由 ρ(i)(极端) = 0.6、ρ(i)(高) = 0.2、ρ(i)(中等) = 0.1、ρ(i)(低) = 0.01[12]设定。此外，我们考虑在基站通信范围内存在五个路侧单元和一些具有计算卸载请求的车辆。性能指标如下：

（1）总效用：DVIM算法的优化目标是最大化所有车辆的总效用，以衡量用户的用户体验质量。（2）执行时间：算法获取任务调度结果所消耗的时间。（3）平均用户体验质量：网络运营商从车辆获得的平均利润。

对于第二模块，关键参数在表2中列出。转移概率矩阵设置如下[11]：

$$
\Theta=
\begin{bmatrix}
0.5 & 0.25 & 0.125 & 0.0625 & 0.0625 \
0.0625 & 0.5 & 0.25 & 0.125 & 0.0625 \
0.0625 & 0.0625 & 0.5 & 0.25 & 0.125 \
0.125 & 0.0625 & 0.0625 & 0.5 & 0.25 \
0.25 & 0.125 & 0.0625 & 0.0625 & 0.5 \
\end{bmatrix}
$$

对于通信状态，我们设置转移概率 γki = 0.7，且ψдs, hs(t) = 0.3。为了实现基于DDQN的MADD算法，在Ubuntu 16.04 LTS上使用Python Anaconda 4.3和TensorFlow 0.12.1。将四种方案与MADD算法进行比较：

（1）DQN：传统DQN方法使用一个价值函数来评估动作的选择。通常，DQN方法倾向于选择使下一步奖励值最大的动作，从而不可避免地导致过高估计。（2）Q学习：作为一种经典的时序差分算法，它总是选择下一时刻最大的动作值作为目标。此外，还需要记录所有状态‐动作对的奖励。（3）贪心算法：与强化学习相反，贪心算法选择当前时刻奖励值最大的动作。（4）本地计算：它是一种基线算法，其中所有车辆都将任务卸载到本地基站。

7.2 仿真结果

本小节阐述了智能卸载系统的性能评估，包括任务调度和资源分配两个模块。

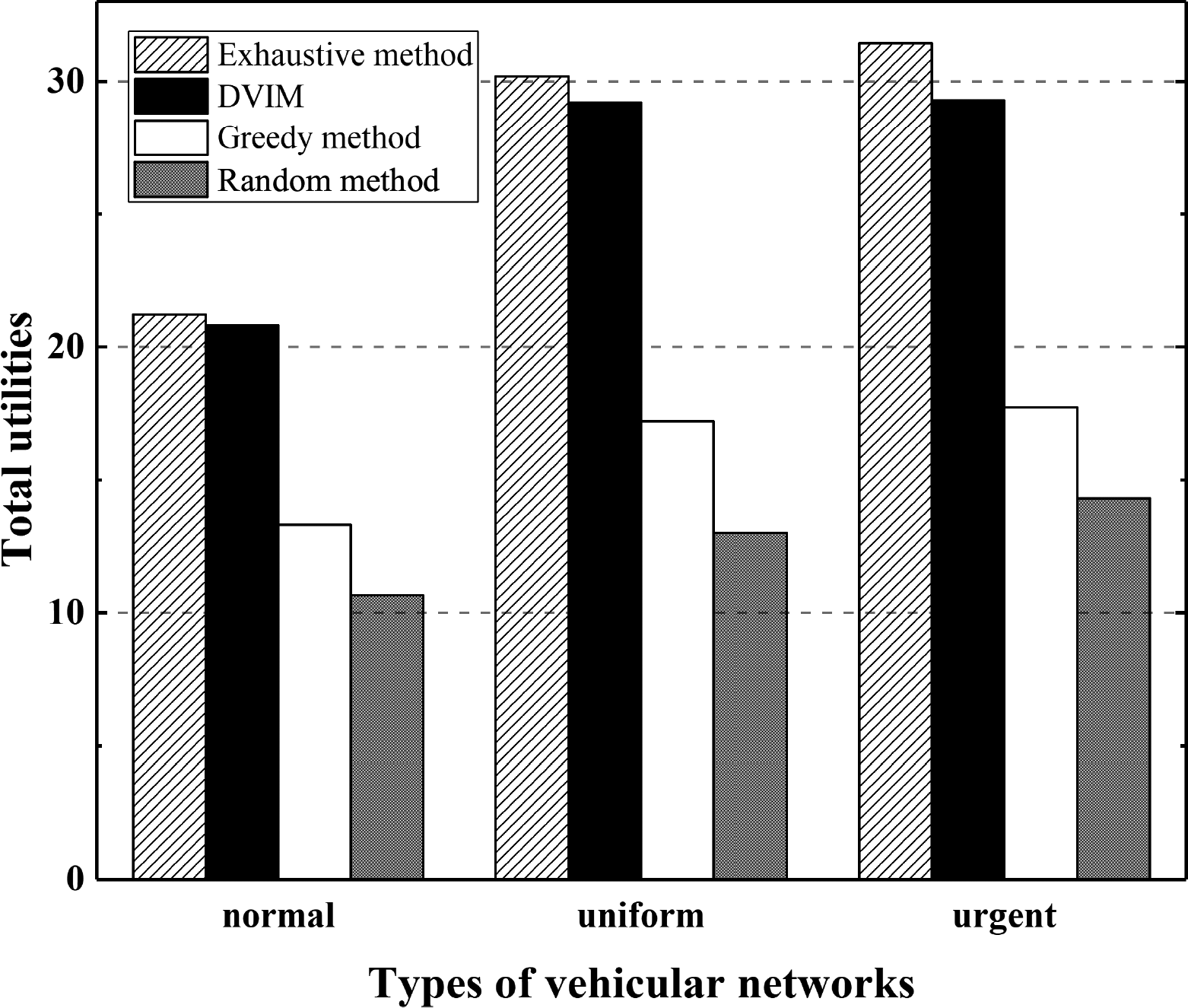
图3展示了在不同车辆数量下总效用的对比。当车辆数量较小时，DVIM算法几乎可以表现得与穷举算法。由于任务卸载的随机性，总效用随着车辆数量的增加呈非线性增长。当车辆数量较大（例如 U= 9）时，DVIM算法仍保持良好的性能，仅比穷举算法低5%。由于资源竞争加剧，贪心算法性能下降。DVIM的总效用比贪婪方法高出22%。综上所述，我们提出的DVIM算法性能接近穷举算法，在车辆数量较多、即资源竞争激烈的情况下，优于贪心算法和随机算法。

图4展示了不同类型车载网络中总效用的比较。在普通车载网络中，四级卸载任务（关键或极端、高、中等和低）的比例为[0.1,0.2,0.4,0.3]。根据参考文献[12],，可以合理假设70%的任务具有中等或低的优先级和紧急程度。穷举算法的结果可视为上界。所提出的DVIM算法能够达到上界性能的98%，比贪心算法高出20%，比随机算法高出近50%。在局部区域或特定时间段内（例如早晚交通高峰期），各层级任务的比例会随车载网络状态而变化。与交通拥堵或事故相关的高优先级和紧急任务被频繁上传。因此，我们还在均匀车载网络和紧急车载网络中评估了DVIM算法的性能，其中任务比例分别为[0.25,0.25,0.25,0.25]和[0.4,0.4,0.1,0.1],。在均匀车载网络中，DVIM的性能比穷举搜索低3.4%，但比贪婪方法高出41%。在紧急车载网络中，DVIM能达到上界性能的93%，相比贪婪方法提升65%。普通环境下的卸载任务的优先级和紧急程度低于均匀和紧急环境中的对应值，因此其可实现的效用上界也低于另外两种情况。综上所述，在兼顾个人优先级和总体效用的情况下，DVIM算法的性能可接近通过穷举算法获得的上界，平均比贪心算法高出40%。

不同算法的执行时间在图5中进行了比较。当有五辆车辆时，所提出的DVIM、贪婪方法和随机方法之间的执行时间差异非常接近。穷举搜索的执行时间比其他三种算法高10倍。此外，DVIM、贪婪方法和随机方法的执行时间随车辆数量增加而缓慢增长，而穷举法的执行时间则呈指数级增长，因为搜索空间急剧增加。当车辆数量为10时，穷举搜索的执行时间比其他三种算法高出500倍。尽管穷举法能够达到上界，但由于其高时间复杂度，实际应用中并不可行。此外，实验表明，我们提出的DVIM算法能够在时间消耗显著降低的情况下，逼近穷举算法的性能。

图6显示了卸载数据大小 di从10MB到60MB变化的影响。整体平均用户体验质量随着数据大小的增加而稳步增长。本地计算（即所有计算任务均由基站完成）的增长速度在各方案中是最慢的。这是因为基站传输和处理大量数据时消耗的资源和能量比路侧单元更多。随着对近程和优先服务需求的不断增长，路侧单元更适合处理大量数据。由于DQN方法无法克服过高估计的缺点，我们提出的MADD算法性能平均比DQN方法高出15%。Q学习和贪婪方法未充分考虑网络状态的动态变化，其性能分别比MADD算法低25%和35%算法。综上所述，所提出的MADD算法性能优于其他现有方案。当卸载数据量增加时，其性能优势也随之增加。

如图7所示，我们评估了车辆在虚拟网络接入的单位计费价格τi变化时的平均用户体验质量k。我们注意到，当接入费用从10增加到20时，MADD获得的整体用户体验质量仅增加了6.5%；当接入费用从50增加到60时，仅增加了5.2%。因此，网络运营商通过无限制提高接入费用来获取更多利润是不合理的。当单位计费价格较高时，价格上涨可能会促使用户选择基站。

的影响 ϕk，即RSU k的任务执行单位收费价格，在图8中显示。当 ϕk上升时，基于MEC的卸载的接入量普遍增加。因此，平均用户体验质量随着任务执行单位收费价格的上升而线性增加。由于本地计算不占用MEC服务器，平均用户体验质量保持不变。所提出的MADD算法的性能分别比DQN方法和贪婪方法高出约12%和20%。这是因为目标网络是独立构建的，且通过应用双重DQN框架解决了过高估计问题。总体而言，MADD算法在本地车载网络中表现良好。

8 结论

在本文中，我们专注于车载边缘计算的深度强化学习，并构建了一个智能卸载系统。网络状态被建模为有限状态马尔可夫链。同时考虑了车辆移动性和非正交多址接入。该卸载系统包含两个模块，即任务调度模块和资源分配模块。针对这两个模块的联合优化问题被建模，目标是最大化车辆的总体用户体验质量。由于所建模问题具有NP难特性，因此将其分解为两个子优化问题。对于第一个子问题，设计了一种双边匹配方法来调度卸载请求，以最大化车辆的效用。对于第二个子问题，开发了一种基于DDQN的算法进行求解。数值结果表明，在不同的网络场景下，第一模块中的匹配算法能够达到穷举算法95%的性能，同时执行时间减少超过90%。对于第二模块，基于DDQN的算法比传统DQN方法性能提升10%至15%。因此，我们的卸载系统高效且有效。在未来的工作中，我们将研究如何实现具有良好安全性的节能型车载边缘计算[32, 33]。