1. 多相分解的概念
多相分解技术在多速率信号处理中有着重要的作用。使用多相分解技术可以在信号速率转换过程中去掉不必要的计算,从而大大提高运算的速度。多相分解技术可以应用在整数倍抽取、整数倍内插,以及分数倍速率转换系统中。
对于一个抽取倍数为M的系统,假设抽取前的FIR滤波器长度为N,则滤波器的输入/输出关系为
v
(
n
)
=
∑
m
=
0
N
−
1
h
(
m
)
x
(
n
−
m
)
v(n)=\sum_{m=0}^{N-1}h(m)x(n-m)
v(n)=m=0∑N−1h(m)x(n−m)
滤波后,需要对数据
v
(
n
)
v(n)
v(n)每M个点进行一次抽样,作为抽取系统的输出。因此,在上式中只需要在
n
=
k
M
(
k
=
1
,
2
,
⋯
)
n=kM(k=1,2,\cdots )
n=kM(k=1,2,⋯)时计算
v
(
n
)
v(n)
v(n)的值即可,可以跳过中间的其他计算。而采用FIR的一般结构却需要依次计算每个滤波器的输出。多相分解技术正式根据抽取及滤波器的特点,确保只计算需要抽取的样值,从而使整个滤波器的运算量减小到原来的1/M。
2. 整数倍抽取器的多相结构
考察一个抽取率为M的抽取系统,即
H
(
z
)
=
∑
n
=
0
∞
h
(
n
)
z
−
n
=
h
0
+
h
1
z
−
1
+
h
2
z
−
2
+
⋯
H(z)=\sum_{n=0}^{\infty }h(n)z^{-n}=h_{0}+h_{1}z^{-1}+h_{2}z^{-2}+\cdots
H(z)=n=0∑∞h(n)z−n=h0+h1z−1+h2z−2+⋯
=
h
0
+
h
M
z
−
M
+
h
2
M
z
−
2
M
+
⋯
+
h
1
z
−
1
+
h
M
+
1
z
−
(
M
+
1
)
+
h
2
M
+
1
z
−
(
2
M
+
1
)
+
⋯
+
⋯
+
h
M
−
1
z
−
(
M
−
1
)
+
h
2
M
−
1
z
−
(
2
M
−
1
)
+
h
3
M
−
1
z
−
(
3
M
−
1
)
+
⋯
=h_{0}+h_{M}z^{-M}+h_{2M}z^{-2M}+\cdots +h_{1}z^{-1}+h_{M+1}z^{-(M+1)}+h_{2M+1}z^{-(2M+1)}+\cdots +\cdots +h_{M-1}z^{-(M-1)}+h_{2M-1}z^{-(2M-1)}+h_{3M-1}z^{-(3M-1)}+\cdots
=h0+hMz−M+h2Mz−2M+⋯+h1z−1+hM+1z−(M+1)+h2M+1z−(2M+1)+⋯+⋯+hM−1z−(M−1)+h2M−1z−(2M−1)+h3M−1z−(3M−1)+⋯
=
z
0
(
h
0
+
h
M
z
−
M
+
h
2
M
z
−
2
M
+
⋯
)
+
z
−
1
(
h
1
+
h
M
+
1
z
−
M
+
h
2
M
+
1
z
−
2
M
+
⋯
)
+
⋯
+
z
−
(
M
−
1
)
(
h
M
−
1
+
h
2
M
−
1
z
−
M
+
h
3
M
−
1
z
−
2
M
+
⋯
)
=z^{0}(h_{0}+h_{M}z^{-M}+h_{2M}z^{-2M}+\cdots) +z^{-1}(h_{1}+h_{M+1}z^{-M}+h_{2M+1}z^{-2M}+\cdots) +\cdots +z^{-(M-1)}(h_{M-1}+h_{2M-1}z^{-M}+h_{3M-1}z^{-2M}+\cdots)
=z0(h0+hMz−M+h2Mz−2M+⋯)+z−1(h1+hM+1z−M+h2M+1z−2M+⋯)+⋯+z−(M−1)(hM−1+h2M−1z−M+h3M−1z−2M+⋯)
=
∑
l
=
0
M
−
1
z
−
l
∑
n
=
0
∞
h
(
M
n
+
l
)
z
−
M
n
=\sum_{l=0}^{M-1}z^{-l}\sum_{n=0}^{\infty }h(Mn+l)z^{-Mn}
=l=0∑M−1z−ln=0∑∞h(Mn+l)z−Mn
令
E
l
(
z
)
=
∑
n
=
0
∞
h
(
M
n
+
l
)
z
−
n
E_{l}(z)=\sum_{n=0}^{\infty }h(Mn+l)z^{-n}
El(z)=n=0∑∞h(Mn+l)z−n
则
H
(
z
)
=
∑
l
=
0
M
−
1
z
−
l
E
l
(
z
M
)
H(z)=\sum_{l=0}^{M-1}z^{-l}E_{l}(z^{M})
H(z)=l=0∑M−1z−lEl(zM)
式中,
h
(
M
n
+
l
)
h(Mn+l)
h(Mn+l)被称为多相分量。根据上式可得下图6-31所示的滤波器结构形式。再根据Nobel恒等式原来,将图中的抽取操作
↓
M
\downarrow M
↓M移入各支路,并与
E
l
(
z
M
)
E_{l}(z^{M})
El(zM)交换位置。
E
l
(
z
M
)
E_{l}(z^{M})
El(zM)移到
↓
M
\downarrow M
↓M右侧之后,
z
M
z^{M}
zM变为z,最终得到如图6-32所示的结构形式。为了区别变换前后的系统,变换后用
z
2
z_{2}
z2表示。
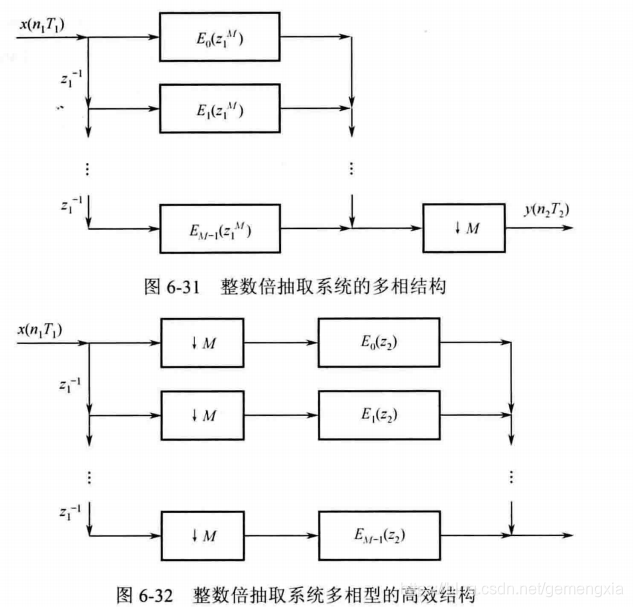
为了更清楚地看到多相结构抽取系统的全貌,设滤波器的阶数N=12,抽取因子M=3,并将
E
l
(
z
M
)
E_{l}(z^{M})
El(zM)的具体结构如图6-33所示。
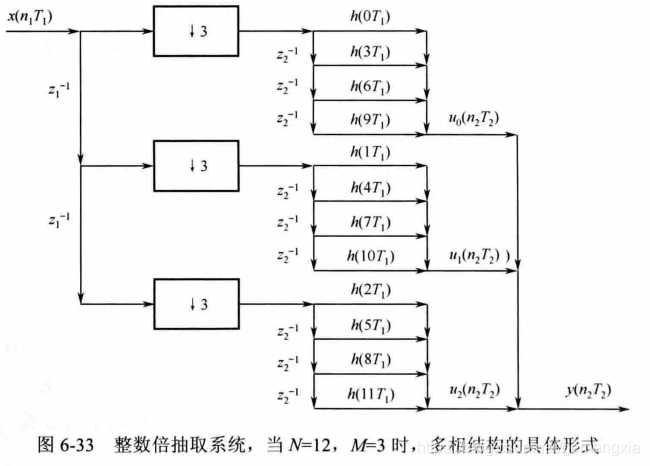
图中,
↓
M
\downarrow M
↓M右侧允许的运算时间
T
2
=
M
T
1
T_{2}=MT_{1}
T2=MT1,所有乘法都是在低抽样率下进行了。根据FPGA实现过程中速度与面积互换原则,降低运算速率,意味着可以减少芯片逻辑资源。
3. 多相抽取器的MATLAB实现
clear all; clc, close all;
%% 参数初始化
fs=8e3;%原始信号采样率
fc=[1e2,6.5e2,7e2];%信号频点,必须混叠内和外各有一个信号
p=[0,0,pi/2];%信号初始相位
a=[1,1,0.6];%信号幅度
D=8;%8倍抽取器
deAddF=[200,300];%抗混叠滤波器通带阻带
% deAddF=[fs/2/D/1.5,fs/2/D];%抗混叠滤波器通带阻带
phaseLen=512;%各相长度
signalLen=D*phaseLen;
%% 信号产生
[t,s]=cosSignalGen(fc,p,a,fs,signalLen);%plot(t,s,'.-') %采样1s产生叠加信号
x=awgn(s,100,'measured');%叠加噪声
%% 原型滤波器设计--Parks–McClellan算法
[n0,f0,m0,w]=remezord(deAddF,[1,0],[0.001,0.001],fs);%原型滤波器阶数计算%原型滤波器阶数 - [通带f,阻带f],[通带A,阻带A],[通带波纹,阻带波纹],fs
n0=ceil(n0/D)*D*2;%取I的整数倍,控制长度为2的整数倍,这样滤波延迟比较好计算
b=remez(n0,f0,m0,w);%计算原型滤波器系数
%% 信号频谱和滤波器响应
figure(1),subplot(311),title('信号频谱和滤波器响应');
[sf,sp]=myPsdCal(s,fs,length(s)); %计算叠加信号的功率谱
[bf,bp]=myPsdCal(b,fs,length(b));%计算滤波器幅频响应
plot(sf,sp,'bo-',bf,bp,'r.-'), legend('信号频谱','滤波器幅频响应');
xlabel('f/Hz');ylabel('A/dB');axis tight;
% 对原型滤波器进行多相分解
h=reshape(b(1:(end-1)),D,[]);%h(k,r)=b((r-1)*I+k);
%% 多相结构滤波---没有采样率变换就没有多相结构!!因此源采样率时用不着多相结构!
xp=reshape(x,D,[]);%多相结构的输入
y2=zeros(D,signalLen);%输出
for k=1:D
% delay=round((size(h,2)-1)/2);%滤波延迟---各个滤波器自己的延时都是其长度的一半
delay=size(h,2)/2-1;%滤波延迟---各个滤波器自己的延时都是其长度的一半
ytmp=conv(xp(k,:),h(k,:));%频域滤波
ytmp=circshift(ytmp,[0,-delay]);%去除延时
y1(k,:)=ytmp(1:phaseLen);%取信号时长
y1tmp=repmat(y1(k,:),D,1);
y2(k,:)=circshift(y1tmp(:),[k-1,0]);
end
y=sum(y2,1);%求和
ty=(0:1:signalLen-1)/fs;%采样时长
%% 时域波形绘制
point=64;
figure(1),subplot(312),title('原始信号和多相滤波时域图');
plot(t(1:D*point),x(1:D*point),'k.-',ty(1:D*point),y(1:D*point),'ro-'),
legend('原始信号','多相滤波信号');
xlabel('t/s');ylabel('A/v');axis tight;
%% 频谱波形绘制
figure(1),subplot(313),title('原始信号和多相滤波频谱');
[xf,xp]=myPsdCal(x,fs,length(y)); %计算原始信号的功率谱
[yf,yp]=myPsdCal(y,fs/D,length(y));%计算多相滤波后信号的功率谱
plot(xf,xp,'kp-',yf,yp,'ro-'),
legend('原始信号功率谱','多相滤波信号的功率谱');
xlabel('f/Hz');ylabel('A/dB');axis tight;
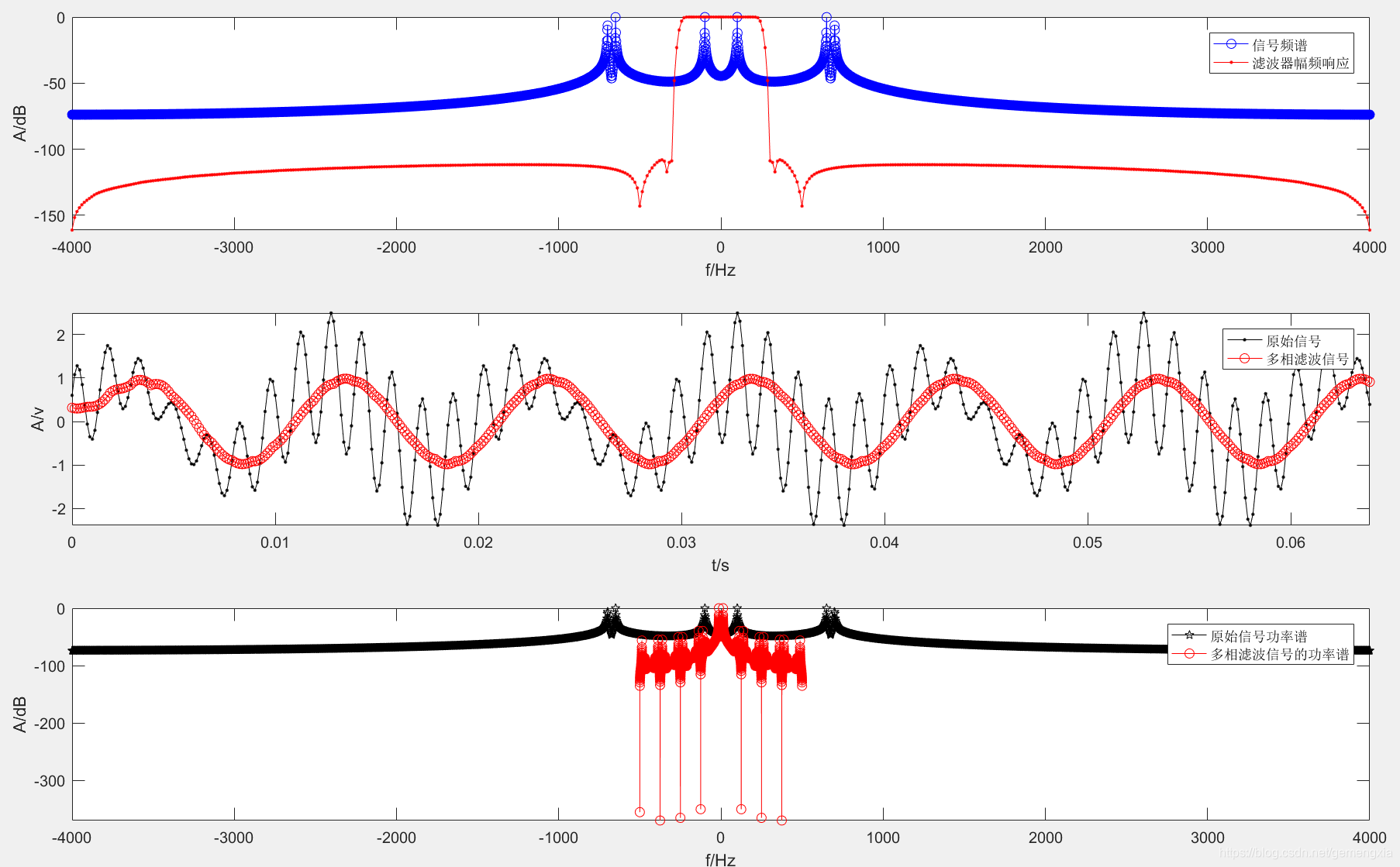





 本文详细介绍了多相分解技术在整数倍抽取中的应用,阐述了多相抽取器的结构及其MATLAB实现过程。通过多相分解,能够减少计算量,提高信号处理效率。文中还提供了具体的MATLAB代码示例,展示了一个8倍抽取器的设计与滤波过程,包括信号产生、原型滤波器设计和多相结构滤波的步骤。
本文详细介绍了多相分解技术在整数倍抽取中的应用,阐述了多相抽取器的结构及其MATLAB实现过程。通过多相分解,能够减少计算量,提高信号处理效率。文中还提供了具体的MATLAB代码示例,展示了一个8倍抽取器的设计与滤波过程,包括信号产生、原型滤波器设计和多相结构滤波的步骤。
















 2863
2863










