FSK调制解调

最新推荐文章于 2025-09-30 10:06:02 发布

原创

最新推荐文章于 2025-09-30 10:06:02 发布 · 7.5w 阅读

681 ·

CC 4.0 BY-SA版权

该文章已生成可运行项目，

文章目录

1.FSK调制解调原理

1.1FSK时域信号

数字频率调制（FM）是利用载波的频率传输信息的一种调制方式，其中最简单的是二进制频移键控（2FSK）。FM分为非连续相位FSK和连续相位FSK（CPFSK），两者的区别在于码元转换时刻的载波相位是否连续。

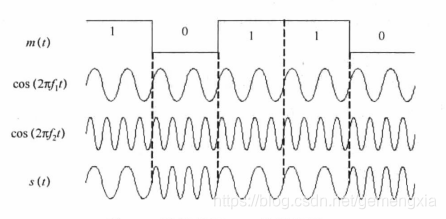
2FSK信号波形如下图所示，信号可以看成是频载为f1和f2的两个振幅键控信号的合成，2FSK信号可表示为：
在这里插入图片描述
式中，

式中，A是载波振幅，Tb为数字码元周期，{bn}为所传送的数字序列。

相位连续的FSK信号在码元转换时刻的相位是连续的，波形如下图所示。

此时调频信号可以表示为：

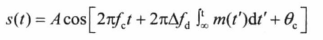
式中，fc是未调载波的频率，\delta fd是频偏因子。当m(t)为归一化基带信号时，\delta fd为峰值频偏，令
在这里插入图片描述
式中，h为调制指数或频移指数。

1.2相关系数与频谱特性

设FSK信号在一个码元期间内的波形为：
在这里插入图片描述
这两个信号波形的相关系数定义为：

式中，

则带入上式有：

通常

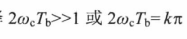
则相关系数简化为：

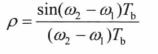
其波形变化图如下所示：

从图中可以看出，两个信号的相关系数在k*pi的时候为零，也就是说它们具有正交特性。

CPFSK信号的功率谱形状直接由调制指数h确定。当h=0.5时，功率谱曲线为单峰；当h=0.715时，功率谱曲线呈现双峰；当h=1时，功率谱曲线的双峰变成了两条线状谱，且每条线状谱所占的功率都是信号功率的1/4，与离散相位2FSK信号的功率谱曲线相同；当h>1时，双峰的距离逐渐增加。

1.3非相干解调

1.3.1相乘微分型AFC环解调法

AFC环是一个负反馈系统，从电路结构上看，AFC环主要由三种结构形式，比较广泛的是相乘微分型AFC环路。其架构如下图所示：
在这里插入图片描述
如果接收信号与本振信号存在频差，则在一定时间间隔内必然存在相差，将鉴相器输出的相位误差信号微分后，得到反映频差的误差信号，此信号经环路滤波器平滑处理后，控制VCO/NCO的振荡频率向输入信号频率靠近，最终使得频差近似为零。
设输入信号
在这里插入图片描述
VCO输入信号

则

显然有

当输入信号为单载波信号时，

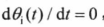
故有

上式反映了输入信号和VCO输出信号的频差。对于FSK信号来讲，上式即为调制信号，对其进行滤波判决，即可完成FSK信号的解调。

1.3.2包络检波解调法

2FSK信号的包络检波法解调方框图如下，可以视为由两路2ASK解调电路组成。这里的两个带通滤波器起分路作用，用以分开两路2ASK信号。上支路对应
在这里插入图片描述
下支路对应

经包络检测后分别取出他们的包络m1(t)和m2(t)。将两路滤波后的包络信号相减，在经过抽样判决，当判决值大于等于0时，判决为1，否则判决为0；

1.4相干解调原理

1.4.1最佳FSK相干解调器

最佳解调器结构如下图所示，在接收端产生一直信号s1(t)和s2(t)的波形，分别将其与输入波形y(t)在相乘器中相乘，再进行积分。在t=Tb时刻，将两积分器的结果取样，并在比较器中比较判决。因为解调器是对接收码元逐个进行处理的，故在每个码元的终止时刻，在取样之后要将积分器清零，以便接着处理下一个码元。
在这里插入图片描述
相干载波s1(t)和s2(t)通常需要采用载波锁相环路提取，位同步信号则需要专门的位同步锁相环路提取。

1.4.2易于实现的FSK相干解调器

1.4.1中的结构难以实现，通常采用下图结构实现：
在这里插入图片描述
FSK相干解调与ASK相干解调相似，FSK只是在用带通滤波器将信号分成上下两路后，在判决输出前增加一个减法器即可。

2.FSK的MATLAB仿真

2.1FSK信号产生

参数要求：非连续相位和连续相位的2FSK调制信号；调制度分别为0.5、0.7157、1、3.5；基带信号符号速率Rb=1Mbps；载波频率fc=6MHz;采样频率fs=32Rb；
源码：

ps=1*10^6;  %码速率为1MHz
N=1000;       %数据码元个数
Fs=32*10^6; %采样速率为32MHz
fc=6*10^6;  %载波频率为6MHz
Len=N*Fs/ps;

%仿真调制指数为0.5时的FSK信号
m=0.5;        %调制指数
freqsep=m*ps; %FSK信号中，两个频率之间的间隔
nsamp=Fs/ps;  %每个码元的采样点数
x = randint(N,1,2); % 产生随机数据做为数据码元
ContData = fskmod(x,2,freqsep,nsamp,Fs,'cont');       % 产生连续相位FSK调制信号的正交基带数据
DisContData = fskmod(x,2,freqsep,nsamp,Fs,'discont'); % 产生非连续相位FSK调制信号的正交基带数据
%将基带FSK信号正交上变频至6MHz中频
t=0:1/Fs:(Len-1)/Fs;
f0=cos(2*pi*fc.*t)+sin(2*pi*fc.*t)*sqrt(-1);
Contfsk=real(ContData.*f0');
DisContfsk=real(DisContData.*f0');
%计算FSK信号的幅频特性
m_ContFsk=20*log10(abs(fft(Contfsk,2048)));
m_DisFsk=20*log10(abs(fft(DisContfsk,2048)));;
m05_ContFsk=m_ContFsk-max(m_ContFsk);
m05_DisFsk=m_DisFsk-max(m_DisFsk);

%仿真调制指数为0.715时的FSK信号
m=0.715;        %调制指数
freqsep=m*ps; %FSK信号中，两个频率之间的间隔
nsamp=Fs/ps;  %每个码元的采样点数
x = randint(N,1,2); % 产生随机数据做为数据码元
ContData = fskmod(x,2,freqsep,nsamp,Fs,'cont');       % 产生连续相位FSK调制信号的正交基带数据
DisContData = fskmod(x,2,freqsep,nsamp,Fs,'discont'); % 产生非连续相位FSK调制信号的正交基带数据
%将基带FSK信号正交上变频至6MHz中频
t=0:1/Fs:(Len-1)/Fs;
f0=cos(2*pi*fc.*t)+sin(2*pi*fc.*t)*sqrt(-1);
Contfsk=real(ContData.*f0');
DisContfsk=real(DisContData.*f0');
%计算FSK信号的幅频特性
m_ContFsk=20*log10(abs(fft(Contfsk,2048)));
m_DisFsk=20*log10(abs(fft(DisContfsk,2048)));;
m07_ContFsk=m_ContFsk-max(m_ContFsk);
m07_DisFsk=m_DisFsk-max(m_DisFsk);

%仿真调制指数为0.715时的FSK信号
m=1;        %调制指数
freqsep=m*ps; %FSK信号中，两个频率之间的间隔
nsamp=Fs/ps;  %每个码元的采样点数
x = randint(N,1,2); % 产生随机数据做为数据码元
ContData = fskmod(x,2,freqsep,nsamp,Fs,'cont');       % 产生连续相位FSK调制信号的正交基带数据
DisContData = fskmod(x,2,freqsep,nsamp,Fs,'discont'); % 产生非连续相位FSK调制信号的正交基带数据
%将基带FSK信号正交上变频至6MHz中频
t=0:1/Fs:(Len-1)/Fs;
f0=cos(2*pi*fc.*t)+sin(2*pi*fc.*t)*sqrt(-1);
Contfsk=real(ContData.*f0');
DisContfsk=real(DisContData.*f0');
%计算FSK信号的幅频特性
m_ContFsk=20*log10(abs(fft(Contfsk,2048)));
m_DisFsk=20*log10(abs(fft(DisContfsk,2048)));;
m1_ContFsk=m_ContFsk-max(m_ContFsk);
m1_DisFsk=m_DisFsk-max(m_DisFsk);


%仿真调制指数为3.5时的FSK信号
m=3.5;        %调制指数
freqsep=m*ps; %FSK信号中，两个频率之间的间隔
nsamp=Fs/ps;  %每个码元的采样点数
x = randint(N,1,2); % 产生随机数据做为数据码元
ContData = fskmod(x,2,freqsep,nsamp,Fs,'cont');       % 产生连续相位FSK调制信号的正交基带数据
DisContData = fskmod(x,2,freqsep,nsamp,Fs,'discont'