浅谈字符串（模式串）匹配算法（BF与KMP算法）（C++实现）

【前言】

相信不少学过数据结构的同学有过被KMP算法劝退的经历吧，其实我也一样！记得四月份学到这个算法的时候，自己对于字符串的特性了解很浅薄，再加上这个算法的实现确实太过抽象，引入各种各样的变量和辅助空间看得人眼花缭乱，当时自己只能灰溜溜地把这个知识点直接放弃了，直到后来开始看算法大神左程云老师的课程解开了不少当时的困惑，所以本文会采用左程云老师的思路来介绍，这篇文章也算是我自己学习笔记的一个分享（安利一波左神，适合有基础的爱好者去听，会颠覆很多对基础算法的固有认知。）不得不说在目前学到的所有算法中KMP一定算得上难度系数较高的类型了，不少企业也出现过“手撕KMP”之类的笔试题。在这里有点惶恐，因为自己确实曾经被这个算法“劝退”过，鼓起勇气介绍这个算法也确实是对自己的一个挑战。在此我也会尽全力对算法中的细节进行拆解和描述！和我一起多画图多举实例，可能会更有助于对该算法的理解。

【情景引入】

在开始我们的介绍之前，我们先来看一道leetcode题目，虽然这是一道”简单题“，但是其背后的“水”可以说很深，且看分解：

28.找出字符串中第一个匹配项的下标-力扣（LeetCode）

题目描述的意思是给你两个字符串。这里举个实例说明，str1="Ilovealgorithm"(主串),str2="algorithm"（模式串），让你在主串中寻找与模式串中第一个匹配项的下标。在本例中，我们可以看出，str1完全包含了str2的完整内容（即str2是str1的子串）。在我们确定str1已经完全包含了str2，没有出现缺字漏字的情况下（举例：假如str1不变，str2="agorithm"(此时出现了缺字情况）），我们返回主串中所含子串第一次出现的位置。在本例中这个位置便是5（a对应的位置）。其实在一篇文章中，我们也常常利用这个算法来定位关键字。那么我们如何通过设计算法来实现这个过程呢？

一.BF算法-暴力解法

【算法思路】

BF算法的思路是：①从主串的每一个字符开始，依次与模式串中的字符进行匹配

②若成功匹配，则继续比较下一个字符。若不匹配，则需要对主串回溯，继续进行比较。我们对这个回溯过程进行举例说明：

S（主串）：abcfddcad

T（模式串）：abca

假设由i变量遍历S串，j变量遍历T串。从上面的实例可以看出，如果从主串的第一个字符（即'a'，我们将此位置记作k）开始匹配，S与T前三位是匹配成功的，但是第四位上S串是f，T串是a，匹配失败。此时对于模式串，回溯到首元素。对于主串，回溯到当前元素的下一个元素（k+1位置，即‘b’）开始匹配。

③直到主串中一个连续的字符序列与模式串成功匹配（用长度相等来体现），算法结束。

假设n为主串长度，m为模式串长度，则该算法的平均时间复杂度为O（n*m）。

【代码实现与注释解析】

由于本算法思路简单，限于篇幅，本文重点讲解KMP算法的思路，因此在此直接给出BF算法的代码实现：

int BF(const string& S,const string& T){
	//我们假定S为主串，T为模式串
    int i=0,j=0;//用i来遍历主串S，j来遍历模式串T
	while(i<S.size()&&j<T.size()){
		if(S[i]==T[j]){//如果成功匹配，则继续向后比较
			++i,++j;
		}else{//匹配失败，回溯
			i=i-j+1;
			j=0;
		}
	}
	if(j==T.size()){//模式串遍历完毕，匹配成功
        return i-T.size();
	}else{//匹配失败
        return -1;
	}
}

二.KMP算法

由前面的BF算法我们知道，对于每一次匹配过程，只要匹配失败便会进行回溯操作，大量的回溯操作无疑是耗时的，所以我们的一个改进思路是：能否减少回溯次数。1977年，三位科学家发现了这个更高效的模式串匹配算法，并分别用他们名字的首字母进行命名，故称为KMP算法。

【思路详解】

在介绍KMP算法之前，我们必须引入一系列概念。别慌！跟住我的节奏，结合图例来理解这些概念，才能更透彻地理解这个算法！

【最大前后缀匹配长度k】

我们首先在单个字符串上探索规律。对于一个字符串，我们将从它的首部出发产生的子串称为“前缀”，将从它的尾部出发产生的子串称为“后缀”（前后缀既不能为空，也不能包含所有元素）。我们引入一个整型变量k，来记录最长前后缀的匹配长度。这个变量与当前字符本身无关，而与当前字符前面的子串有关。我们结合实例来看：

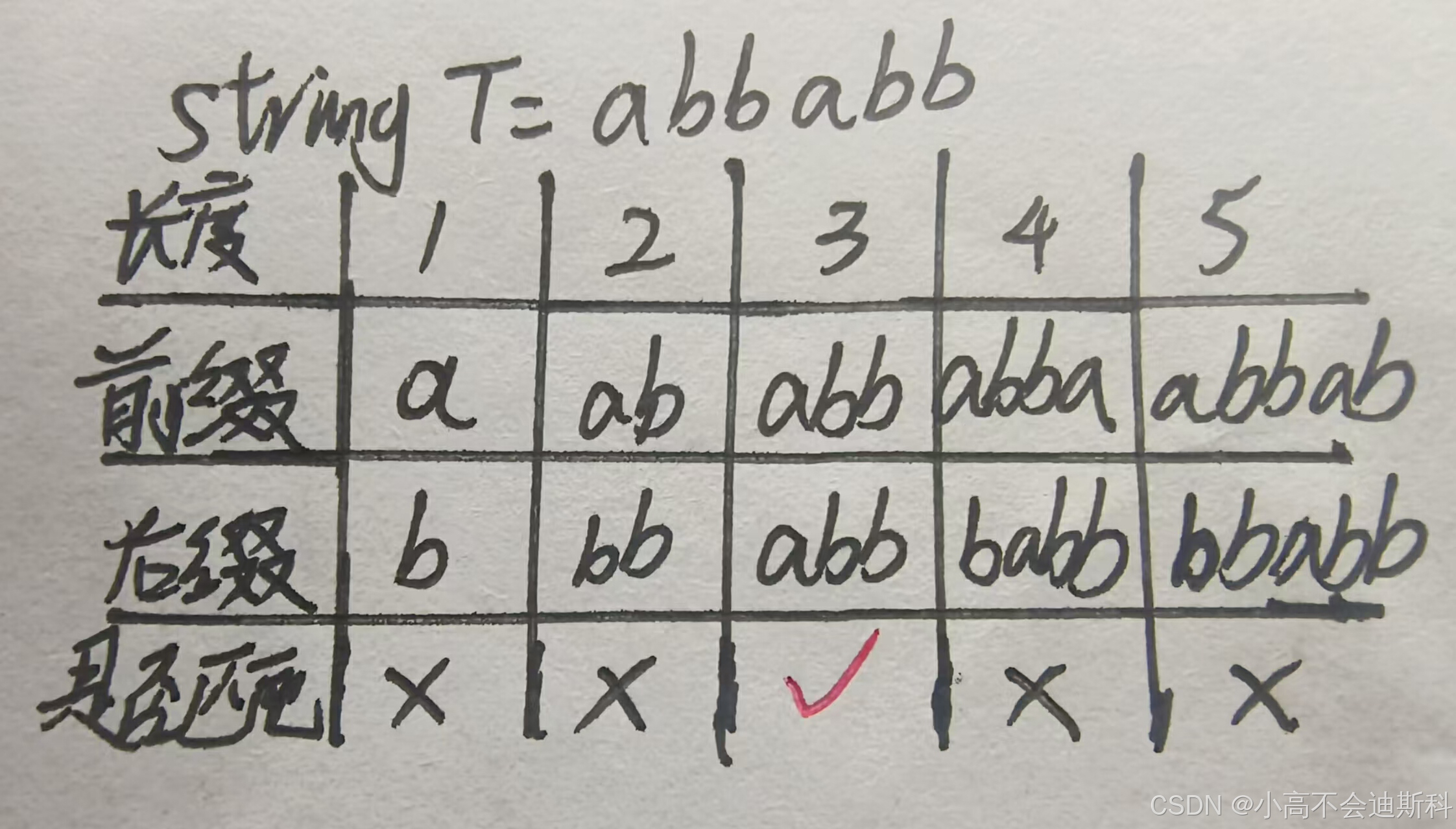对于字符串“abbabb”，结合上面表格来看，当长度等于3时，该串的前缀和后缀匹配，且匹配长度最大。所以此时k=3。而这个k是对谁而言的呢？假设我们在T串后面加一个字符‘c’，即T串变成“abbabbc”，这个k信息便是针对c而言的！，也就是说k信息是用来描述当前字符的前面所有字符构成的子串的。那么很显然，针对这个字符串的每一个字符，我们都能获取到它的“k信息”！我们将每个字符的k信息存储在一个数组里，我们将这个数组称为next数组。

【next数组的定义】

根据上面的描述，相信大家已经了解了next数组是怎么实现的，里面记录的是什么信息。那么在next[j]数组的实际构建中，会有以下三种情况：

①当j=0时，我们人为规定next[0]=-1。（在0之前根本没有字符串）

②当j=1时，我们人为规定next[1]=0。（前后缀不能包含整体，所以取0）

③其他情况，next[j]=k。

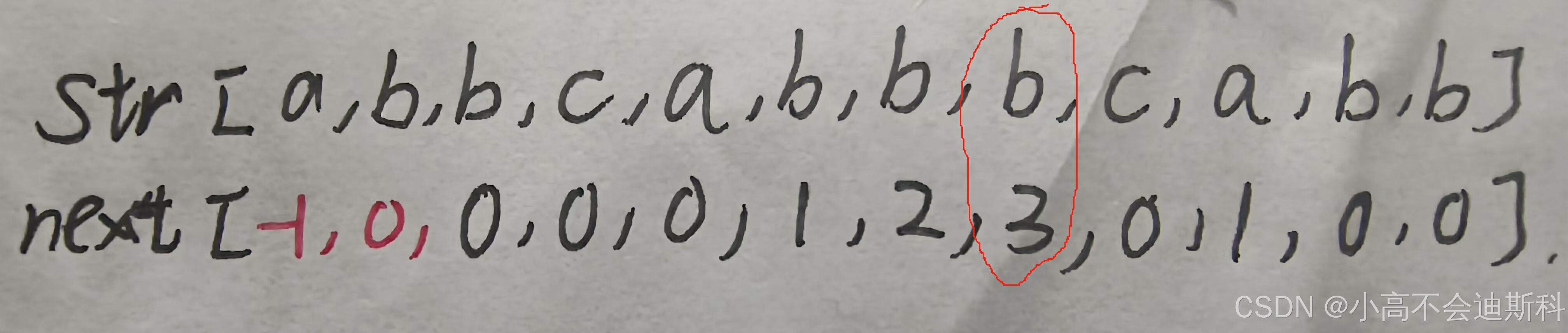
对应字符串str，我们根据上面给出的法则写出了下面的next数组。为方便理解，我举一个局部的例子来看：注意看红圈的位置，对应位置下标为7，此时next数组记录的是[0,6]范围上的k信息，不难发现对于这个子串k信息的值为3。其他位置的推导与之同理，篇幅有限不再赘述。

这里先建立一个概念：无论是求k信息，还是构建next数组，都是针对模式串进行的！

【BF算法的小加速-KMP算法】

回到我们前面的字符串匹配问题。我们假设S为主串，T为模式串。在前面所讲的BF算法中，只要发现二者匹配失败便会回溯到头，这样是很低效的。我们分别对S从i位置开始（用p1），对T从0位置（用p2）开始遍历（因为T是S的待匹配模式串，结合BF算法的回溯过程进行理解）。我们假设p1来到X位置，p2来到Y位置时，两串开始不匹配，如下图所示：

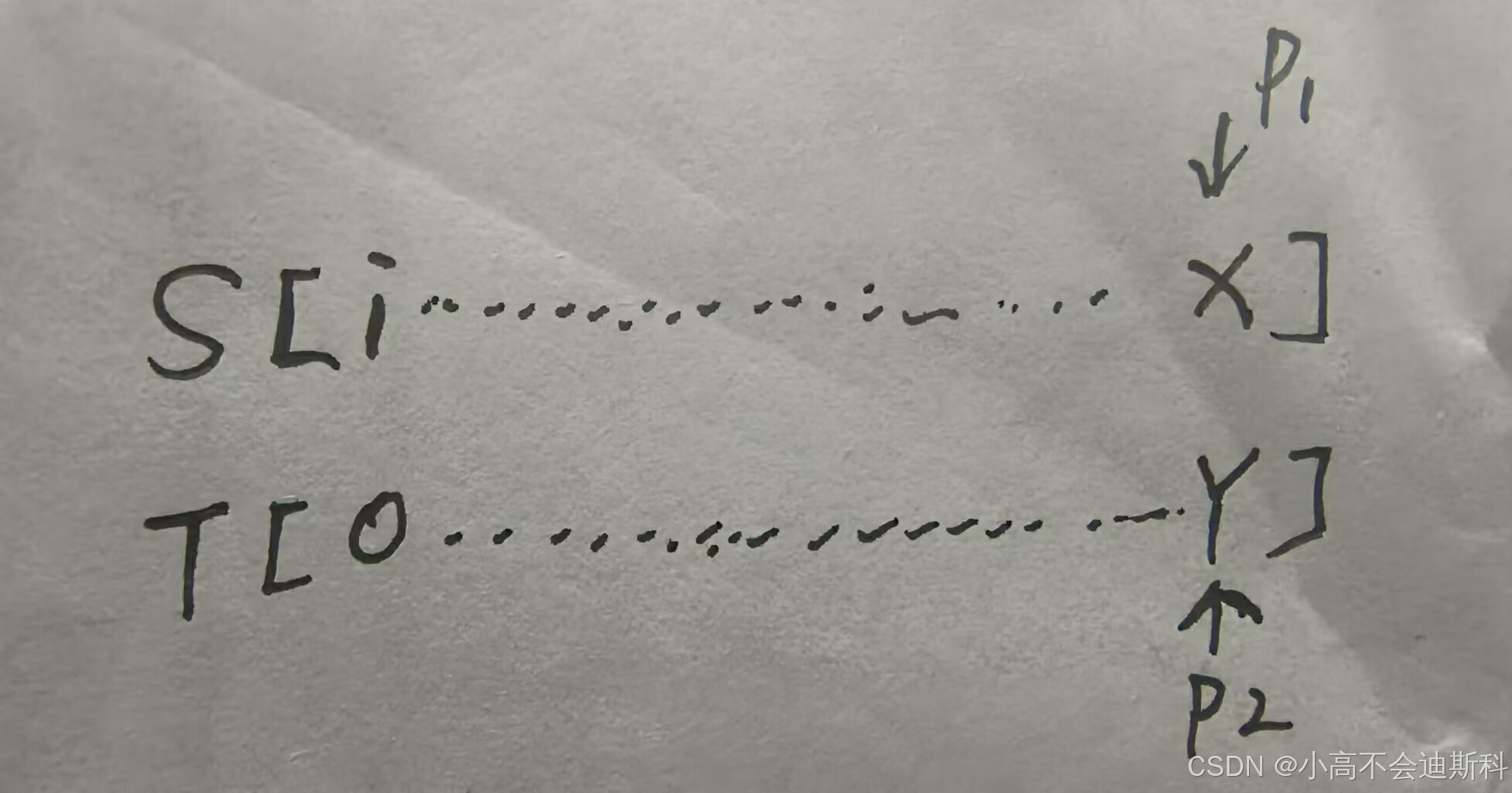
首先先声明：此处为方便理解，我们用下标来代替实际元素！而且S,T两串不止这么长，只是从X,Y位置开始匹配不上了。这里有一个很重要的潜台词，也就是在X,Y对应的位置之前，S,T两串是完全匹配的！

KMP算法的做法是：X保持不动，Y来到“前缀与后缀匹配时的最大前缀”之后的位置（该位置通过访问next数组得到）记作Y'，之后从S串的X位置和T串的Y'位置开始继续匹配，如下图所示：

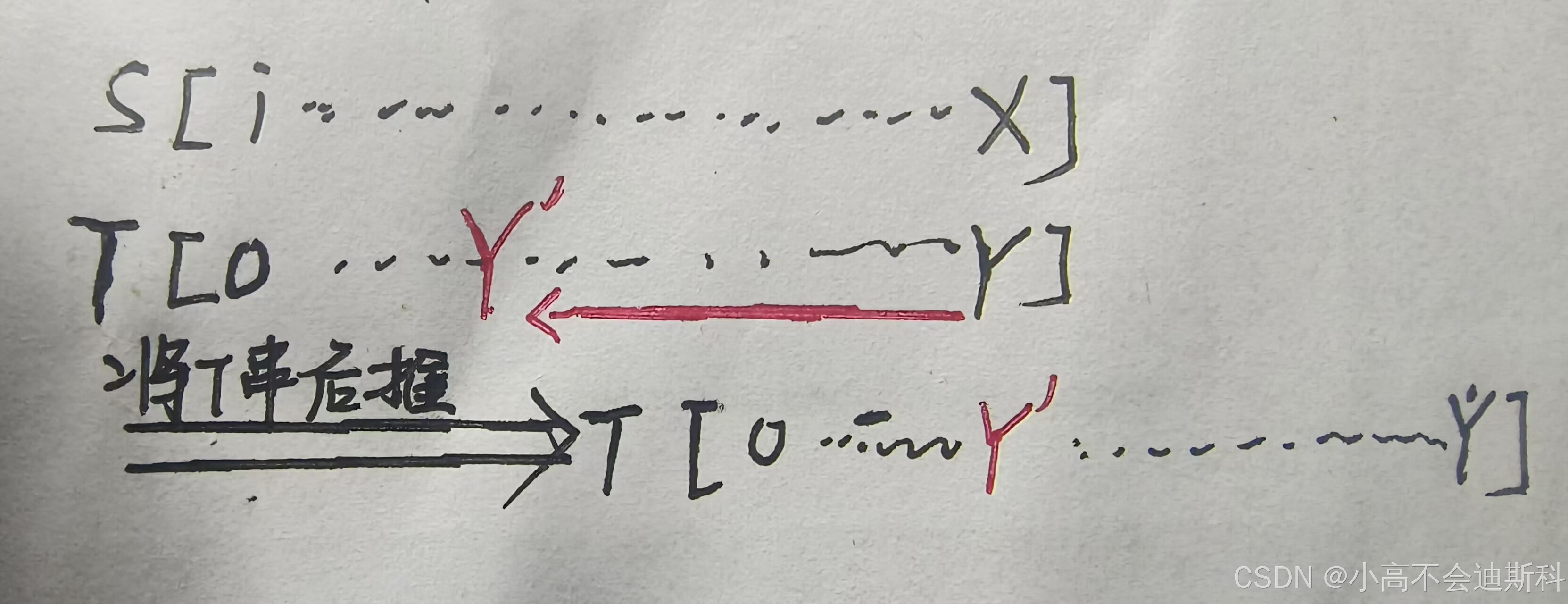
从图中我们不难看出，实际效果就是将T串整体向后推，再进行匹配。其实我们此时已经可以发现其中的一些小“端倪”，KMP不再和BF一样，当匹配失败就立即回溯到头。但是，为什么可以不再回溯到头呢，理论依据是什么？此时我们需要结合实例来看，会更明朗一些！

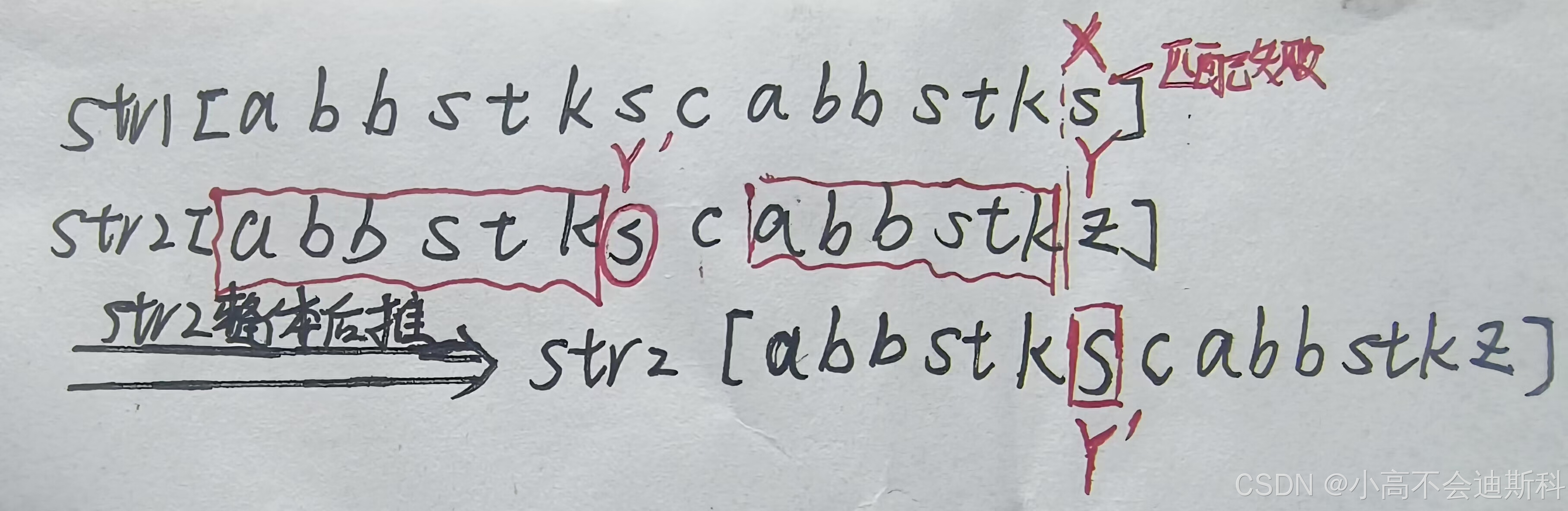
我们拿到了主串str1（理解成前文的S串）和模式串str2（理解成前文的T串）。这里我们必须先声明一点：在实例中串中的元素是实际内容，而不再是前文所指的下标。str1的前面可能还有元素，也就是说这个str1片段的起始元素下标不为0，而str2的起始元素下标为0！，接下来我们来看，显然，当p1=X,p2=Y时，两串匹配失败。此时通过查询next数组，我们发现，在模式串str2中最大前后缀匹配长度为6（本例中这个前后缀为“abbstk”），那么依照前文所讲述的，Y'会来到最大前缀的后一个位置，也就是红圈圈起来的s处。那么我们此时让X与Y’对齐进行后续匹配，这么做的原因是：对于str1，我能确保从i位置到m位置的任意位置（k）出发，配不出完整的str2(i,m见下图)。接下来大家可能会有疑问了，对于str1而言，难道从i位置到m位置出发，能确定配不出完整的str2吗？答案是：能！接下来我们解释：

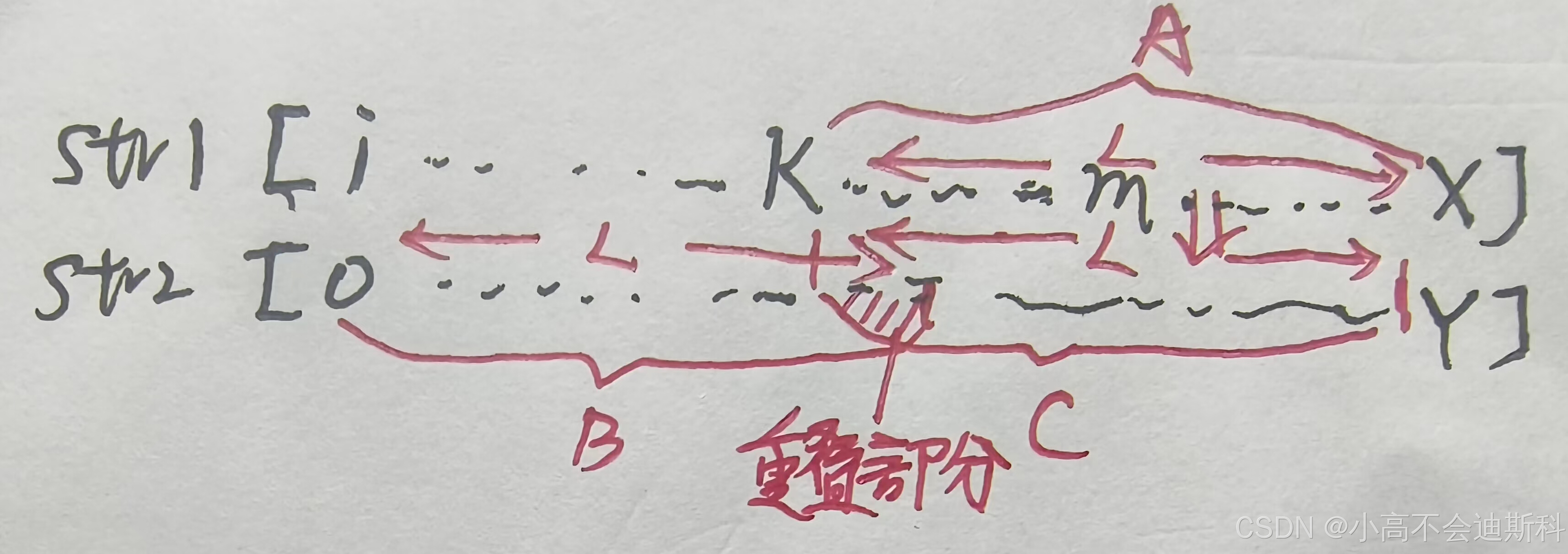
为了方便讲述，此处我们串中元素继续用下标代替。首先，当str1中的X与str2中的Y'对齐时，本质上，匹配的起点是：str1的m位置，str2中的0位置。对于上面的问题，我们采用反证法的思路：假设对于str1,从i位置到m位置的任意位置（k）出发可以配出完整的str2。那么首先需要保证：str1中的[k~X]部分（如图A部分）（假设长度为L）要匹配上str2中长度为L的前缀（如图B部分）。但是实际上，str1和str2在X,Y位置之前一路匹配。也就是说一定能从Y位置出发找到长度为L的后缀（如图C部分），且这个前后缀有重叠，产生矛盾，故假设不成立。那么最后一个问题来了，我们该如何构建next数组呢？

【next数组的构建】

其实next数组的构建过程类似数学归纳法的感觉，我们根据T串来构建next数组以记录k信息。首先next[0]和next[1]的值是我们人为确定的，分别是-1和1。然后next[2]的值是依据T[0]和T[1]来构建的，next[3]是根据据T[0]，T[1]和T[3]来构建的，依此类推。此时我们假设来到了i位置：

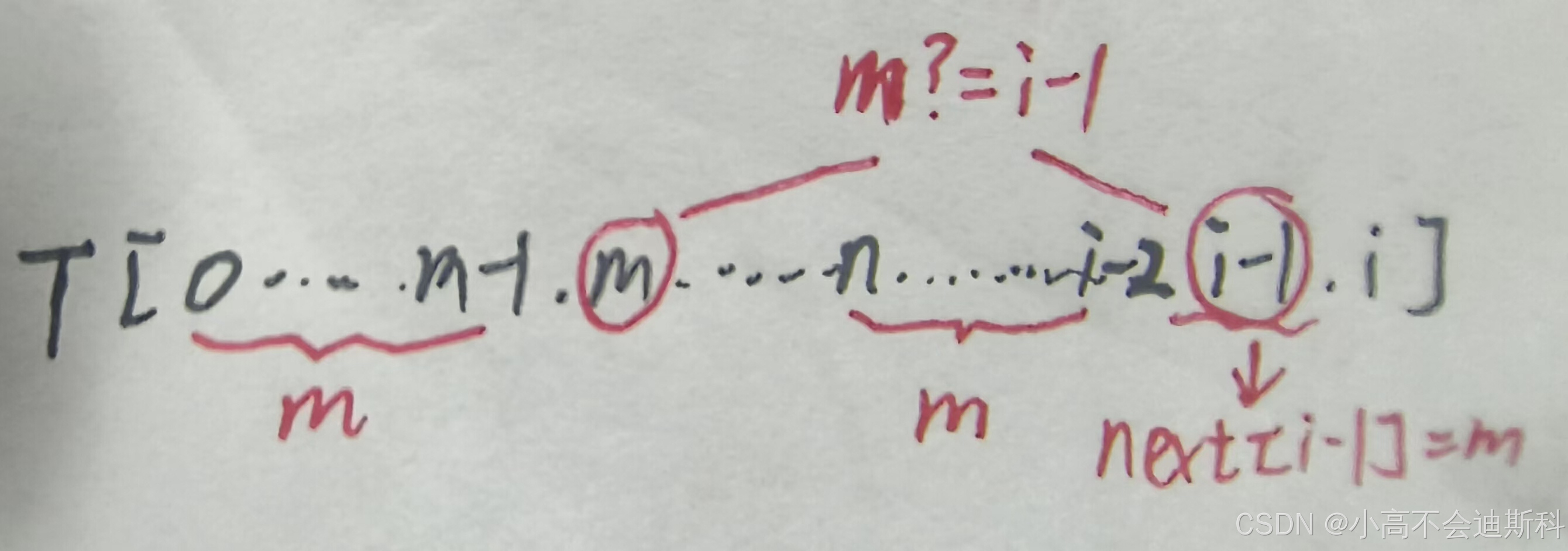
由前面的推导过程我们不难猜测，欲得出i位置的k信息，我们首先要知道i-1位置的k信息，假设i-1位置的k信息为m，即在[0~i-2]区间上最大前后缀匹配长度为m（结合上面图来看）。

①如果m处的元素等于i-1位置的元素，那么在[0~i-1]区间上最大前后缀匹配长度变为m+1，即此时i位置处的k信息为m+1。

②如果m处的元素不等于i-1位置的元素，则在[0,m-1]位置上继续寻找（即使用部分信息进行回退），与①步骤同理。此处有些抽象晦涩，我们举个实例来看：

由前面给出的结论，我们先判断e是否等于‘？’。如果相等，i位置处的k信息值为最大前缀长度+1=9（即next[i]=9），如果不相等，有点类似前面KMP算法的过程：我们在e元素所在位置之前的子串上面进行前后缀匹配，找到最大前缀之后的元素（即s），判断s是否等于‘？’，如果相等，i位置处的k信息值为最大前缀长度+1=4（即next[i]=4），如果不相等，则继续回退，重复这个过程。直到没有信息可匹配，next[i]便等于0+1=1。

到此，KMP算法的细节我们便介绍完毕。接下来举一个综合性比较强的实例来加深理解：

【综合实例】

首先我们来看第一次匹配：str1和str2在X,Y位置处匹配失败。那么我们通过查询next数组，确认Y位置处的next[Y]值为7，也就是说在Y前面的子串中最大前后缀的匹配长度为7。Y'来到最大前缀之后的位置，即下标为7的位置，接下来将X与Y'对齐进行第二次匹配。

第二次匹配：str1与str2在X,Y'位置处再次匹配失败，同理Y''来到下标为3的位置，接下来将X与Y''对齐进行第三次匹配。

第三次匹配：str1与str2在X,Y''位置处再次匹配失败，对于Y''位置查询next数组，发现前后缀不匹配（最大匹配长度为0），则Y'''来到0位置处，接下来将X与Y'''对齐进行第四次匹配。

第四次匹配：str1与str2在X,Y'''位置处再次匹配失败，此时已经不存在前后缀了。我们只能让str1从E位置开始，对应str2的0位置进行匹配了！

【代码实现与注释解析】

//构建next数组
vector<int> getNextArray(const string& T) {
    int l = T.size();
    vector<int> next(l, -1);  // 初始化 next 数组为 -1
    if (l == 1) {
        // 长度为 1 时，直接返回
        return next;
    }
    next[0] = -1;  // next[0] 不需要用于匹配，通常设为 -1
    next[1] = 0;   // T 的第一个字符和自身匹配，长度为 1 的前缀和后缀
 
    int i = 2, cn = 0;
    while (i < l) {
        if (T[cn] == T[i - 1]) {//使用i-1位置的信息进行比对
            next[i] = cn + 1;  // 更新 next[i]
            cn++;              // 移动 cn 到下一个可能的匹配位置
        } else if (cn > 0) {
            cn = next[cn];     // 使用部分匹配信息回退 cn
        } else {
            next[i] = 1;       // 没有前缀可匹配，next[i] 为 1
        }
        i++;  // 移动到下一个字符
    }
    return next;
}
//KMP算法主体函数
int KMP(const string& S,const string& T){
	int l1=S.size();
	int l2=T.size();
	if(l1==0||l2==0||l2<1||l1<l2){//字符串长度限制条件
       return -1;
	}
	vector<int> next=getNextArray(T);//获取next数组
	int p1,p2=0;//p1遍历S串，p2遍历T串
	while(p1<l1&&p2<l2){//p1,p2均未越界
       if(S[p1]==T[p2]){//匹配成功，指针后移即可
          p1++;
		  p2++;
	   }else if(next[p2]==-1){//T串中比对的位置已经无法往前跳了
          p1++;//只能找S串的下一个位置了
	   }else{
		  p2=next[p2];//这就是前面Y-Y'的过程，通过查询next数组得到位置实现跳转
	   }
	}
    if (p2 == l2) {
        return p1 - p2;  // 如果T串遍历完了，返回匹配开始的位置
    } else {
        return -1;  // 否则返回-1表示匹配失败
    }
}

【经典例题】

经典题--796.旋转字符串-力扣(leetcode)

请大家在看下文的模板代码之前，一定先浏览并理解链接中的题意。在此我对本题的题意再做一个大致的梳理：比如说有字符串“abcde”，那么它的旋转字符串就有“abcde”,“bcdea”,“cdeab”,“deabc”,“eabcd”这五种情况。我们需要判断任意两个字符串是否互为“旋转字符串”。依照上面给出的例子，我们将字符串“abcde”复制并自我拼接，得到字符串str=“abcdeabcde”，我们不难发现，上面的这些“旋转字符串”都是字符串str的子串。于是这个问题就被转化为了字符串匹配问题。接着采用我们上文介绍的KMP算法解决即可。

class Solution {
public:
    bool rotateString(string s, string goal) {
        if(s.size() != goal.size()) return false;

        string res = s + s;
        vector<int> next(goal.size());
        next[0] = -1;
        for(int i = 1, j = -1; i < goal.size(); i ++)
        {
            while(j != -1 && goal[j + 1] != goal[i]) j = next[j];
            if(goal[j + 1] == goal[i]) j ++;
            next[i] = j;
        }

        for(int i = 1, j = -1; i < res.size(); i ++)
        {
            while(j != -1 && goal[j + 1] != res[i]) j = next[j];
            if(goal[j + 1] == res[i]) j ++;
            if(j == goal.size() - 1) return true;
        }

        return false;
    }
};

不得不承认，KMP算法确实实现难度不小，而最有效的方法便是：重复举例理解之后手撕代码。这个过程中我们一定要有耐心，没有什么过不去的坎。我是小高，一名非科班转码的大二学生，水平有限认知浅薄，有不当之处期待批评指正，我们一起成长！