浅谈归并排序和快速排序（C++实现）

【前言】

前文我们介绍了三种时间复杂度为O（n^2）的排序算法，即选择排序，冒泡排序，插入排序。并称为“三大基本排序算法”。在引出本文要介绍的两种效率较高的排序算法之前，我们先引入一道经典的leetcode题目：

912. 排序数组 - 力扣（LeetCode）

不难注意到，这道题目的特别之处是给出了时间复杂度为O（nlogn）的限制，那么我们如果用之前介绍的“三大基本排序算法”会导致程序运行超时。所以我们需要选择性能更优的排序策略。本文所描述的两种排序算法有一定难度，建议先掌握一些基本的数据结构知识和前面的“三大基本排序算法”再回头来看。顺带一提，时间复杂度为O（nlogn）的算法还有堆排序，但是因为堆（优先级队列）的概念十分重要，是贪心算法中经常使用的解题技巧，我们将在后续出专题对堆结构及其应用进行详细介绍。

一.归并排序--由散及整，分而治之

【涉及思想】

分治，递归，二分，双指针

【思路与图例讲解】

当我们拿到了一个无序数组（这里我们假想数据量非常庞大），我们很难从这个总体来研究排列的策略，那么我们如果将这个庞大的数组不断拆分，在若干个子数组上研究，随着数据量的降低，排序的策略也就会变得明朗起来，就像品尝美食一样，一口吞下往往只能果腹，细嚼慢咽才能品得真滋味！这便是分治思想的实例。此时我们来想一种极端情况：当把一个数组分解为若干独立的数时，此时我们默认单个独立的数它就是有序的！之后我们将这些单个有序的数字按照某种规则进行合并，使合并形成的“子数组”内部是有序的。在不断合并的过程中，通过使这些子数组有序，从而最终达到使得整体有序的目的，这便是归并排序的核心思想。那么现在问题来了，该怎么去实现上述思路呢？

归--拆分

首先我们要将这个目标数组（假设长度为n）不断向下拆分，直到这个数组被拆分成了n个离散的数。那么我们要以什么标准进行拆分呢？没错，这就涉及到了我们的二分思想！我们每次以数组的中点作为“分水岭”（用变量mid存储），拆分成左右两边。这样看下去其实拆分步骤每一步都执行的是相同的操作，即找中点，拆分，再继续在拆分过的子数组上找中点。 此时我们便想到了应用递归思想来进行这个拆分操作（这便是“归”字的由来）。学过计算机组成原理或者汇编语言的同学应该知道，系统在内存预留了一块特殊的存储区域，叫做栈区，也称递归调用栈（函数调用栈）。这个区域专门用来存储这些后进先出（LIFO）的元素，函数的递归就是借助这个内存区域实现的。回到正题，在递归调用的过程中，其实我们已然在进行“不断寻找中点”的过程中把这个数组给拆分了。等到拆成n个离散的数的时候，因为单个数字一定是有序的，我们无法再拆分，此时我们开始执行合并！

并-合并

比起前面的“归”字，“并”字就如同它的字面意思一样好理解，但是它的实现还是略有难度的。首先前文有提到，我们合并数字需要达到局部有序的目的，那我们该如何保证合并的过程中局部有序呢？我们很难原地实现这件事，此时需要引入一个辅助数组（helper）对来自两个不同子数组的元素进行合并并且排序，此时我们便需要应用双指针的思想。由前文，我们按照“二分”的思想将整个数组不断拆分，那每个数组都有它的“左子数组”和“右子数组”。（没错，原理就是构建二叉树），我们定义两个变量p1,p2，分别指向两个子数组的首元素（注意不是指针变量，只是索引），定义一个i变量作为helper数组的索引。接下来我们结合下面图例来讲：

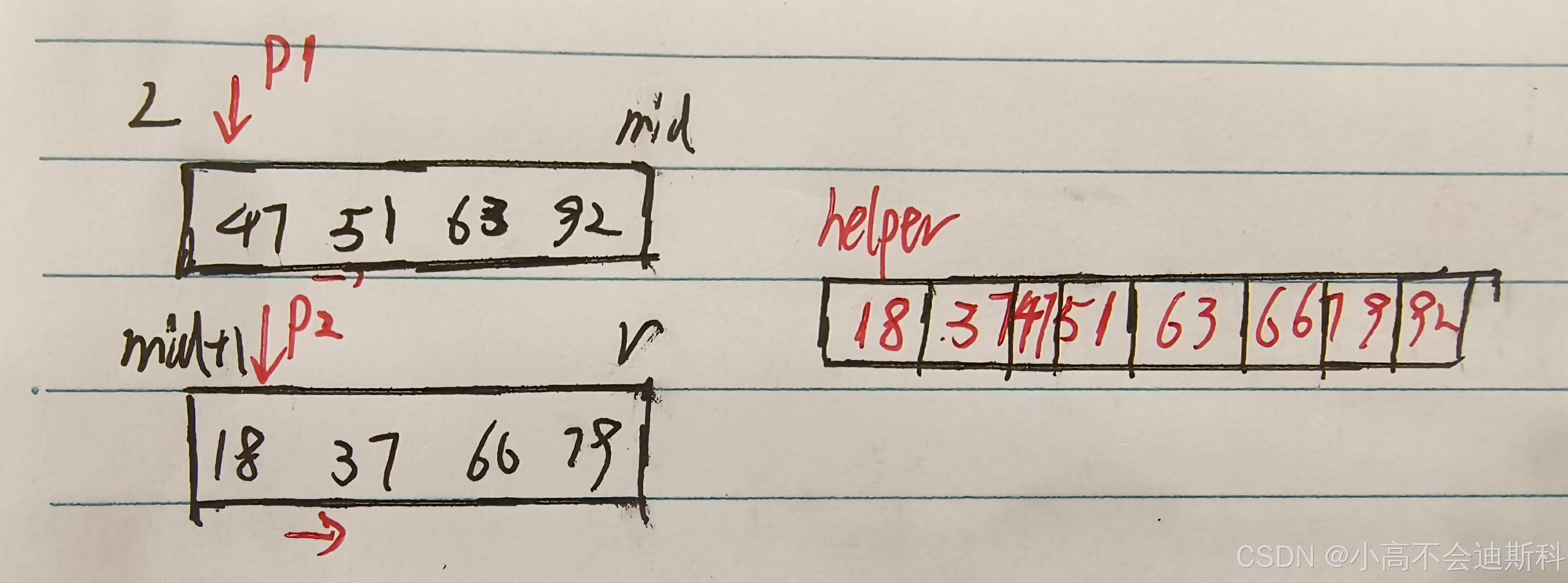
 由上面的图例我们不难看出，两个待合并的子数组（上面的子数组记作nums1,下面的记作nums2）已经有序（因为前面执行了相同的合并操作），接下来我们将p1与p2所指向的元素进行比较。注意一开始p1和p2都没有越界，因为18<47,所以我们将较小的那个也就是18拷贝到helper数组中。对于两个子数组来说，谁的元素被拷贝进了helper中，谁对应的指针（索引）向后自增，此时p2自增，i自增。之后的同理。直到79进入helper，此时nums2已经为空。p2自增，发生越界，则将nums1数组中剩余的所有元素拷贝到helper中。最终有借有还，helper数组也不是一个“无赖”，再将这个排好序的数组拷贝回nums（原数组）。我们的归并排序就结束了！

上图我们展示了归并排序的过程，不难发现在拆分的过程中我们数组之间构成了一棵完全二叉树，也就是一棵归并树。由二叉树的相关知识我们知道，假定这棵树由n个结点，那这棵树的树高是logn级别。又因为合并数组是线性级别的时间复杂度，归并排序的时间复杂度为O(nlogn),仅慢于快速排序，性能优于O（n^2）的排序算法。但是由于开辟了辅助数组，所以归并排序的空间复杂度为O(n)。归并排序算法的并行性很高，因为每个合并过程可以独立完成，互不牵涉。

【关键点梳理】

采用分治的思想，通过递归方法将两个或两个以上的“有序子序列”合并为一个有序序列。即以中点划分，先让左侧子数组有序，再让右侧子数组有序，最后进行整合。

【代码实现与注释解析】

void Merge(vector<int>& nums,int l,int mid,int r) { //合并函数
	vector<int> help(r-l+1);//辅助数组
	int i = 0;//i变量指向help数组首元素
	int p1 = l, p2 = mid+1;//p1,p2分别指向两个子数组
	while (p1 <= mid && p2 <= r) {//当p1,p2均未越界时，把p1,p2所指的元素小的那个拷贝进help数组中
		help[i++] = nums[p1] <= nums[p2] ? nums[p1++] : nums[p2++];
        //这是采用三目运算符的写法，意义是：
        //这里p1和p2所指向的数组逻辑上应该拆成两个数组来看，与图例同理
        //比较p1和p2所指元素的大小，把小的拷贝进help数组中
        //之后help数组和被拷贝元素数组的索引向后自增
	}
	while (p1 <= mid) { //当p2已经越界，而p1尚未越界时，将p1中剩余的元素拷贝进help数组中
		help[i++] = nums[p1++];
	}
	while (p2 <= r) { //当p1已经越界，而p2尚未越界时，将p2中剩余的元素拷贝进help数组中
		help[i++] = nums[p2++];
	}
	for (int j = 0; j < help.size(); j++) {
		nums[l + j] = help[j];//有借有还，将help中已经有序的部分拷贝回原数组
	}
}
void Process(vector<int>& nums,int l,int r) { //主过程函数
	if(l>=r){ //下标规则，不写会导致下标越界
        return ;
    }
	int mid = l + (r - l) / 2;//记录中间位置
	//这里拓展一种写法：int mid = l + ((r - l) >> 1)
	Process(nums, l, mid);//左半部分递归执行
	Process(nums, mid + 1, r);//右半部分递归执行
	Merge(nums, l, mid, r);//无法再分，开始合并！
}
void MergeSort(vector<int>& nums) { //主体函数
	if (nums.size() < 2) { //数组为空或者只有一个数，我们就没必要大费周章了
		return;
	}
	Process(nums, 0, nums.size() - 1);
}

二.快速排序--partition

【引入：什么是partition】

快速排序的一个关键词是partition--划分。也许当看到这么一个晦涩的词汇有朋友会感觉到摸不清头脑，但是如果想要弄懂快速排序的原理，我们必须知道什么是partition，以及该怎么去实现它。这里我们先来看一道经典的leetcode题目：

75.颜色分类-力扣（LeetCode）

根据题目所述，我们手中有一个数组，数组中的元素被涂上了三种颜色（红，蓝，白）。现在我们对它们进行原地排序（不借助额外空间），使得相同颜色的元素相邻。这种问题也习惯于称为“荷兰国旗问题”或“俄罗斯国旗问题”。

颜色这种抽象的量不便于比较调整，我们用数字对颜色种类进行标记，假设红色标1，蓝色标2，白色标3。那这个问题就转化为“使数值相同的元素在物理位置上相邻”。那么我们不妨以“2”作为基准，比它小的（即“1”）都放在它的左边，比它大的（即“3”）都放在它的右边。也许这么说不太严谨，但是重要的是get到这个过程的思想。没错，这就是partition，也就是快速排序的子过程！

【思路与图例讲解】

讲清楚了partition思想之后，我们便开始介绍快速排序的过程。其实快速排序也是基于交换的排序，是冒泡排序的改进。我们在某个无序数组上，基于某个数（我们将它记作pivot）进行上文介绍的partition操作，产生的效果是：比它小的数都来到了它的左边，比它大的数都来到了它的右边，但是值得注意的是，此时这个数的左右两侧并非有序，只是按照大小关系进行了初步划分。类似前文所讲的归并排序，假设以这个数（pivot）为“分水岭”，在它的左右两侧的子数组上递归执行partition操作，那么这个数组就会慢慢由局部有序变为整体有序，我们对整个数组进行排序的目的也就达到了！

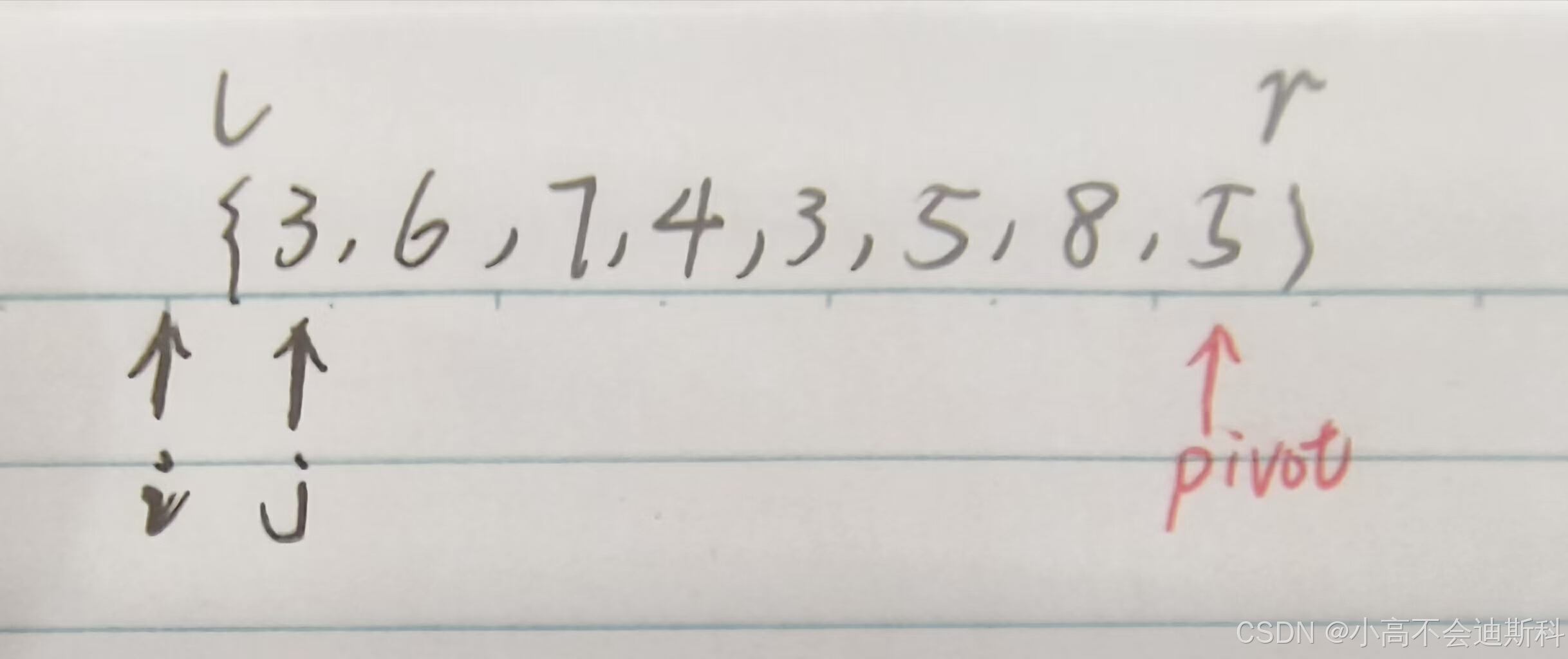
前文概念性的讲述比较抽象，接下来我们结合上面图例来看：我们拿到了一个如上图的左右边界为l,r的数组，现在我们假定最右边的元素5作为此次partition过程的主元（主元的选取问题后文介绍，此处先默认）。我们定义两个变量i,j作为数组下标的索引（双指针思想），i初始化为l-1而j初始化为l。为什么采用了这么一种不三不四的初始化方式呢？

首先我们先明确，我们用j变量来遍历数组并逐一比较所指元素与主元的大小，它标记的其实是“待比较的元素”，所以j从数组第一个有效位置开始移动，移动到主元之前（注意：我们不遍历到主元上），这很好理解，也符合我们的常识。而i变量用来标记小于等于主元（pivot）的最后一个位置，i左侧的区域其实就是小于等于主元的所有元素。由于初始化时还没有任何元素被比较，这个“待比较的元素”便是数组的首元素，也就是说此时i左侧的区域应当是空的，因此i指向l-1位置。我们来抽取几个过程进行分析：

当j=0时，nums[0]=3,因为3<=5，所以我们要把它放到i的左侧（即与i位置的元素发生交换）但是此时i指向空，属于无效访问，交换动作没有意义。所以我们通过让i自增来让i有效，也使得“3”成功进入i所划定的范围。宏观来看，这一步数组内部的元素顺序没有发生任何变化。此时j和i都处在0位置。

当j=1时，nums[1]=6,因为6>5,它不应到i所划定的范围当中，故不发生交换，i的位置也保持不动。j=2时同理，此处不再赘述。（！注意，此时i保持在0位置不动，也就是说只有触发交换条件，i才会移动）

当j=3时，nums[3]=4,此时4<5，触发了交换条件。nums[3]便与nums[1]进行交换，而i此时也通过自增运算移动到了1位置。情况如下图所示：

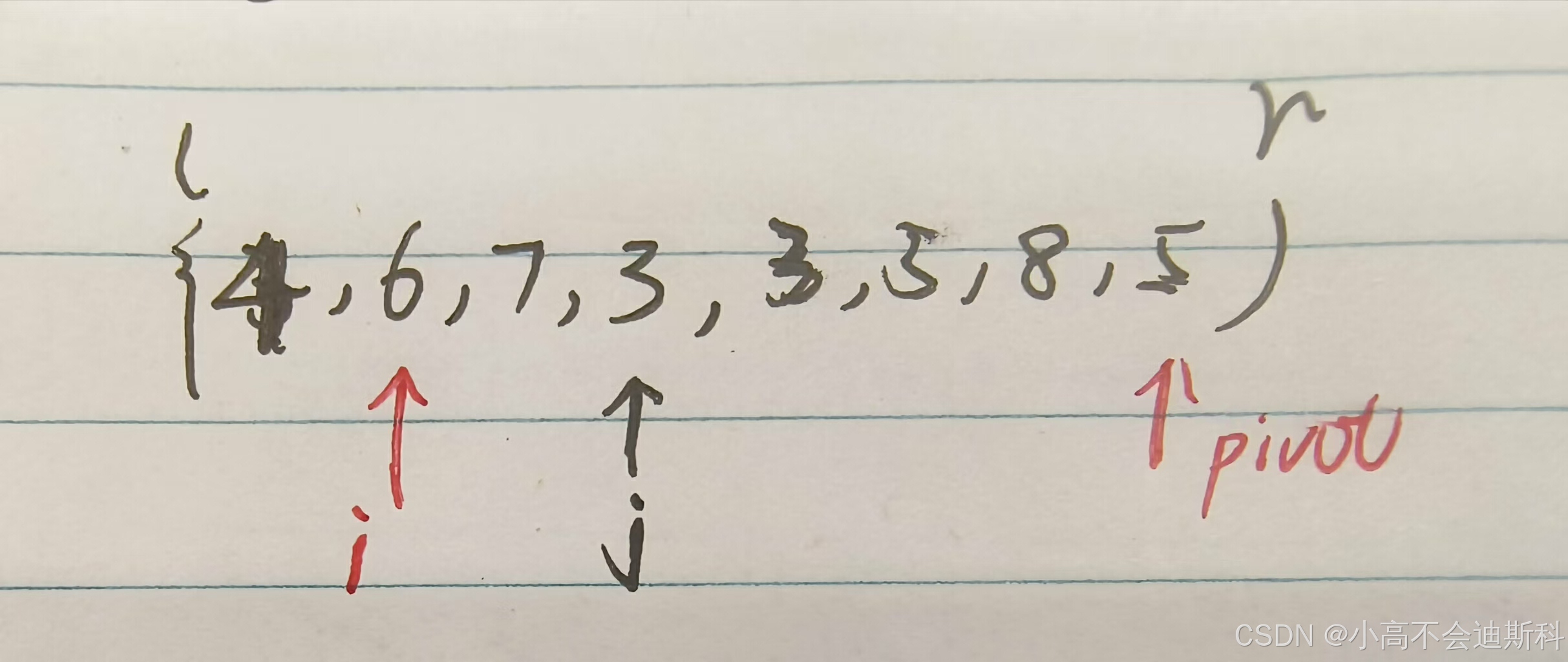
于是我们讨论完了两种大情况，后面的过程完全同理。当j变量遍历到主元之前的最后一个元素时，情况如下图所示：

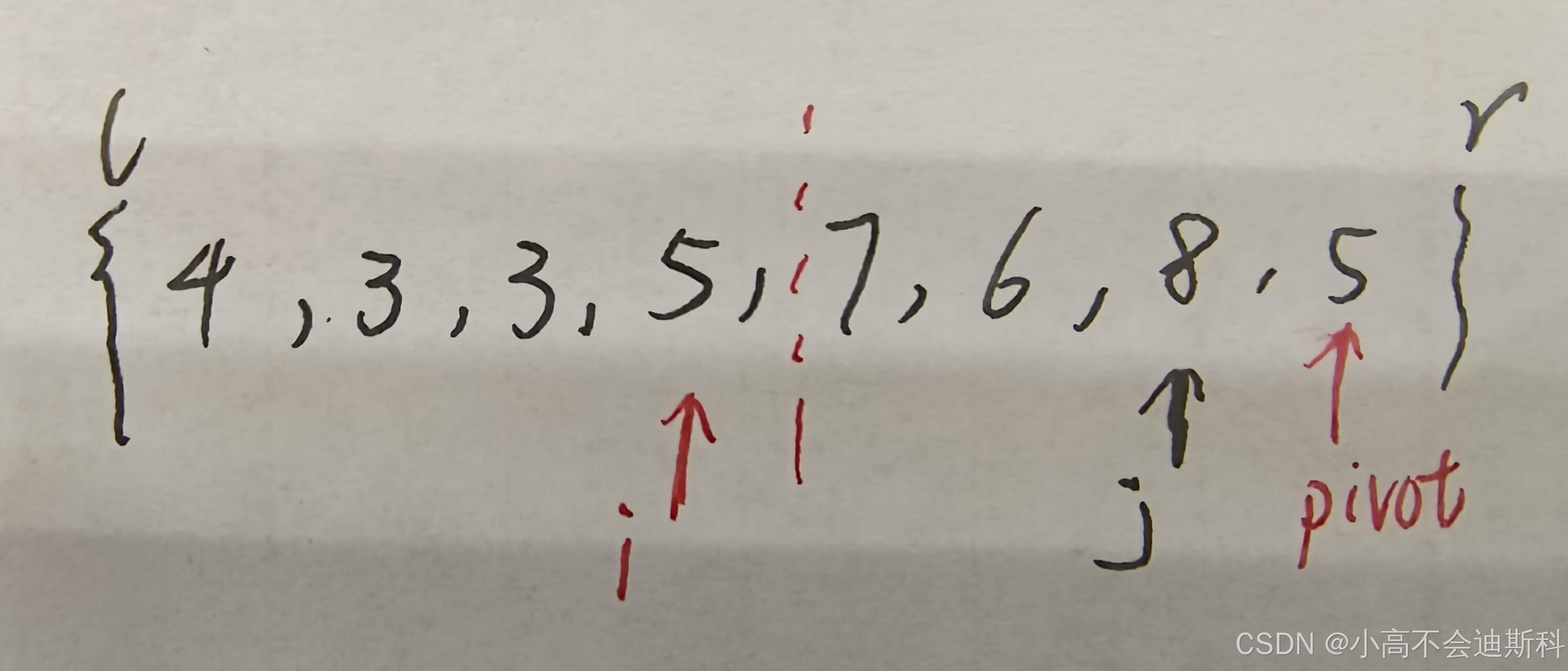
由上面图例我们不难看出，i位置的前面我画了一条虚线，这便是一个“分水岭”，在这个分界线之前的元素都<=5，之后的元素都>5。接下来我们便需要让这个主元回到它应该在的位置上，所以我们将主元与i+1位置的元素交换，这样我们便完成了一次完整的partition过程，我们记录下此时主元的位置并返回（本例中是4）。

那么我们来回答一下上文提出的一个问题：主元如何选取？其实主元的选取是随机的，数组中任何一个元素都可以成为主元。我们可以调用高级语言提供的一些生成随机数的类库进行选取。而我们只需要让这个主元每次都移动到数组的最右端即可，从而起到“固定主元”的作用。正因为我们能够随机选取主元，所以我们能够实现对数组的随机划分。

那么问题又来了，我们怎么递归执行这个步骤，让整个数组变有序呢？类似于前面归并排序的思想，我们需要将这个数组不断地拆分，不断地让局部“有序化”，那我们以什么作为标准呢？前面执行数组的随机划分过程中，我们记录下了当前主元的位置pivot并返回。没错，我们按照主元的位置对整个数组进行划分，在左右半边递归执行partition。这样我们便实现了将整个数组有序化！

【关键点梳理】

采用分治的思想，利用递归方法，在数组上随机选取主元并以其为基础在数组上执行划分操作。

【代码实现与注释解析】

int Partition(vector<int>& nums,int l,int r){// 对数组nums的[l, r]区间进行划分，并返回pivot的最终位置
    int pivot=nums[r]; //选取数组最右边的元素作为主元
	int i=l-1,j=l;//初始化i,j两指针
	//i用来固定交换位置，j用来遍历数组
	while (j <= r - 1) { // 当j没有遍历到pivot的位置时，继续循环
        if (nums[j] <= pivot) { // 如果当前元素小于等于pivot（小于的放左边）
            i++; // i指针后移，准备交换位置
            swap(nums[i], nums[j]); // 交换nums[i]和nums[j]
        }
        j++; // j指针后移，继续遍历数组
    }
 
    swap(nums[i + 1], nums[r]); // 将pivot换回到它应该在的位置（左半部分的最右边）
    return i + 1; // 返回pivot的位置
}
int RandomPartition(vector<int>& nums,int l,int r){// 随机选取主元，并对数组nums的[l, r]区间进行划分
	int p_idx=rand()%(r-l+1)+l;//在[l,r]上随机取位置，实现主元的随机选取
    swap(nums[r],nums[p_idx]);//将主元换到最右边
    return Partition(nums,l,r);//调用划分函数，实现随机划分
}
void QuickSort(vector<int>& nums,int l,int r){// 使用快速排序算法对数组nums的[l, r]区间进行排序
    if(l>=r){
		return ;
	}
    int p=RandomPartition(nums,l,r);
	 QuickSort(nums, l, p - 1); // 递归对p两侧元素进行排序
     QuickSort(nums, p + 1, r);
}
vector<int> QSort(vector<int>& nums) {// 对数组nums进行快速排序，并返回排序后的数组
        srand(time(0)); // 初始化随机数种子
        QuickSort(nums, 0, nums.size() - 1);
        return nums;
    

和前文所介绍的归并排序算法类似，快速排序也是基于分治和递归实现的，它的时间复杂度为O（nlogn），归因于其原地排序的特性，内部循环的效率和较为简单的实现逻辑，快速排序在大部分情况下比归并排序略快，不过快速排序和归并排序都是效率较高的排序算法。

相信现在回头来看，拿下文章开头的那道leetcode题就很简单了！

以上便是我们今天所介绍的两种效率较高的排序算法，平心而论略有难度，需要结合代码和实例加深理解才能彻底吃透，也希望大家在学习算法的过程中能保持耐心，在不断探索中我们总有一天会突破！我是小高，一名非科班转码的大二学生，水平有限认知浅薄，有不当之处期待批评指正，我们一起成长！