浅谈拓扑排序（C++实现，配合lc经典习题讲解）_c++ 拓扑排序经典题目-优快云博客

【前言】

在实际的有一定规模的项目开发的过程中，我们经常需要编译链接多个文件，如源文件，各种标准库，非标准库等。当项目包含多个文件时，编译器需要根据它们之间的依赖关系来决定编译顺序（比如参考makefile文件）。而这个问题的核心理论依据便是图论算法中的拓扑排序。在看关于拓扑排序算法的介绍之前，需要对图这一数据结构有一定的理解和认识。

【图例讲解】

【有向无环图和AOV网】

首先针对有向无环图这个概念，大家可能会陷入一个误区。比如像下面这张图所画的一样，不难发现这张图在物理结构上是“封闭”的，但是我们需要树立一个观念：环路≠封闭。这里我们应该把存在环路理解为：在图中从某一结点出发，经过若干条路径可以回到这个结点本身，则该图存在环路。同理，若一个在一个有向图中从某一结点出发，经过若干条路径无法回到这个结点本身，则该图就是有向无环图（DAG图）。

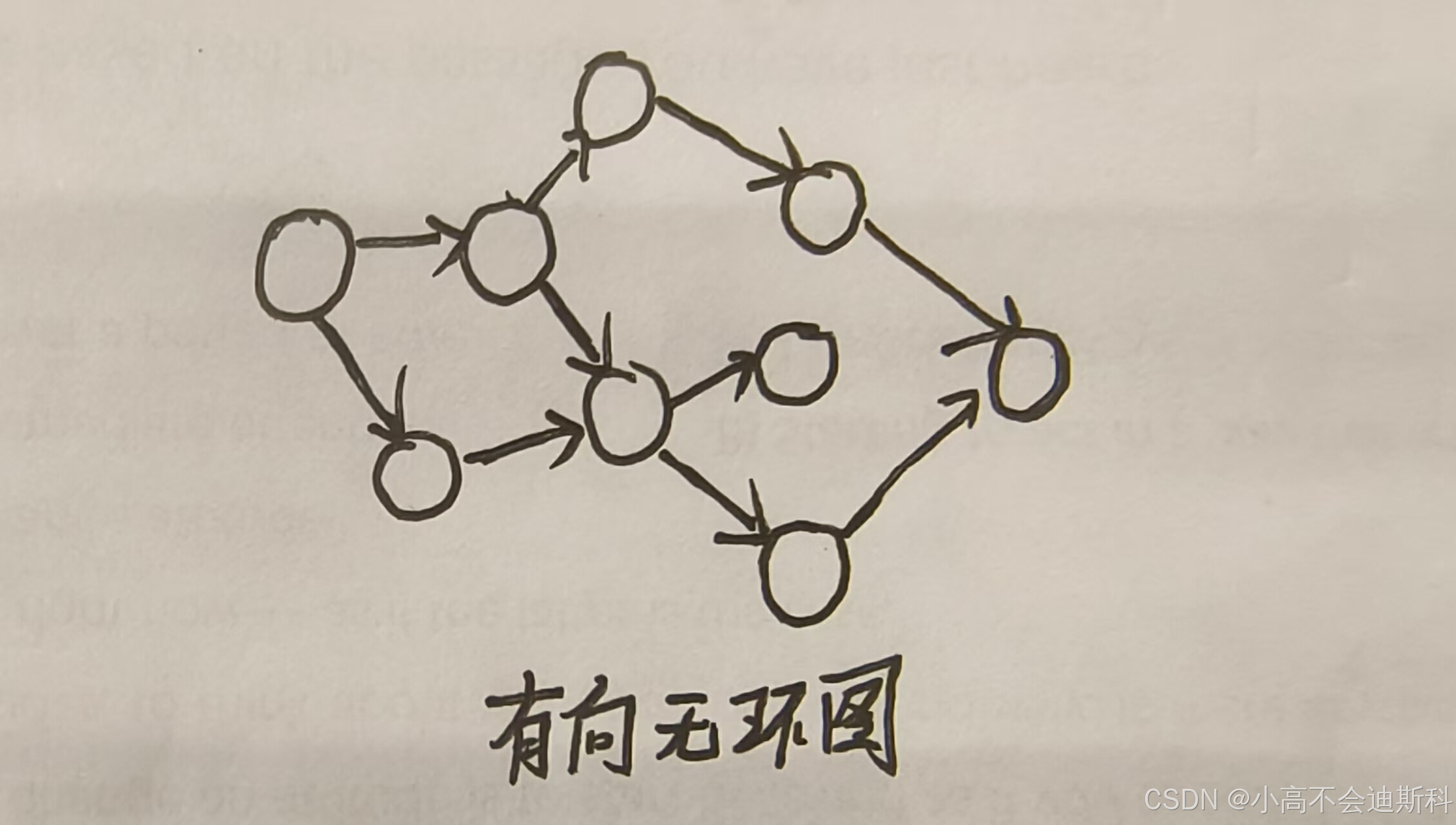
AOV网是在工程建模中常见的一种网络图结构，是有向无环图。其特点是：以顶点表示活动，边表示活动间的依赖关系。在一系列活动当中，如果a->b，即活动a是活动b的先决条件，我们称活动a为活动b的前驱，活动b为活动a的后继。当我们在多维结构中遇到需要将多层依赖关系进行拆解，形成简单的线性依赖关系时，我们往往需要考虑拓扑排序。

【什么是拓扑排序】

拓扑排序是将一个有向无环图（AOV网）中的结点序列化的过程。既然在一个图结构中，存在这么复杂的依赖关系，我们是如何将图中结点所代表的活动进行序列化的呢？我们结合下面图例来进行介绍：

如上图，我们得到了一张有向无环图，现需要对其进行拓扑排序。拓扑排序的大致步骤归结如下：

①先找入度为0的结点

②记录该结点，并擦除该结点及其出度边

③循环执行该步骤

在实际应用场景中，我们常用一张哈希表来存储结点之间的依赖关系。若图中存在多个入度为0的结点，为了将它们依序处理，我们必须对整张图进行遍历。这里我们采用广度优先搜索（BFS）的方式来实现，需要借助队列这一数据结构。所以在拓扑排列算法的大部分使用场景中，我们需要借助哈希表和队列来辅助我们解题。回到上图，在对整张图进行遍历之后，我们得知结点A入度为0。故我们将A记录在拓扑序列中，之后将A和A的出度边擦除，如下图所示（红色虚线实际不存在，此处标明仅方便理解）：

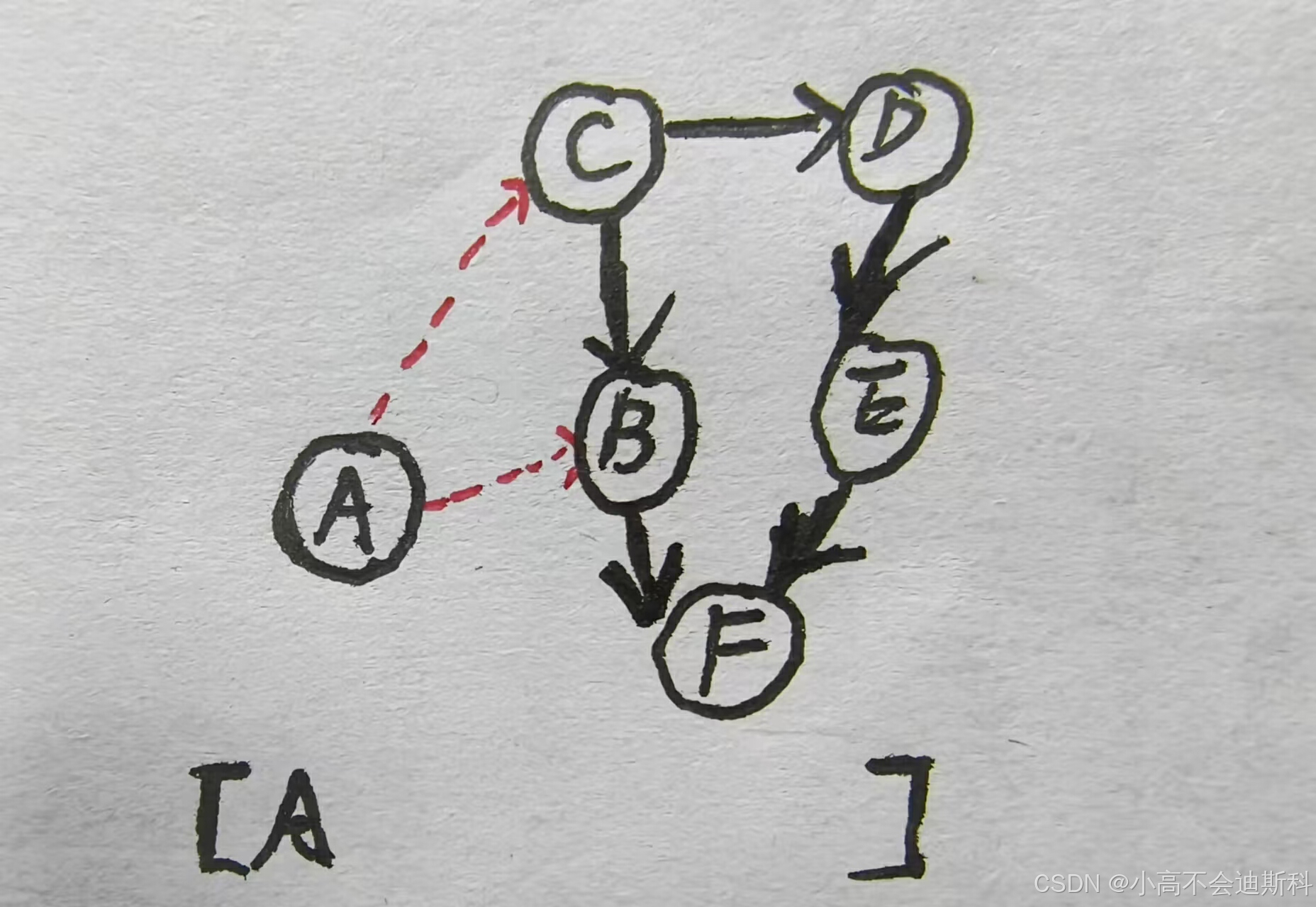
接着遍历整张图，我们得知结点C入度为0。故我们将C记录在拓扑序列中，之后将C和C的出度边擦除，如下图所示：

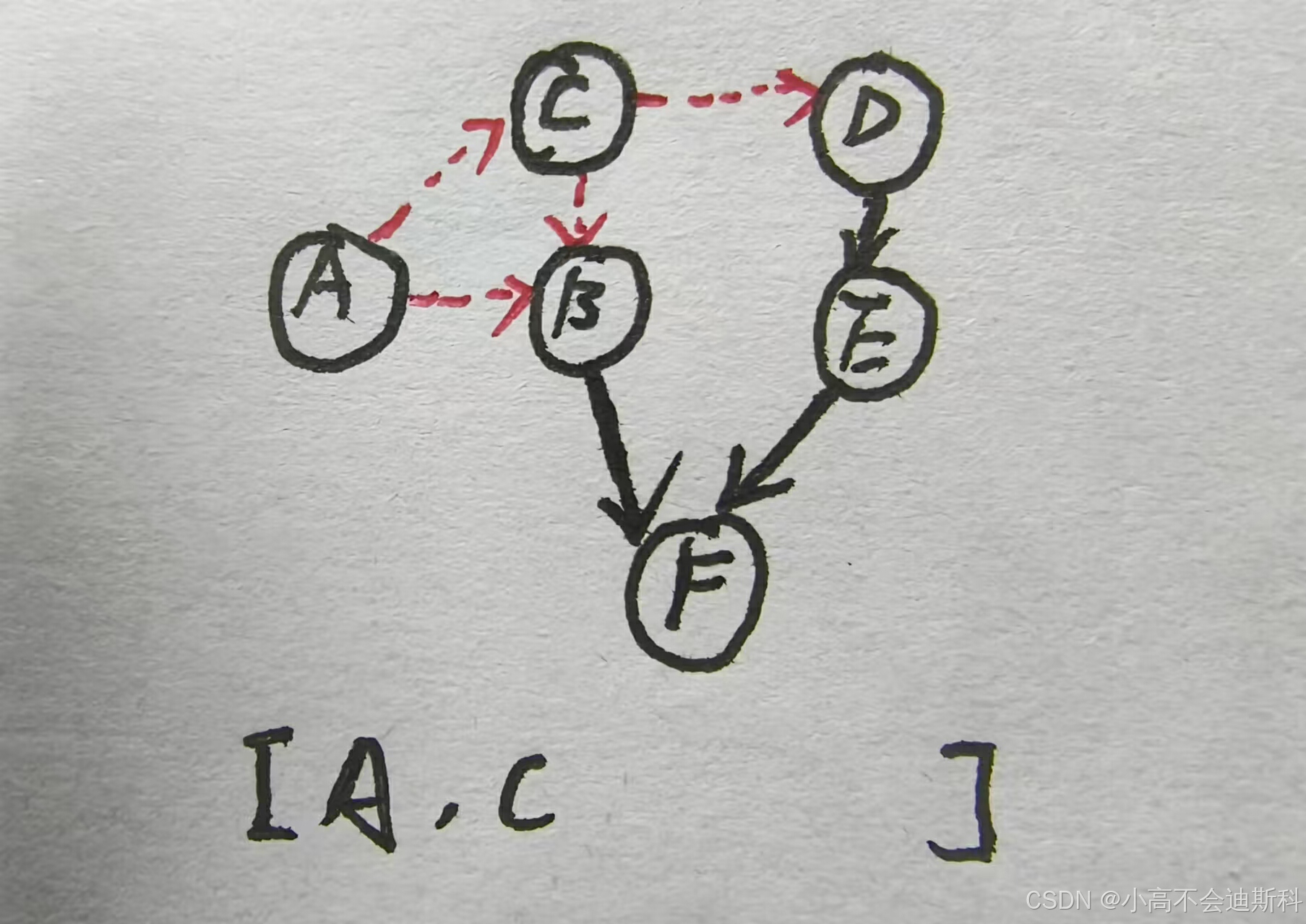
此时我们发现，结点B和结点D的入度均为0，因此我们便将结点B和结点D均入队，之后依序处理。我们假设结点D先入队，故我们将D记录在拓扑序列中，之后将D和D的出度边擦除，如下图所示：

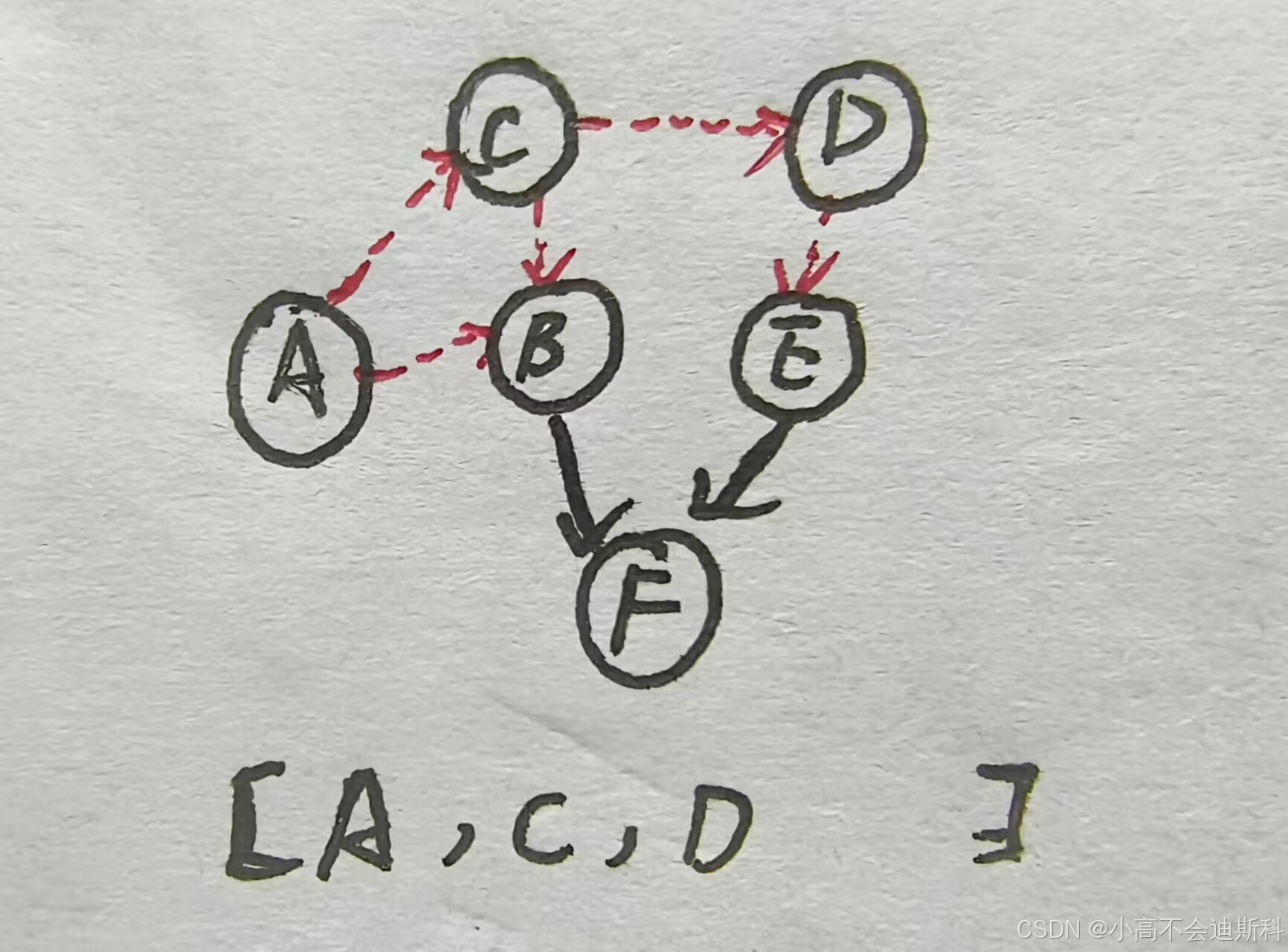
后续步骤与前文同理，因篇幅原因此处不再赘述。由此我们便可得出该图的其中一个拓扑序列{A,C,D,B,E,F}。也正是通过这一过程，我们对图中复杂的依赖关系进行了合理的拆解。由此不难发现：一个有向无环图至少有一组拓扑序列。接下来，我们通过下面leetcode模板题的介绍，来带大家了解拓扑排序算法是如何用代码实现的。

【例题讲解】

模板题--207.课程表-力扣（leetcode)

请大家在看下文的模板代码之前，一定先浏览并理解链接中的题意。在此对上面的题意做一个概括和梳理：假设你现在有n门课要上，编号为0~n-1。数对[0,1]表示你必须先上课程0，再上课程1。如果我们把课程都抽象为结点，那么上面这句话就直接说明了结点之间的依赖关系。这也是我们看到题意后联想到利用拓扑排序进行解题的关键。本题给出了课程名和课程间的依赖关系，问我们是否可以完成所有课程的学习，转换一下就是：将所有课程所代表的结点，根据其依赖关系，建立一张图，对其进行拓扑排序，观察拓扑排序序列是否包含图中的所有结点。如此思路便显而易见了，下面的代码也是拓扑排序题目的模板代码，供给大家做参考。对于拓扑排序，我们只需要写熟大概的结构，然后具体问题具体分析即可：

class Solution {
public:
    bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
        vector<int> inDegree(numCourses);//准备一个vector记录每个节点（课）的入度
        unordered_map<int, vector<int>> map;//准备一个哈希表记录课与课（节点）之间的关系 
        for (int i = 0; i < prerequisites.size(); ++i) {
            inDegree[prerequisites[i][0]]++; //记录入度
            map[prerequisites[i][1]].push_back(prerequisites[i][0]);//记录所有关系
        }
        //定义一个队列，进行BFS广度优先遍历，遍历入度为0的课
        queue<int> q;
        for (int i = 0; i < numCourses; ++i) {
            if (inDegree[i] == 0) q.push(i); //将入度为0的课放入队列
        }
        int cnt = 0;//用于记录有多少门课已经上过了
        //遍历inDegree，更新入度，更新inDegree，直到inDegree的size为0。
        while (!q.empty()) {
            int selected = q.front();
            q.pop();
            cnt++;
            //更新所有关联课程的入度
            for (int i = 0; i < map[selected].size(); ++i) {
                if (inDegree[map[selected][i]] > 0) {
                    inDegree[map[selected][i]]--;
                    if(inDegree[map[selected][i]] == 0) 
                        q.push(map[selected][i]);//将入度降至0的课程放入队列
                }
            }
        }
        //确认cnt是否等于numCourses
        if (cnt == numCourses)
            return true;
        else
            return false;
    }
};

以上便是我对拓扑排序算法的浅薄理解，接下来会连续更新一些图论算法的介绍。图论算法的题目在很多情况下都不会为我们显式建图，所以如何从问题抽象出结点和边，合理建图，是解决所有图论算法问题的关键所在。我是小高，一名非科班转码的大二学生，水平有限认知浅薄，有不当之处期待批评指正，我们一起成长！