浅谈三种O（n^2）的基本排序算法（C++实现）

【前言】

“排序”在算法学习中扮演着一个“引路人”的角色，因为学习排序算法不需要太多数据结构相关的知识，只需要对数组这种线性结构有一定的认识即可。不少朋友由此入坑算法，也有不少朋友由此被“入门即劝退”。在编程实战和算法刷题中，我们经常会对一些数据进行排序处理，以进一步去探寻它们的内在关系和规律。现代很多高级语言都提供了有关排序算法的库函数供我们直接进行调用，也就是说，通过简单的调用，我们可以不关注排序这个过程本身的实现而达到排序的目的。但是排序这个“宽泛”的过程，有各种各样的实现逻辑，这些逻辑中所蕴含的思想甚至能够迁移到其他更复杂的算法中。本文中对nums数组执行不同方式的升序排序。本文中暂不讨论排序的稳定性，后续会有相关文章专门做解释。

【一个小tip】

排序算法为何难？难在哪里？对于我而言，记得刚入门的时候自己也是被复杂的各种变换过程搞得眼花缭乱，抓不到逻辑重点。回过头看，个人认为排序算法捋清变换关系的关键在于：标记追踪。我们不妨把将整个排序的大过程分解为多个移动元素的子过程在循环执行。对某个元素进行标记重点关注，再根据算法逻辑去追踪这个元素的轨迹（只关注其中一个元素即可，用部分来推理总体），可能这样做会更有利于逻辑关系的梳理。

一，选择排序--“抓刺头”

【思路讲解】

所谓“选择排序”，顾名思义关键在于“选择”。那么一个重要的问题来了，选择怎样的元素呢？我们打个比方。老师某次收课后作业来批改，却发现有些人没交，在没有逐一盯对的情况下，老师很可能会认为是班上的某个“刺头”不交作业。没错！在选择排序中，我们选择的元素就是那个“刺头”，那个最耀眼的靓仔！（doge）。在本文中，我们选当前数组的最小值。

那既然把ta选出来了，那总要放在最合适的位置上叭~在升序排列的过程中，最小值一定要放在开头的位置。在这里我们通过操纵下标来间接操纵元素。

首先我们遍历数组，先用一个minIndex作为最小值的索引，初始化为i（可以理解为i位置是一个“分水岭”，i左侧的元素已经有序，i右侧的元素是没有排序的，而已经有序的部分我们只需要原封不动的放着，我们只需要在无序的部分执行“选择”操作），表示我找到的这个“刺头”要放在这个位置。此时假定“局部最小值”是minIndex所指的元素，即nums[minIndex]。

接下来我们从i所指元素的下一个元素（j=i+1）开始遍历数组（不包括i位置的数，这是后续交换步骤的“参照物”），从这个“无序”部分中找到最小值，此时这个“局部最小值”就变成了我们当前找到的最小值（j来到这个最小值所在的位置），将它用minIndex标记（minIndex=j），之后将这个“局部最小值”与“分水岭”处的元素进行交换（swap(nums[i],nums[minIndex])）。

在这之后，已经有一个元素来到了它应该在的位置，此时就不要再动它了，再假设这个元素之后的那个位置为最小值“应该在的位置”，即i位置，循环执行以上过程，直到这个i位置已经到了数组尾端，遍历完毕，证明整个数组都有序了！

【关键点梳理】

每次选择都从未排序部分找到最小（或最大）元素，并放到已排序部分的末尾。

【图例讲解】

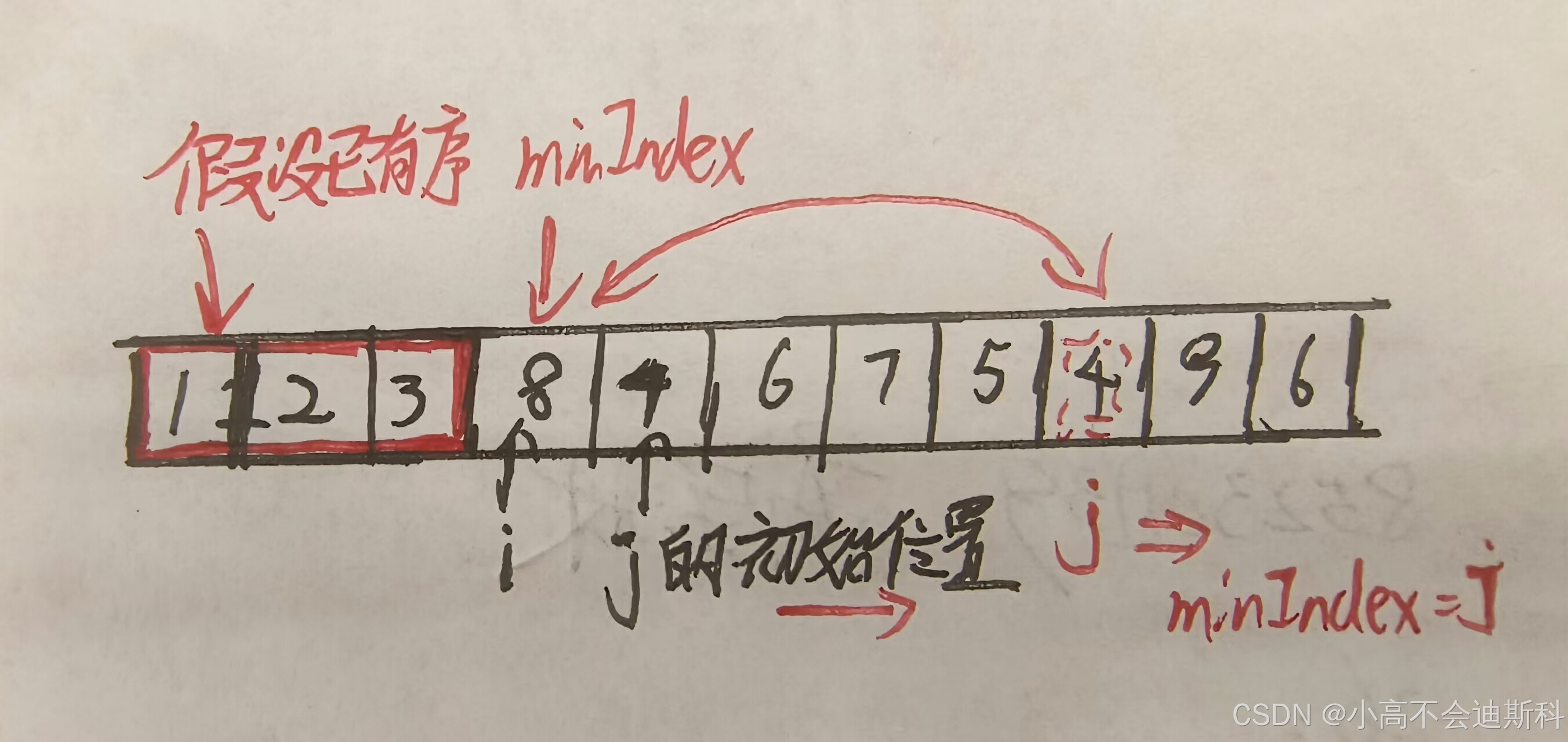我们来看上面给出的图例：假设1，2，3已经有序（红色框框起来的部分），那么minIndex就来到了第四个元素的位置上，也就是对应元素8的这个位置，我们暂定这个8就是最小值。那么我们需要遍历8右边的部分，发现在右边的这个部分中4最小，将其下标标记。之后将8和4进行比较。显然4<8，那么将4,8进行交换，之后{1，2，3，4}便成了一个有序序列，minIndex和i来到了7的位置（minIndex和i一开始是同步的，因为minIndex被初始化为了i），同理循环执行。

【代码实现与注释解析】

void SelectSort(vector<int>& nums) {
	int n = nums.size();//借用数组大小来确定循环范围
	for (int i = 0; i < n; ++i) {
		int minIndex = i;//最小值放在开头的位置
		for (int j = i+1; j < n; ++j) { //内层循环：找最小值
			//我们只需要在还未排好的“子序列”上找这个最小值即可，而不用在整个数组上找
			//j从这个“分水岭”右侧开始即可，即i+1位置
            
            //这个if语句其实就是“选择”二字的体现
            if (nums[j] < nums[minIndex]) {//如果发现了比“分水岭”还小的值
				minIndex = j;//标记为“局部最小值”
                //注意此时的minIndex变动了
			}
			//也可以用三目运算符来写
			//minIndex=(nums[j]<nums[minIndex])?j:minIndex;
		}
		// 将找到的“局部最小值”放到“分水岭”的位置
        // 出现了交换操作
		swap(nums[i], nums[minIndex]);
	}
}

同理，如果我们需要将一个数组降序排列，那么只需要在每次迭代的过程中选择最大值即可，这里不做赘述。

我们在这个实现中使用了嵌套for循环，显然它的最坏时间复杂度为O（n^2)。

由上面代码实现容易看出，最后出现了交换操作，所以选择排序是基于交换的排序。而且这一步交换操作不需要额外的辅助存储空间，也就是说当我们需要限制内存的使用量时，可以考虑选择排序。

二，冒泡排序--“两两比较”

【思路讲解】

前文提到的选择排序，它的子过程是先选择“刺头”，再进行交换，有一种“一步到位”的感觉。而冒泡排序的子过程是每次选中两个相邻元素根据大小关系进行交换，在每一次迭代的过程中执行了多次交换操作，就像水中的泡泡一样，是一点一点冒上去的，而不是“一步到位”。冒泡排序中的交换也给人一种“优胜劣汰”的感觉，就像水中悬浮的物品，轻的会浮上水面，重的便会沉底。

我们拿到了一个无序数组，要为ta进行升序排列，那么在一个元素对（a,b）中，我们需要将二者之中较小的那个让它更靠近数组的首部，较大的那个更靠近数组的尾部。若a<b，这个相对位置和我们的需求是契合的，因此不做操作，而当a>b时便与我们的需求相悖，此时需要将二者进行交换，这便是冒泡排序的子过程。

我们假设数组长度为n，当我们将数组中所有相邻的数进行两两比较，执行交换操作后，到达最右端的数一定是数组中最大的那个数，这便是一次冒泡过程。同理，下一次冒泡过程会将数组中次大的数排在前面找出来的最大的数的左边。我们只需要执行n-1次冒泡排序即可，因为当数组中的其他数字都有序时，唯一剩下的那个数经过迭代交换也一定会在它该在的位置，无需对这个数进行单独操作。

【关键点梳理】

每次遍历都会将未排序部分的最大元素“冒泡”到其正确的位置，“冒泡”过程通过两两交换相邻元素实现。

【图例讲解】

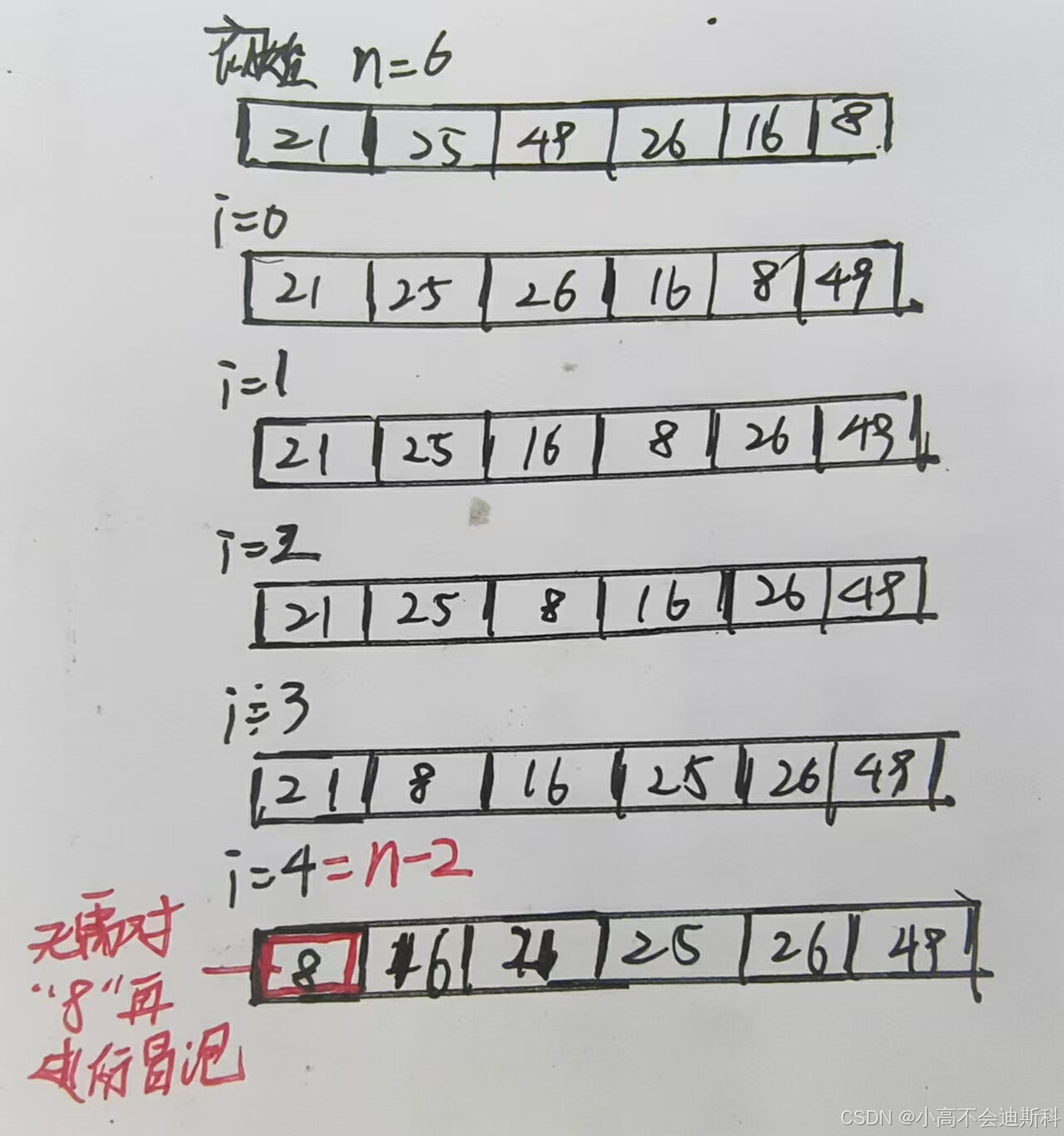
我们来看上面给出的图例：图中给出了一个长度为6的无序数组，我们只需要执行5次冒泡过程。第一趟对初始数组的相邻元素两两交换，则49会来到数组的最右端。后面几趟同理，每一趟的交换结果图中都有展示。当执行到第四趟时，显然，8已经在它该在的位置上了，即最小值的位置，我们无需对8进行处理。

【代码实现与注释解析】

void BubbleSort(vector<int>& nums) {
	int n = nums.size();
    //外层for循环，代表执行n-1次的冒泡过程
	for (int i = 0; i < n-2; ++i) {
        //内层for循环描述冒泡过程
		for (int j = 0; j != n-1; ++j) {
            //当发现前者大于后者
			if (nums[j] > nums[j+1]) {
				swap(nums[j], nums[j+1]);
                //这里推广一种交换方法：异或运算
                //nums[j]=nums[j]^nums[j+1];
                //nums[j+1]=nums[j+1]^nums[j];
                //nums[j]=nums[j]^nums[j+1];
			}
		}
	}
}

我们在这个实现中使用了嵌套for循环，显然它的最坏时间复杂度为O（n^2)。当数据量很大的时候，考虑到执行交换操作的时间成本，故不适合使用冒泡排序。

【易错点-数组下标越界】

在写冒泡排序的过程中，初学者最容易犯的错误就是不注意下标的使用细节，导致数组下标越界，从而引发中断进入异常处理程序。在上面的代码中，(nums[j],nums[j+1])是两个相邻的元素，我们对它们执行相关操作，但是为什么不能是(nums[j-1],nums[j])这两个相邻元素呢？观察内层的循环条件可知，j变量被初始化为0，但是当j=0时，j-1对应的下标成了-1！由此引发了数组下标的越界。所以在线性结构上执行增删改查循环用到下标操作时，我们一定要根据初始条件来确定下标，确保其满足条件，不会产生未定义的行为。

【优化】

实际上，我们可能遇到这样的情况。在执行到第n-1趟之前，我们的数组就已经全部有序了。也就是说，对前面这些数再进行遍历行为会导致浪费。所以我们给出如下优化方案来最大限度地减少浪费：在遍历数组的过程中，由上面的逻辑，可以确定只要存在“无序”的部分一定会产生交换行为。我们设置一个布尔变量来标记是否产生了交换行为。如果产生交换行为标记为true默认执行下去，如果不产生交换行为说明整个数组已经有序，则无序进行后面的遍历工作，标记为false并退出。

void GreaterBubbleSort(vector<int>& nums) {
    int n = nums.size();
    for (int i = 0; i < n - 2; ++i) { 
        bool isSwapped = false; // 标记是否发生了交换
        for (int j = 0; j < n-1; ++j) { 
            if (nums[j] > nums[j+1]) {
                swap(nums[j], nums[j+1]);
                swapped = true; // 标记发生了交换
            }
        }
        if (!isSwapped) {
            break; // 如果没有发生交换，说明数组已经排序完成，提前退出
        }
    }
}

由此不难看出，当整个数组基本有序时，使用冒泡排序的这种优化算法是效率较高的。

三，插入排序--“能人上位”

【思路讲解】

在前文介绍过的选择排序中，我们选出整个数组中的“刺头”，之后通过“与目标位置的元素交换”达到使局部有序的目的，而在插入排序中，我们将整个数组分为未排序和已排序两个子序列。对于未排序子序列上面的这些元素，我们在已排序子序列上从后往前进行遍历，通过比较行为来搜索插入位置。通过让插入位置之后其他元素移动位置腾出空位（假设找到的插入位置为j，那么执行nums[j+1]=nums[j],通过元素后移腾出j位置）来实现局部有序，从而通过循环执行该过程实现整体有序。那么问题来了，我们怎样来确定我们要将哪个元素进行插入操作呢（后文用待插入元素来描述）？

我们拿到了一个无序数组，这里我们将首元素与其他元素隔离，由此不难看出，“首元素”所代表的部分是有序的（不严谨地讲，单个元素一定是有序的）。那么我们将第二个元素作为“待插入元素”（我们用x对其进行标记）。没错！“待插入元素”所在的位置就是一个“分水岭”，也可以看作一个“能人”！在这个元素左侧是有序子序列，而在它的右侧则是无序子序列，且左侧的“有序子序列”不能为空，否则搜索插入位置的操作就无从谈起，这也就是我们将“待插入元素”的位置定在第二个元素的原因所在。接着执行上文所提到的步骤，执行搜索，其他元素腾位置（有点像一个公司中来了一个能力很强的人来代替某个人的位置，那ta就得乖乖让位），执行插入操作，维持有序子序列的有序性。之后这个“待插入元素”移动到第三个元素的位置上，依此类推循环执行，直到有序子序列覆盖了全部数组，则说明整体有序，排序结束！

【关键点梳理】

通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入,会有通过移动元素来腾出插入位置的行为，必须将“待插入元素”用一个变量标记，否则当进行元素移动操作时该元素会被覆盖。

【图例讲解】

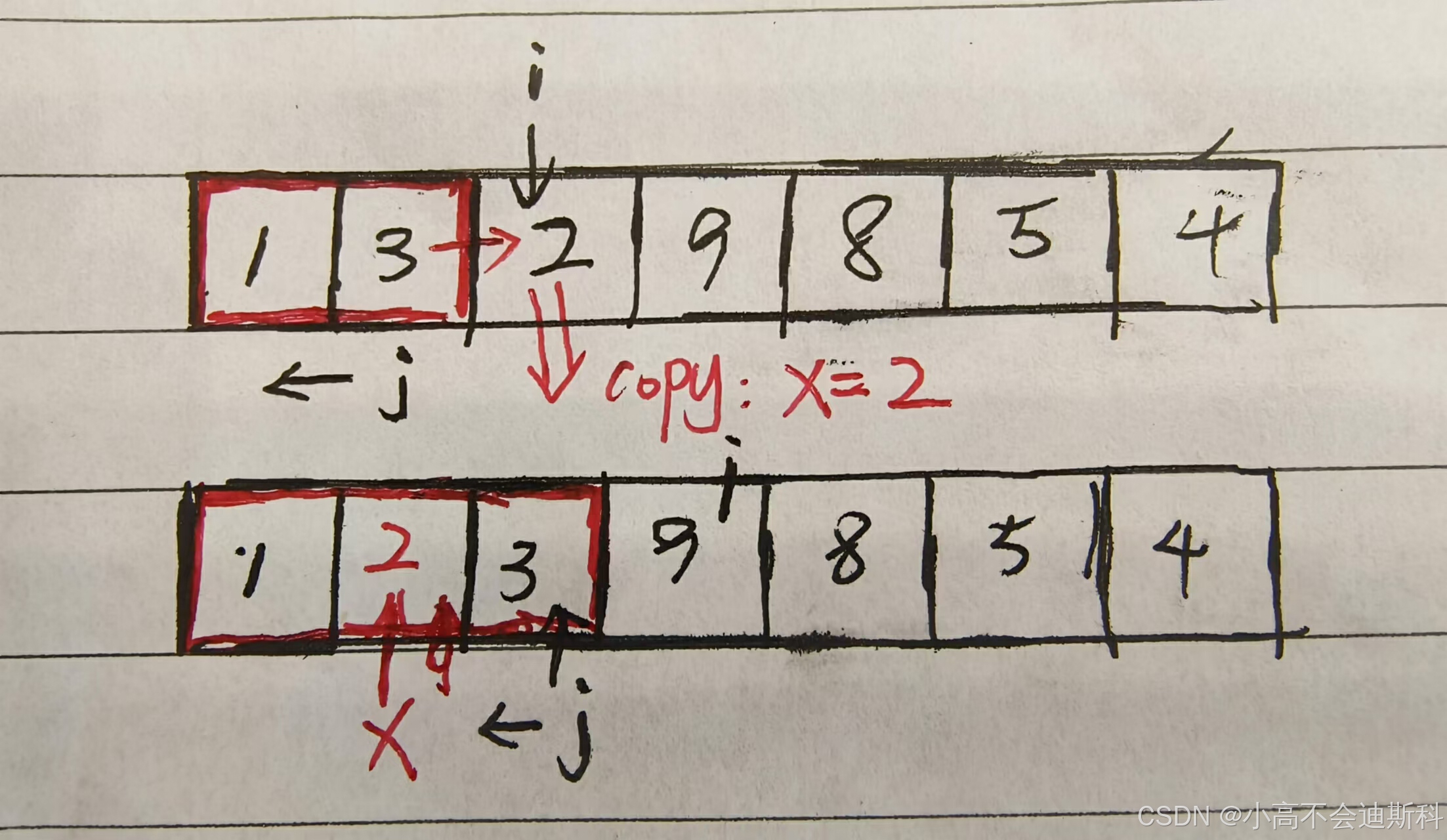
我们来看上面给出的图例：假设{1,3}构成了有序子序列，那么我们便把无序子序列的首元素（即2）看作“待插入的元素”并用x标记，接着在红色框框起来的部分寻找“2”的插入位置，不难发现应该插在3的前面。此时我们便将元素“3”向右移动一位（效果是覆盖了2所在的位置），但是我们提前已经用变量x存储了这个“2”，就可以以x变量为媒介执行插入操作。在这之后{1,2,3}构成有序子序列，无序子序列的首元素为“9”，继续将其标记，循环执行直到整个数组有序。

【代码实现与注释解析】

//直接插入排序
void InsertSort(vector<int>& nums) {
	int n = nums.size();
	for (int i = 1; i < n; ++i) { // 从第二个元素开始，因为第一个元素前面没有元素需要比较
		int x = nums[i];//复制插入元素
		int j = i - 1;//从“待插入元素”的左边开始搜索
        //搜索插入位置，从右向左
		while (j >= 0 && nums[j] > x) {
            //元素后移，腾出插入位置
			nums[j + 1] = nums[j];
			--j;
		}
		nums[j + 1] = x; // 将 x 插入到正确的位置
	}
}

【优化-二分插入排序】

由前文不难看出，我们需要在有序的部分查找元素的插入位置。而前文所提到的顺序遍历数组的方法，属于“线性枚举”的思想，时间复杂度为O(n)。我们可以采用二分查找的策略来优化搜索过程的时间复杂度（O（nlogn）），这种方法也称为“二分插入排序”。因涉及到二分算法的思想，后续文章会进行专题讲解，篇幅有限，本文暂不涉及，在此先引出二分插入排序的代码实现。

void BinaryInsertionSort(vector<int>& nums) {
    int n = nums.size();
    for (int i = 1; i < n; ++i) {
        int x = nums[i];
        int left = 0, right = i - 1;
        int pos = -1; //用pos存储x应该插入的位置
 
        // 使用二分查找找到x的插入位置
        while (left <= right) {
            int mid = left + (right - left) / 2;
            if (nums[mid] <= x) {
                left = mid + 1;
                pos = left; // 更新pos为当前mid的下一个位置
            } else {
                right = mid - 1;
            }
        }
        // 注意：这里的pos实际上是在“腾出空间后”x应该占据的位置
        
 
        // 移动元素以腾出空间
        for (int j = i - 1; j >= pos; --j) {
            nums[j + 1] = nums[j];
        }
 
        // 插入x
        nums[pos] = x;
    }
}

【总结】

基于上文的讲述，O（n^2）的排序之所以性能较差是因为浪费了大量的比较行为，后续我们会介绍一系列性能更优的排序算法。

我是小高，一名非科班转码的大二学生。认知浅薄，有不当之处希望大家多多批评指正，我们一起成长！