经过了一段时间的迷茫期,最终我还是回来了。我只是一个极其普通的后端开发学习者,能力有限,在这里记录自己曾经的所见所学,如果有幸也更想帮助到志同道合的朋友们。书不尽言,词不达意,日后时间充裕我会在自己喜欢的领域保持内容的更新。本文大概梳理一下递归算法是如何慢慢演进为动态规划的,以及我们会举出一些经典的题目进行分析。动态规划算法广且深,不仅限于维度,还会有背包dp,树形dp,区间dp,状压dp,数位dp等等,以及各种时间,空间层面的优化,这些内容后续会陆续更新,也请感兴趣的朋友们持续关注。同时声明,这篇文章也是我通过学习左程云老师课程笔记的一个复现,旨在进行记录。基于个人刷题习惯,还是采用C++来进行代码的演示,不过在算法学习中语言并没有本质区别。
相信有不少朋友曾经和我一样,被动态规划所谓的“重叠子问题”,“最优子结构”给劝退,看着高深的“天书”而望洋兴叹。此时不妨换个思路,何必钻这些术语的牛角尖呢?我们不如来实际看一道简单但有代表性的题目,在解决问题的过程中看看能不能给我们带来一些灵感,找到一些共性。
题目描述请看链接,相信有一定算法基础的朋友一定对这道题不陌生,甚至一眼能秒出答案。但是我想说,做题不是主要目的,我们要从简单的题目中有所发现,要知道一道题目为什么简单,为什么难。用一道简单的题目能够最直观的发现一些基本的结论。
题目描述中更是直接给出了斐波那契数的计算公式
F(0) = 0,F(1) = 1 F(n) = F(n - 1) + F(n - 2),其中 n > 1
我们很容易就能根据上面的这个公式写出如下的程序:
class Solution {
public:
int F(int n) {
if(n<=1){
return n;
}
return F(n-1)+F(n-2);
}
};这段程序在实现上看似没有任何难度,但是朋友们你们知道这段程序在计算机中是如何执行的吗?如果有一定硬件基础或者懂汇编语言的朋友一定不会陌生,在计算机的内存当中,递归函数是由内存栈区当中的函数调用栈来进行管理的,这个内存区域存储的是函数调用的上下文,由编译器执行自动管理,在函数执行结束后释放该内存区域。之前我们在讲解单调栈专题的时候也对栈这个LIFO特性的数据结构作了介绍。
结合斐波那契数的公式来看,假设当前需要计算F[i]的值,那么F[i]的取值依赖于F[i-1]和F[i-2]的取值。我们举实例来描述这个过程,比如我们跟踪一下F[4]的执行过程,请看下图:
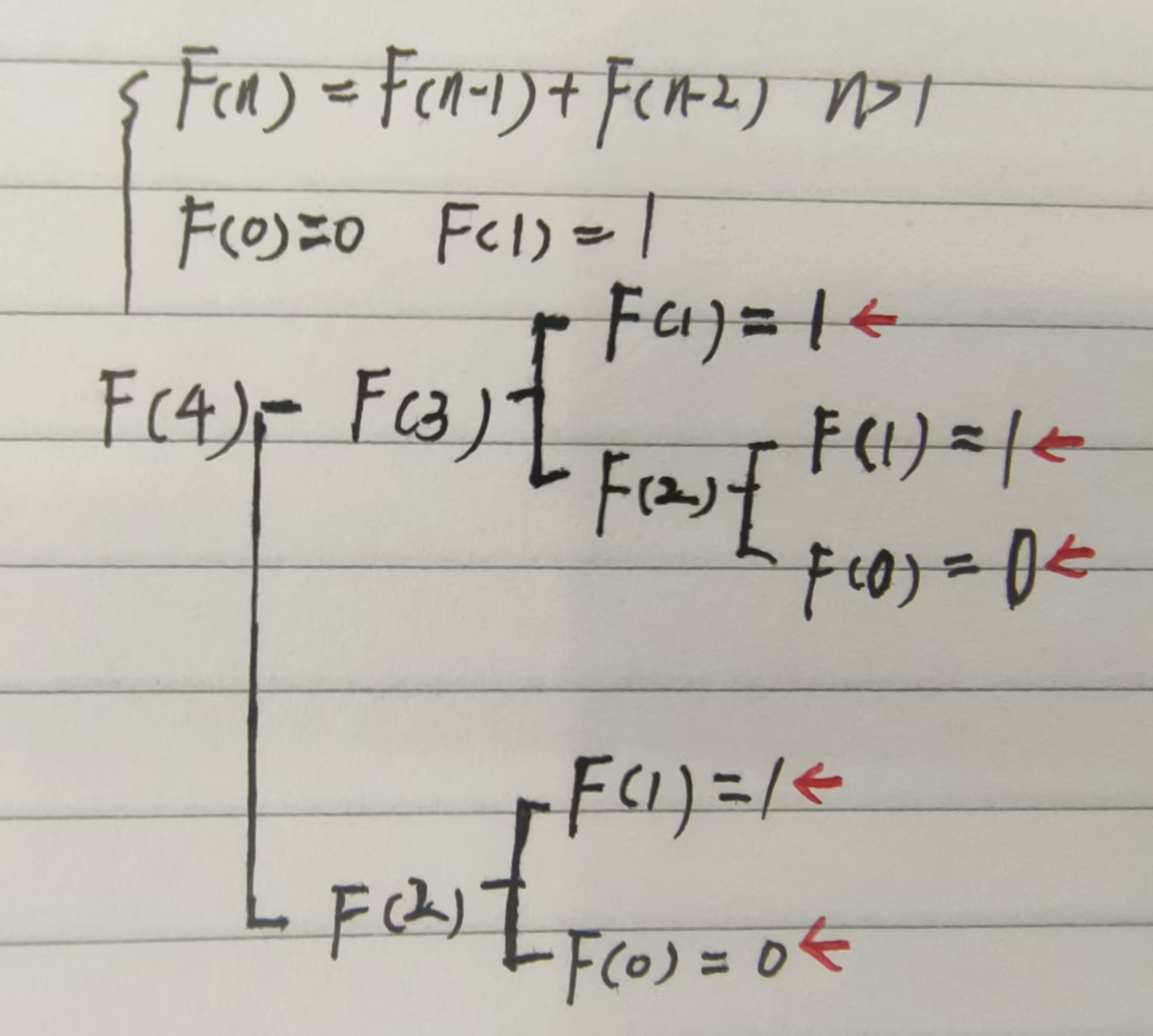
整理之后我们不难发现这种依赖关系是呈树型的,在这里朋友们会不会发现一个特性:在调用F(4)的时候,其实它也不知道F(3)和F(2)的值到底是什么,F(3)也是一样,只有当分解到F(1),F(0)的时候,发现它们的值是被给定的,一切豁然开朗。我们称F(1),F(0)为递归出口。接下来我们所有的数,诸如F(2),F(3),F(4)也正是由这个递归出口的值计算得来的。这看似就是一个“先向下拆解,后整合返回”。而这个过程很符合栈这个数据结构处理数据的特征。在这个例子中在没有得到F(1),F(0)递归出口的值之前,我们只管把F(4),F(3),F(2)统统压栈,得到递归出口后求值之后出栈即可。如果到目前你都能理解,那么恭喜你已经大概掌握了递归的基本原理。而递归题目最难的点,就在于如何写出递推公式。这个问题延申到动态规划问题上就是如何写出状态转移方程。不过本质上是一样的,那就是如何整理出最优尝试。
接下来我们也不可避免的要分析一下使用递归方法解决的问题。首先我们要了解,在计算机内存资源中,栈空间通常是比较小的。比如在斐波那契数问题中,你如果要求个F(8亿),那怕是直接就"爆栈"了,也就是我们常说的由于递归深度太深,导致的栈溢出,传统递归方法的时间复杂度可是指数级的!那么接下来问题的关键就是我们能不能减少压栈次数呢?我们还是看上面递归过程的树状图,不难发现,在这个递归过程中F(2),F(1),F(0)通通被压栈了不止一次,实际上这种重复的压栈是多余的!我们可以用一张表mem来记录当前求得函数结果的值,当有上一级函数需要这个数值的时候,我们无需压栈处理,而是直接返回!由此就引出了第一种递归的优化方式:记忆化搜索,演示代码如下:
class Solution {
public:
int F(int n, vector<int>& mem) {
if (mem[n] != -1) {
return mem[n];
}
mem[n] = F(n - 1, mem) + F(n - 2, mem);
return mem[n];
}
int fib(int n) {
if (n < 0) return -1;
if (n == 0) return 0;
vector<int> mem(n + 1, -1);
mem[0] = 0;
mem[1] = 1;
return F(n, mem);
}
};记忆化搜索本质上仍然是递归的方式解决问题,但是效率大幅提升,有效避免了重复计算,时间复杂度优化到了O(n)水平,但是同时也引入了O(n)的空间开销。由记忆化搜索我们不难获取到一点灵感,既然我们通过引入表结构来降低计算时的查询成本,那我们莫不如把依赖关系直接整理到一张表结构中呢!这又何乐而不为呢?我们不再依赖递归的方式,而是采用循环进行迭代。这可以有效地解决递归深度过大爆栈的问题。这就是一维动态规划的本质了!如果还没理解,没关系,请看下面这张图:

我们把依赖关系整理到上面这张dp表中,以目标值n作为下标,数组中存储的是计算得出的斐波那契数值,由题目条件我们不难得出dp[0]=0,dp[1]=1这种特殊位置处的初始条件,以及在非特殊位置i处都有dp[i]=dp[i-1]+dp[i-2]这个状态转移方程。仔细观察其实不难发现,这个状态转移方程和递推公式本质上没有太大区别,这道题简单就简单在把递推公式(尝试模型)直接给出来了!而真正意义上的难题的难度在于需要自己根据题目描述整理最优的尝试模型,并且确定边界。接着我们继续来看这张表,我们不难发现这张表是由传进来的参数n来进行组织的。在一般情况下,动态规划问题中传入可变参数的数量决定了动态规划的维数。所以这道题目属于一维动态规划,下面来看演示代码:
class Solution {
public:
int fib(int n) {
if(n<=1){
return n;
}
vector<int>dp (n+1);
//初始条件
dp[0]=0;
dp[1]=1;
//循环迭代,填写dp表
for(int i=2;i<=n;i++){
dp[i]=dp[i-1]+dp[i-2];
}
return dp[n];
}
};这时候可能有朋友难免又有疑问了:我这一通优化猛如虎,结果一看就是削减了递归过程中的栈空间开销,时间复杂度和空间复杂度还是O(n)水平啊!别急,饭不能一口吞,能从递归转化到动态规划已经是很大的一步了。但是如果说还能不能优化呢,答案是,能!由于我们填写dp表需要迭代更新,时间复杂度方面没有太大的优化空间,这个时候我们换个思路,去优化空间。我们来想一个比较实际的场景,假如说你要求第10000个斐波那契数(不考虑求之前数的过程),根据尝试模型,你只需要第9999和第9998个斐波那契数,但是实际上,你并不需要第9998个以前的所有斐波那契数,而这些数字还存在dp表中,岂不是对空间的浪费吗?我们就拿这些之前被用过,现在已无用的数字来开刀。我们来看下面这张图:
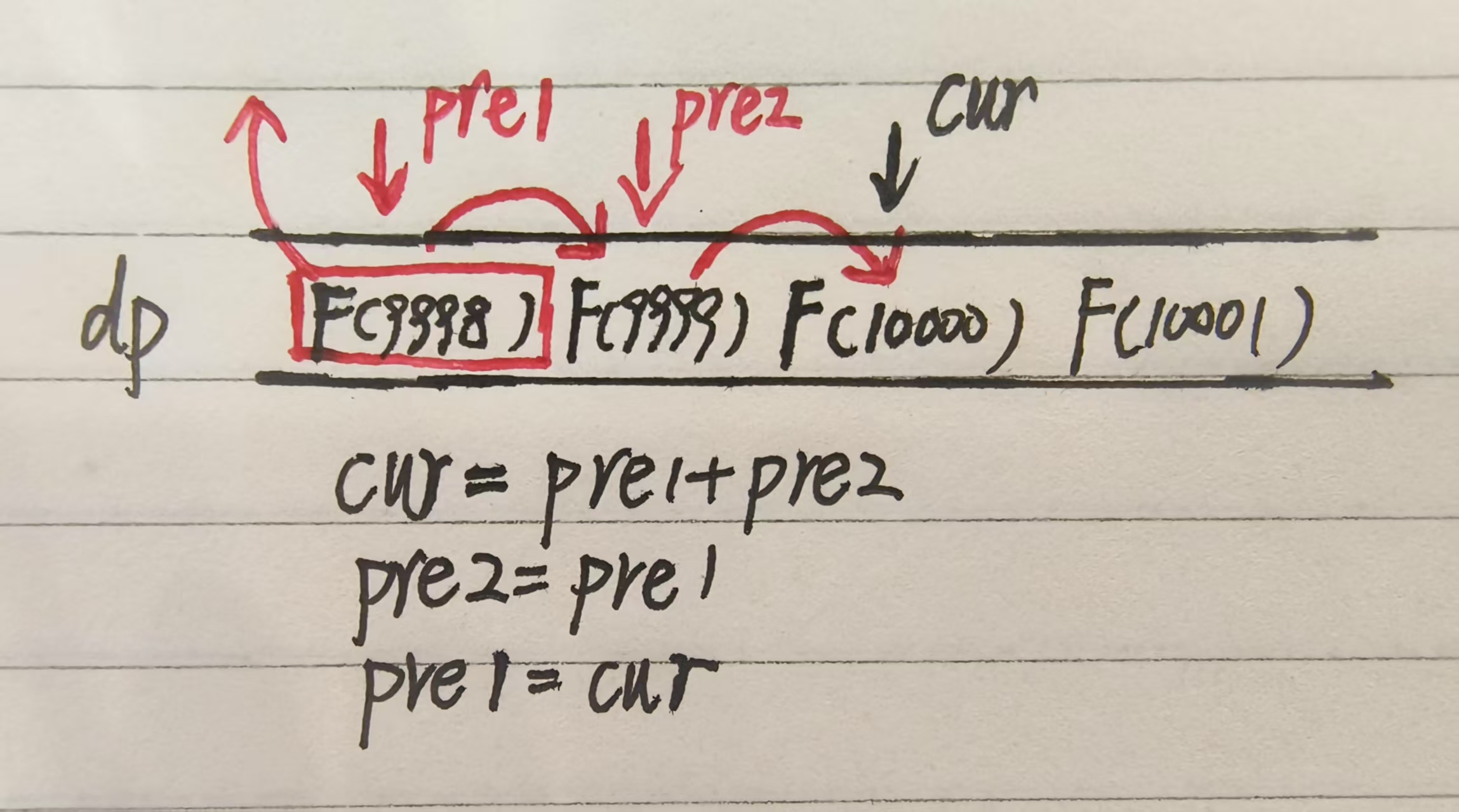
这里我们仍然用F(i)来表示第i个斐波那契数。假设我们需要计算F(10000),那么在计算完F(10000)的值之后,如果要计算F(10001)的值,F(9998)的值就不再需要了!由之前列出的状态转移方程我们不难看出求当前位置的值的时候我们需要前两个位置的依赖。我们用两个变量(我的建议是这里最好不要理解成指针,这个过程并不是指针的移动,而是值的复制)pre1(初始化为F(0)),pre2(初始化为F(1))来标记这两个依赖位置,不难发现当前位置的斐波那契数值可以由pre1+pre2直接获得。之后通过值的复制,实际产生的效果是让F(9999)成为pre1,让F(10000)成为pre2,此时F(9998)没有被任何变量标记,可以理解为从这个dp数组中被踢出去了!最后再由现在的pre1+pre2计算出当前cur(F(10001))的值,如此循环往复。不难发现这个数组从始至终只有三个值,里面的数字好像在滚动,有的出去有的进来,甚至因为数组中元素有限我们不需要额外建表了,我们称这种优化方式为“滚动数组”优化。滚动数组中有多少元素取决于依赖位置的个数。由此,我们的空间复杂度就被丝滑优化到了常数级别。滚动数组设置的意义就是让dp数组不实际存在!比起传统的递归方式提升很大!接下来看演示代码:
class Solution {
public:
int fib(int n) {
if(n<=1){
return n;
}
//设置标记变量
int pre2=0,pre1=1,cur;
//迭代更新
for(int i=2;i<=n;i++){
cur=pre1+pre2;
pre2=pre1;
pre1=cur;
}
return cur;
}
};好的,以上就是本文的全部内容了。总结来说,递归->记忆化搜索->动态规划->滚动数组优化,无论哪个环节,最难的核心点都是如何写出最好的尝试模型。不得不承认,这与刷题量和题感有直接关系,也只能多练多积累。接下来的文章也会着重从这个角度进行切入,引入好题,难题实战演练,还请大家多多关注和支持,我们一起成长!





















 1745
1745

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








