学习日历day06 动态规划01背包问题（笔记）

推荐大家可以去看b站邋遢大哥223的[轻松掌握动态规划]4.01背包，以下为学习后的相关笔记

01背包问题：

你需要从一系列物品中选择一部分物品放入背包。但是，你的背包容量有限，假设背包容量是8，你只能装下重量（weight）和小于等于8的物品。每件物品都有两个属性：重量（weight）和价值（value）。目标是在不超过背包最大承重的前提下，选择物品使得总价值最大。

通常，我们可能会想，选择性价比较高的物品装入背包（性价比=value/weight），但是往往实际情况并非装性价比最高物品就能得到最优解。

比如：物品a：重量为5，价值为10；

物品b：重量为4，价值为5；

物品c：重量为4，价值为6

如果我们选择性价比最优的，应为物品a，但是装入物品a后的价值明显小于装入物品c与b的价值，且装入物品a造成3个重量空间的浪费。

如果用暴力求解算法，即逐一计算，由于每件商品都可以选择放与不放，假设有n件商品，那么此时就有2的n次方中计算数据，时间复杂度过高。因而接下来探讨如何用动态规划解决01背包问题。

动态规划解决01背包问题

定义一个二维数组D[i][j]，求放前i件商品在容量为j的背包，怎么样才能让背包放下的商品价值最大。

比如D[4][8]表示求前四件商品abcd放入背包容量为8的背包，怎么放商品才能实现价值最大化。

左边关于abcd的参数表格说明了商品的价值与重量。

求D[4][8]时，有两种情况：

情况一：第四件商品d不放，那么此时最大价值继承与前三件商品放置的最大价值，即D[4][8]的最大价值为D[3][8]的最大价值

情况二：第四件商品d放置，商品总价值为d的价值6加上8-5=3容量的背包可以放的最大价值D[3][3].公式为D[i][j]=value[i-1]+D[i-1][j-weight[i-1]]。注意！这里的i-1指的都是第i件商品，由于数组下标从0开始，而D[i][j]值得第i件商品。

D[i][j]根据以上两种情况中得到的值取一个大的，便可得到D[i][j]的最大价值

子问题：

D[0][0]=0：容量为0的背包放0个商品，最大价值为0；

D[i][0]=0：容量为0的背包放i个商品，最大价值为0；

D[0][j]=0：容量为j的背包放0个商品，最大价值为0；

根据分析，将上述价值填入以下表格

表格里的数字表示D[i][j]的相关价值，纵坐标表示放入前几件物品（有范围限制，只能在前几件物品里选择是否放置），横坐标表示背包容量。左侧为物品abcd对应的重量和价值。？为需要求的数字

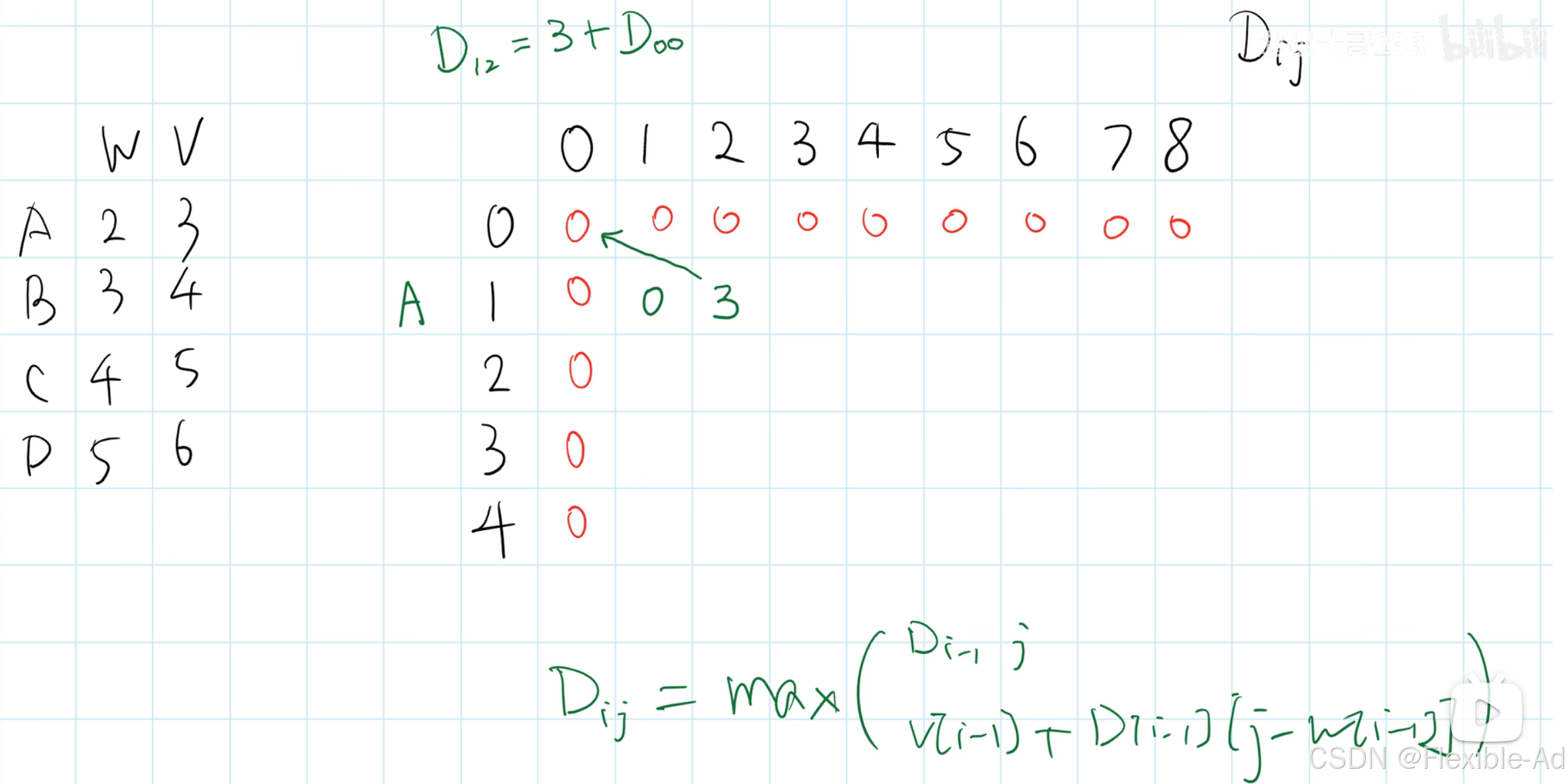
以D[1][2]为例，先比较a的weight是否可以放入，a的重量比背包容量大时，说明该物品不能放入，直接看上一行，将正上方上一行的数值写入。a的重量比背包容量小时，如果不放入a商品，看D[0][2]，为0；放入a商品，看即D[1-1=0][2-2=0],为0，加上3，得D[1][2]为3.相比较，D[1][2]取3。

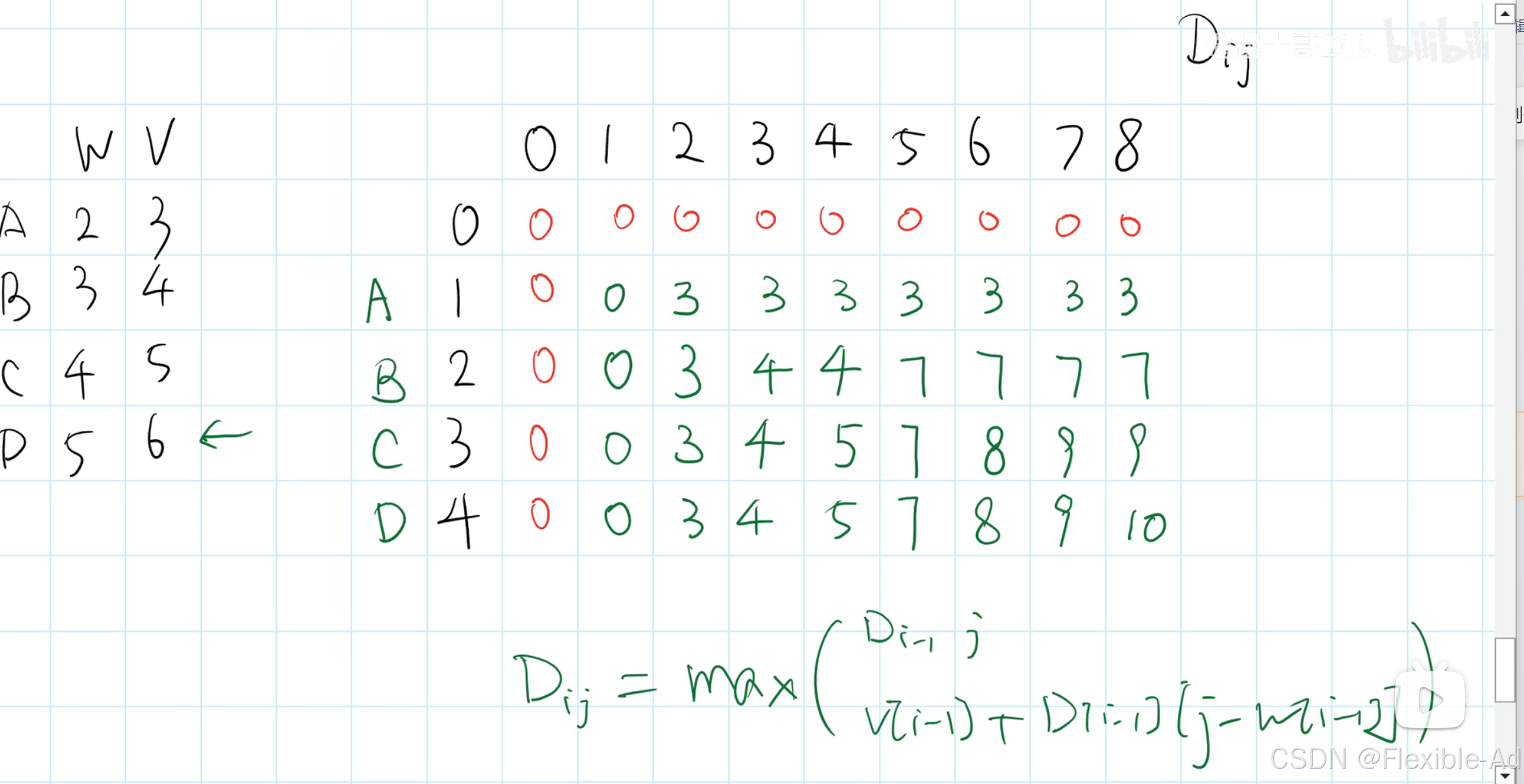
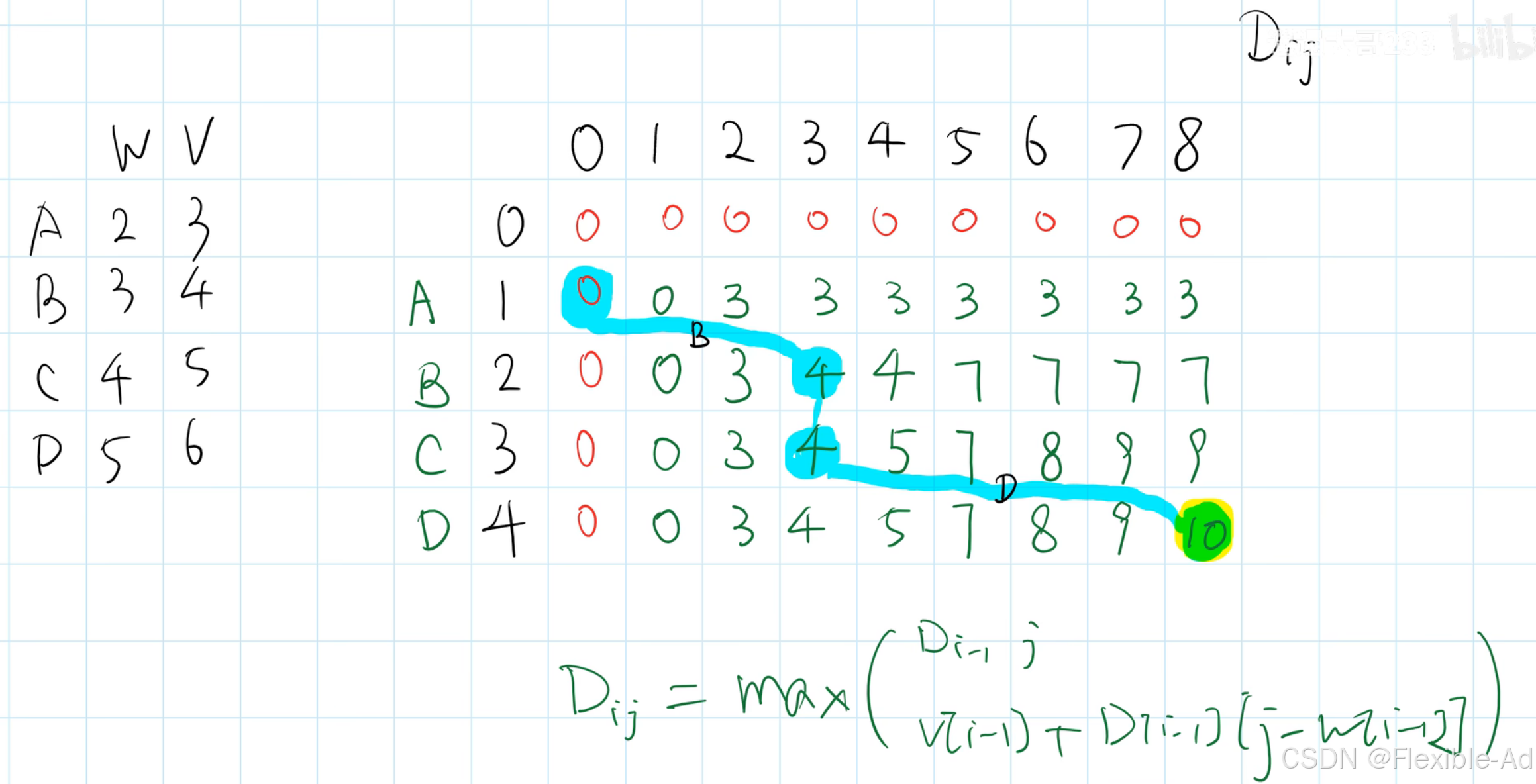
伪代码 

 

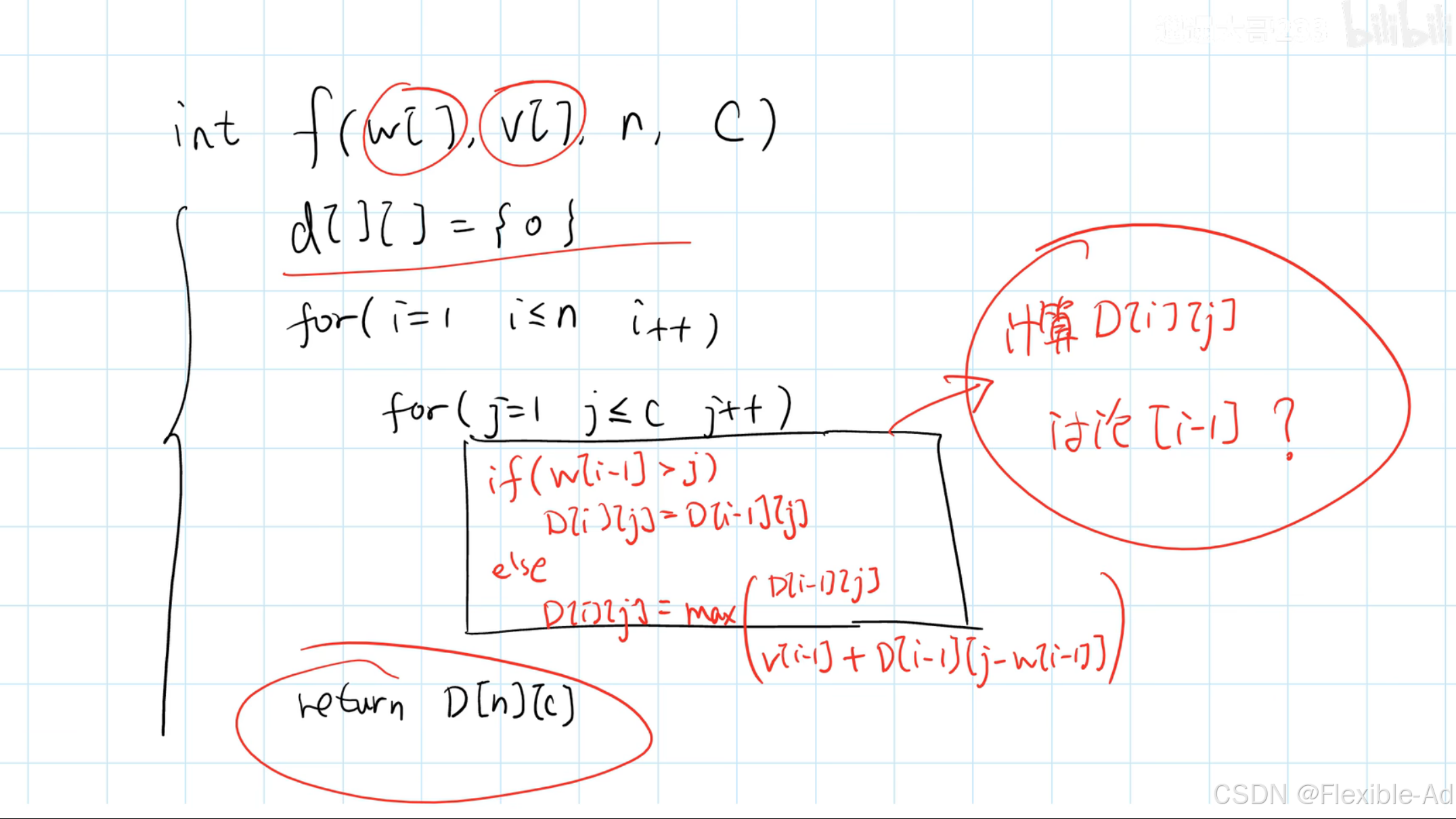
代码实现

def knapsack(weights, values, capacity):
    n=len(weights)
    #创建一个二维数组dp，行代表第几个物品，列代表背包容量
    #初始化dp,把所有元素置为0
    dp=[[0 for i in range(capacity+1)]for j in range(n+1)]
    #填充dp数组
    for i in range(1,n+1):
        for j in range(1,capacity+1):
            if weights[i-1]>j:# 如果当前物品不能放入背包，则不放入
                dp[i][j]=dp[i-1][j]
            else:
                num1=dp[i-1][j]
                num2=values[i-1]+dp[i-1][j-weights[i-1]]
                dp[i][j]=max(num1,num2)
    return dp[n][capacity]
weights = [2, 3, 4, 5]
values = [3, 4, 5, 6]
capacity = 10
# 调用函数并打印结果
max_value = knapsack(weights, values, capacity)
print("最大价值:", max_value)