学习日历day08 动态规划-最优二叉搜索树

例子引入

：比如你需要查找某个单词，大数据会将查找频率高（此处查找频率对应权值Wi）的单词优先展示，放在根节点位置，使用户能用更少的检索快速查到单词

最优二叉树问题

以下为最优二叉树问题的输入输出

假设有两个结点1，2。对应权值为W1W2，那么，有两种排序方式，如下图，计算公式为：该结点权值×（结点深度＋1）。然后取两种情况中的较小值，便是我们要求的数。

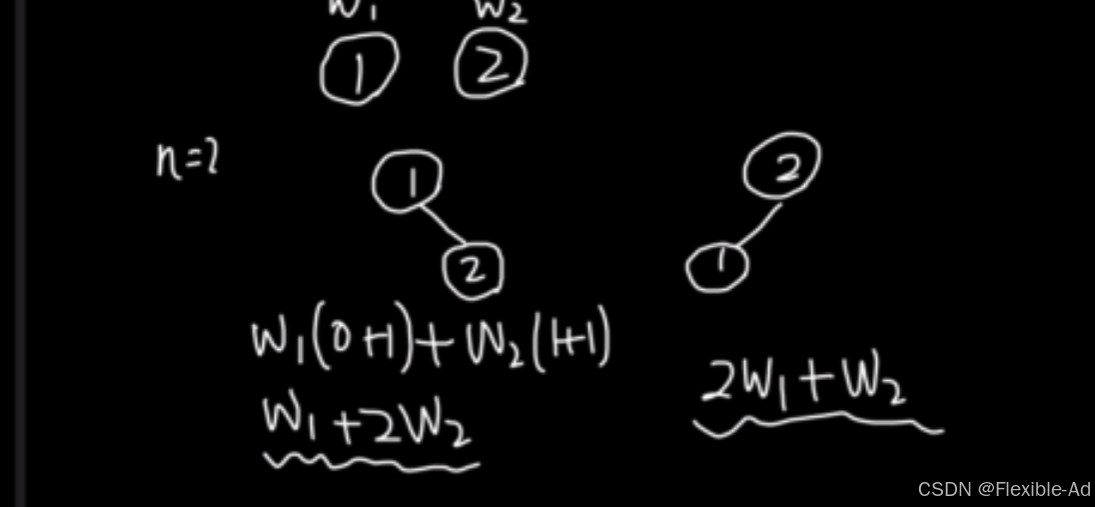
 ​​再举一个例子，以下为n=3的求解，可以发现，当n越大时我们要列举的可能性越来越多，那么，怎么样才能更快速地找到最优二叉树的排列情况呢？

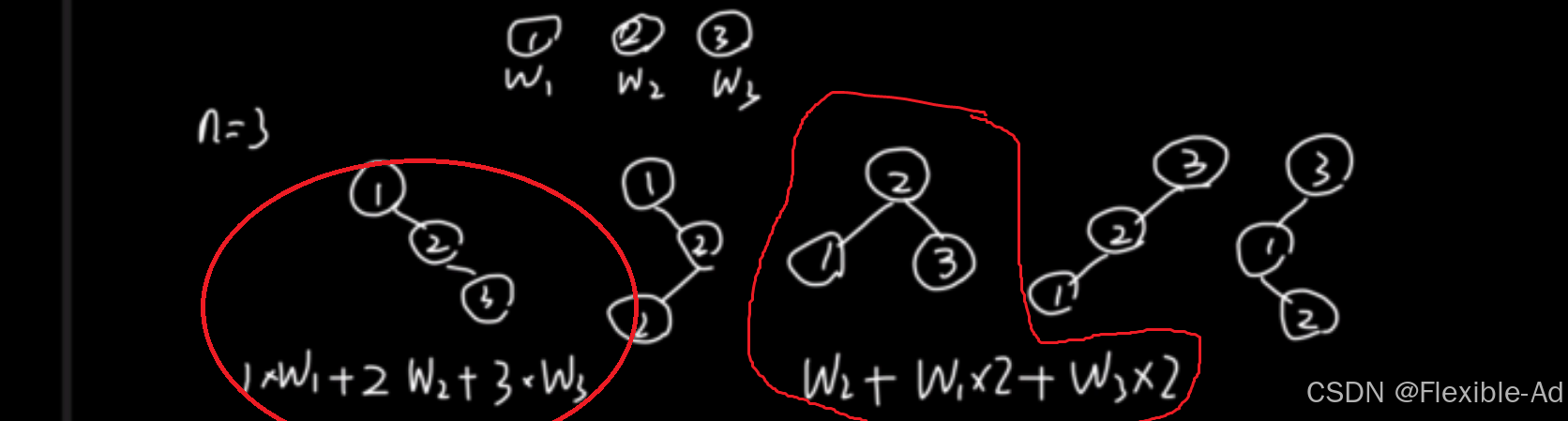
我们发现，贪心算法并不可靠，寻找不出最优情况，因而，应该采用动态规划思想

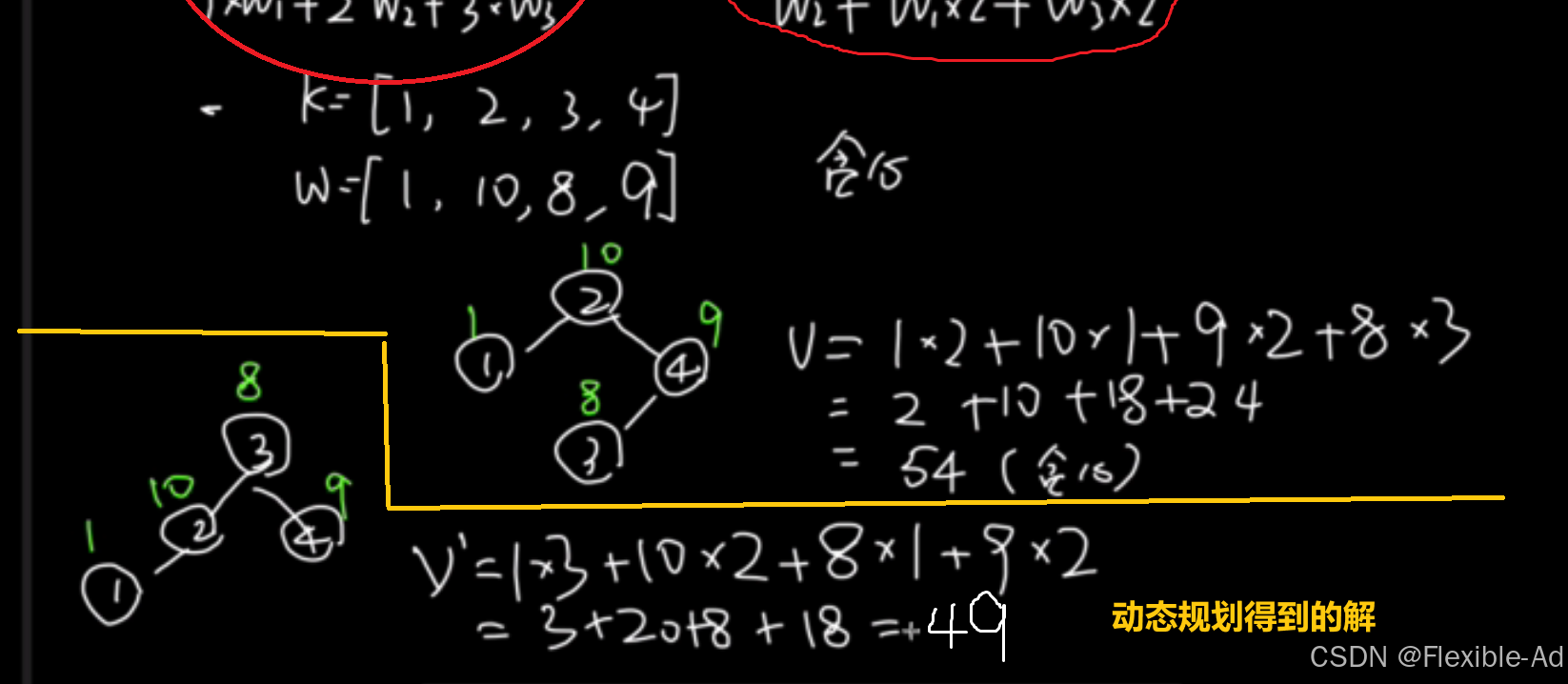
动态规划求解思路 

以下为运用动态规划思想求解的相关思路： （绿色 标记部分为我们dp【1，2】最终需要的解）

将公式总结整理，可得到：

现在来构建相关表格，i表示起始结点序号，j表示终止结点序号

由于i<j,所以i>j处都打×（在算法里就是相当于把他们都标记为0），当i=j时，最小求值就为它本身，先将以上两种情况填入表格

 我们再来填一填其他的，举个例子，求出d【1，2】的最小值，可知，当根节点为2的时候能得到最小值，在表格内记录下最小值与该最小值的根节点的位置

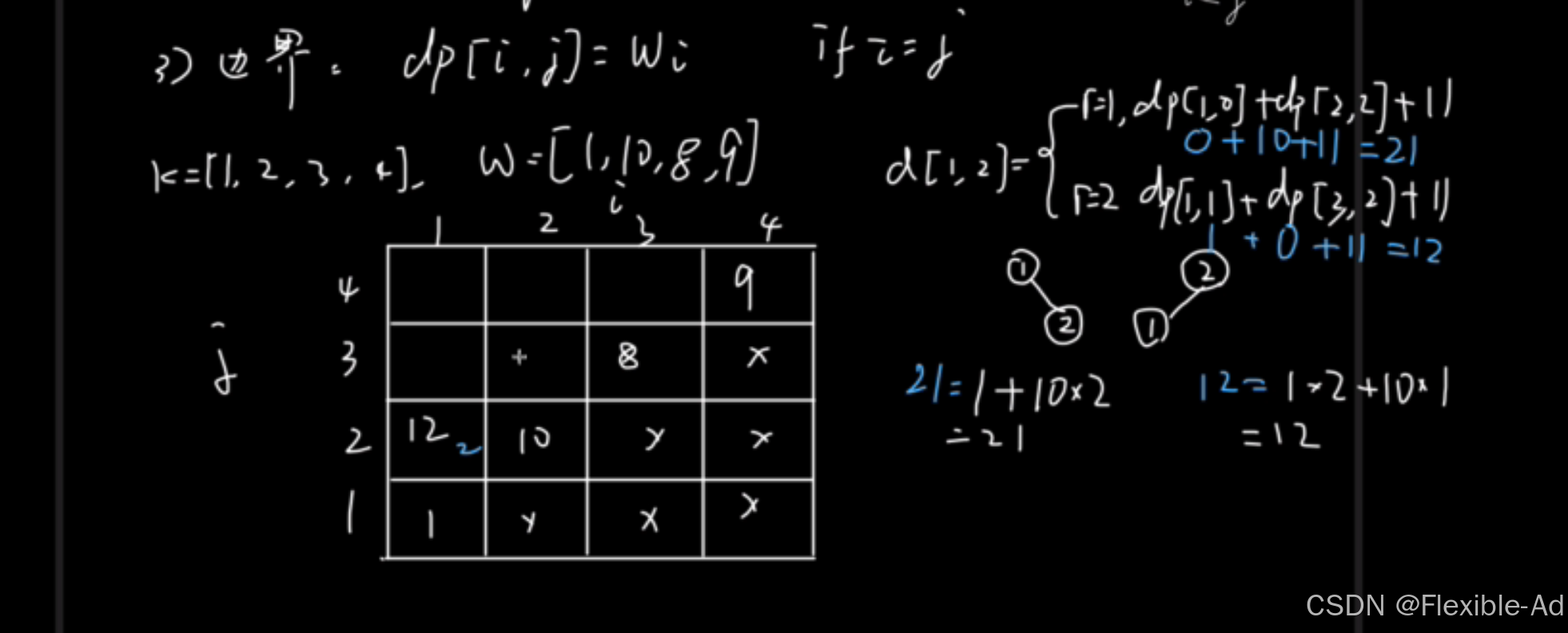
 将其他结点按照以上方法填入表格后，我们来看看最后一个结点，也就是我们要找的整棵树的排序方式，是怎么计算出来的呢

 由表格，我们画出对应的树

代码实现 

def optimal_bst(k,w):
    #创建一个二维数组,大小为n+1*n+1，最后一行一列是为了防止，当root=j时，
    # root+1形成溢出设置的
    n=len(k)
    #现将所有结点置为0
    arr=[[0]*(n+1) for i in range(n+1)]
    #当i=j时，将结点值等于权值w
    for i in range(n):
        arr[i][i]=w[i]
    for length in range(2,n+1):#树的长度2~n
        for i in range(n-length+1):#i的起始位置为0~n-length
            j=i+length-1
            #初始化为最大值，方便最小值的查找
            arr[i][j]=float('inf')
            sumw=sum(w[i:j+1])#规则是包含了i到j的总和
            #划分出了不同规模的树，从i-j
            #寻找最优的根节点,范围为第i个数到第j个数
            for root in range(i,j+1):
                sumAll=arr[i][root-1]+arr[root+1][j]+sumw
                if sumAll<arr[i][j]:
                    arr[i][j]=sumAll

    return arr[0][n-1]
ki = [1, 2, 3,4]
wi = [1,10,8,9]
result = optimal_bst(ki, wi)
print("最优二叉搜索树的最小成本:", result)

外层循环 for length in range(2, n + 1)：控制子树的长度（节点数量）。从长度为 2 开始，逐步增加到 n（即整个关键字序列构成的树），因为长度为 1 的情况已经在前面单独处理过了。

中层循环 for i in range(n - length + 1)：对于每个子树长度 length，确定子树的起始索引 i。通过 n - length + 1 可以确保在关键字序列范围内遍历所有可能的子树起始位置。例如，当 length 为 2 时，i 可以从 0 到 n - 1；当 length 为 3 时，i 可以从 0 到 n - 2，以此类推。

内层循环 for root in range(i, j + 1)：对于每个确定的子树范围（由 i 和 j 确定，其中 j = i + length - 1），尝试不同的根节点 root。这里的 root 从 i 到 j 遍历，即遍历子树范围内的每个关键字作为可能的根节点。 

b站相关视频

Ch9.8