学习日历day05 动态规划及最小编辑距离的应用（笔记）

以下动态规划介绍学习笔记来自于b站奇乐编程学院10分钟彻底搞懂“动态规划”算法，不懂的uu可以b站搜索视频观看

动态规划介绍

典型例子：

给一个数组要求找出最长递增子序列长度

我们常用暴力枚举法来实现寻找最长子序列，并总是记录下最长序列长度 

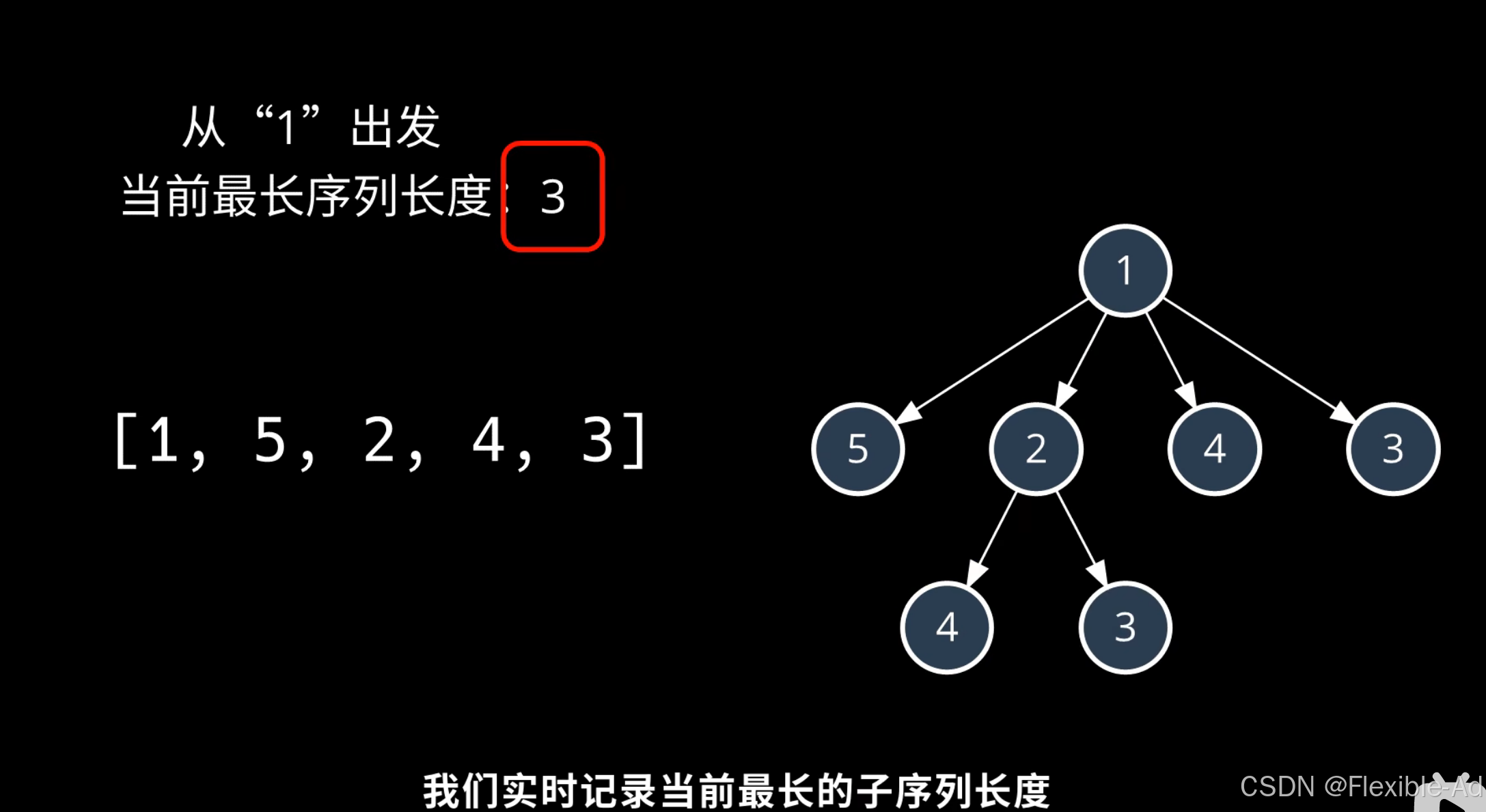
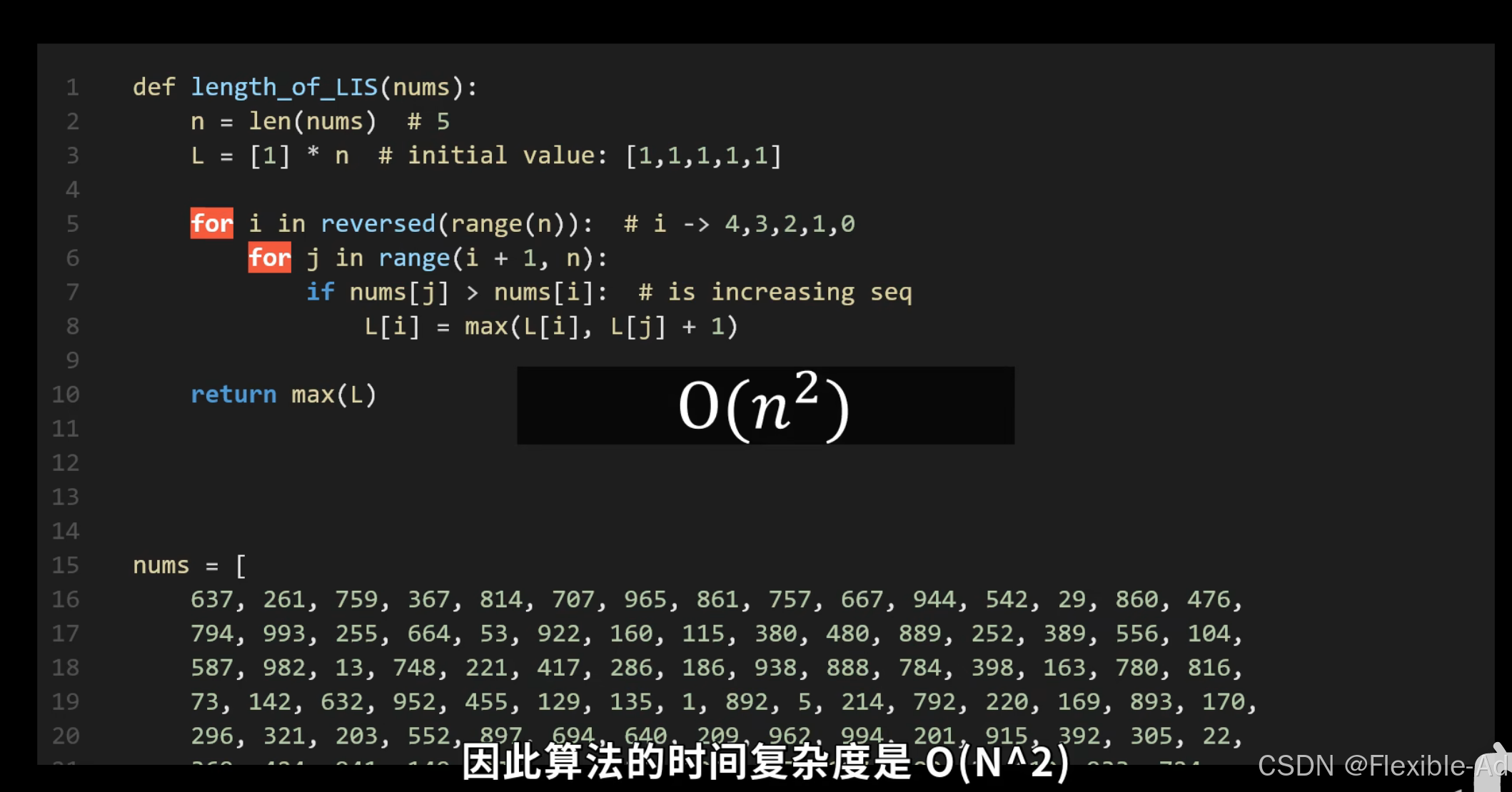
暴力枚举法算法实现：

定义一个函数L，返回值为从数组第i个元素开始的最长子序列，从第i+1个元素开始比较，如果第I+1个大于第i个元素，调用自身函数递归，运算从（i+1）到len（nums）的最长子序列，再往后＋1得到目前这个序列的总长度。

用max-len记录最长长度，在遍历所有的j后记录下最长的子序列长度，再返回max-len

再定义另一个函数，寻找从不同数组元素索引开始找到的最长子序列长度，返回最长子序列长度 

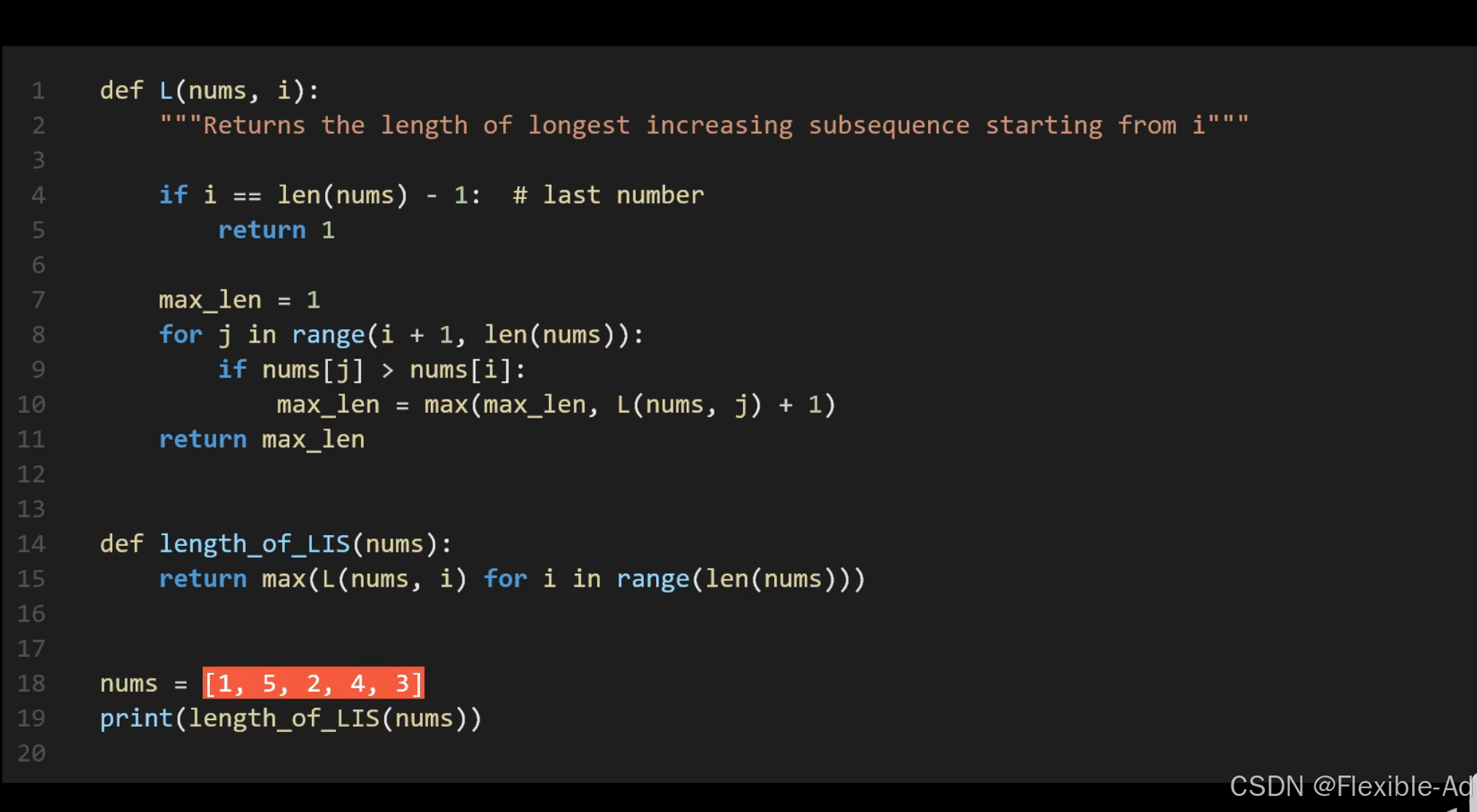
暴力枚举法缺点：

时间复杂度为O（n*2^n）时间复杂度太高运算速率慢

解决方法：创建一个空间，将相同的运算保存下来，之后再遇到直接取数字而不用再次运算

动态规划就是避免重复运算加快整个运算过程，用“空间”换“时间”

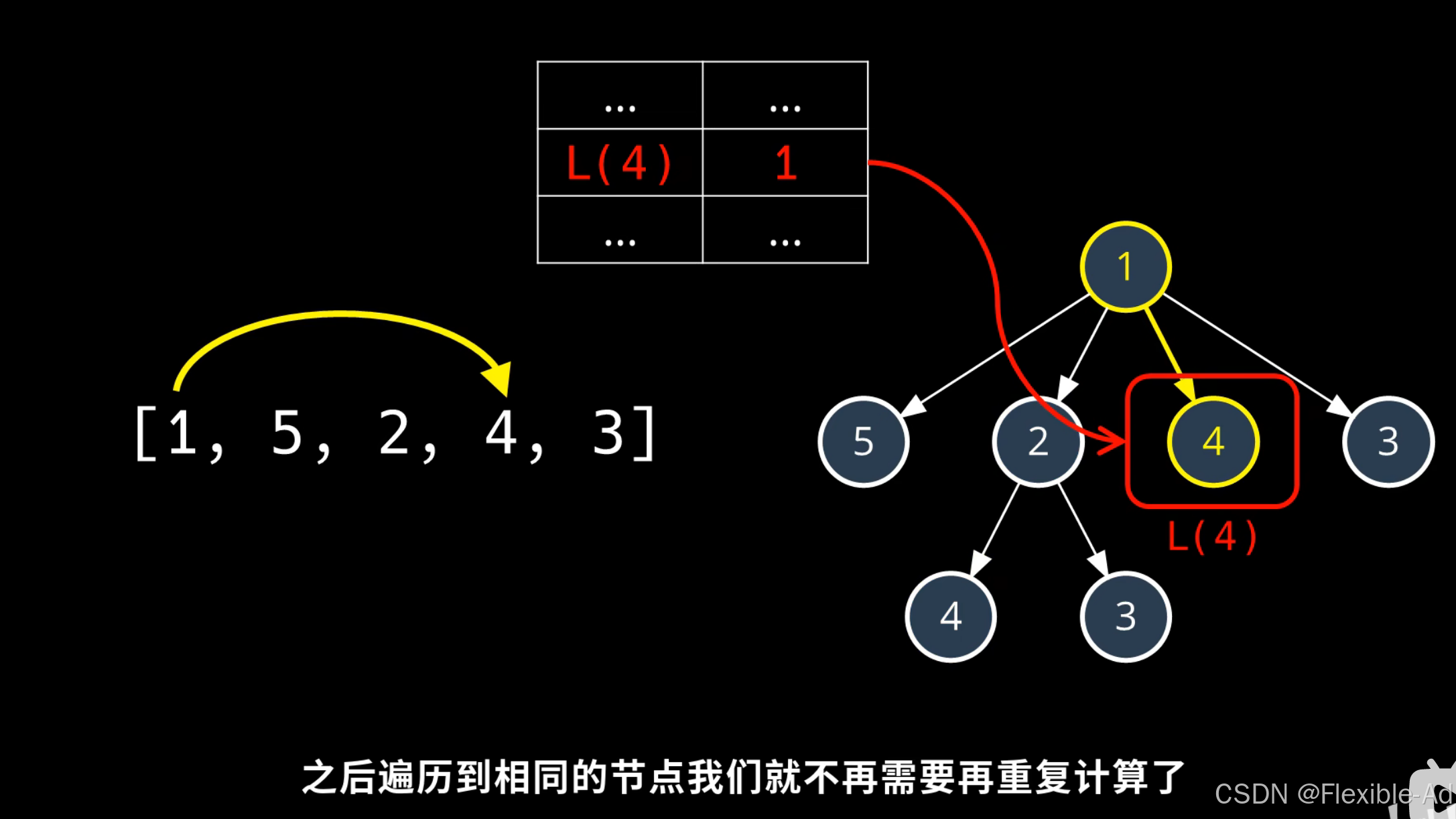
运用字典保存运算结果 

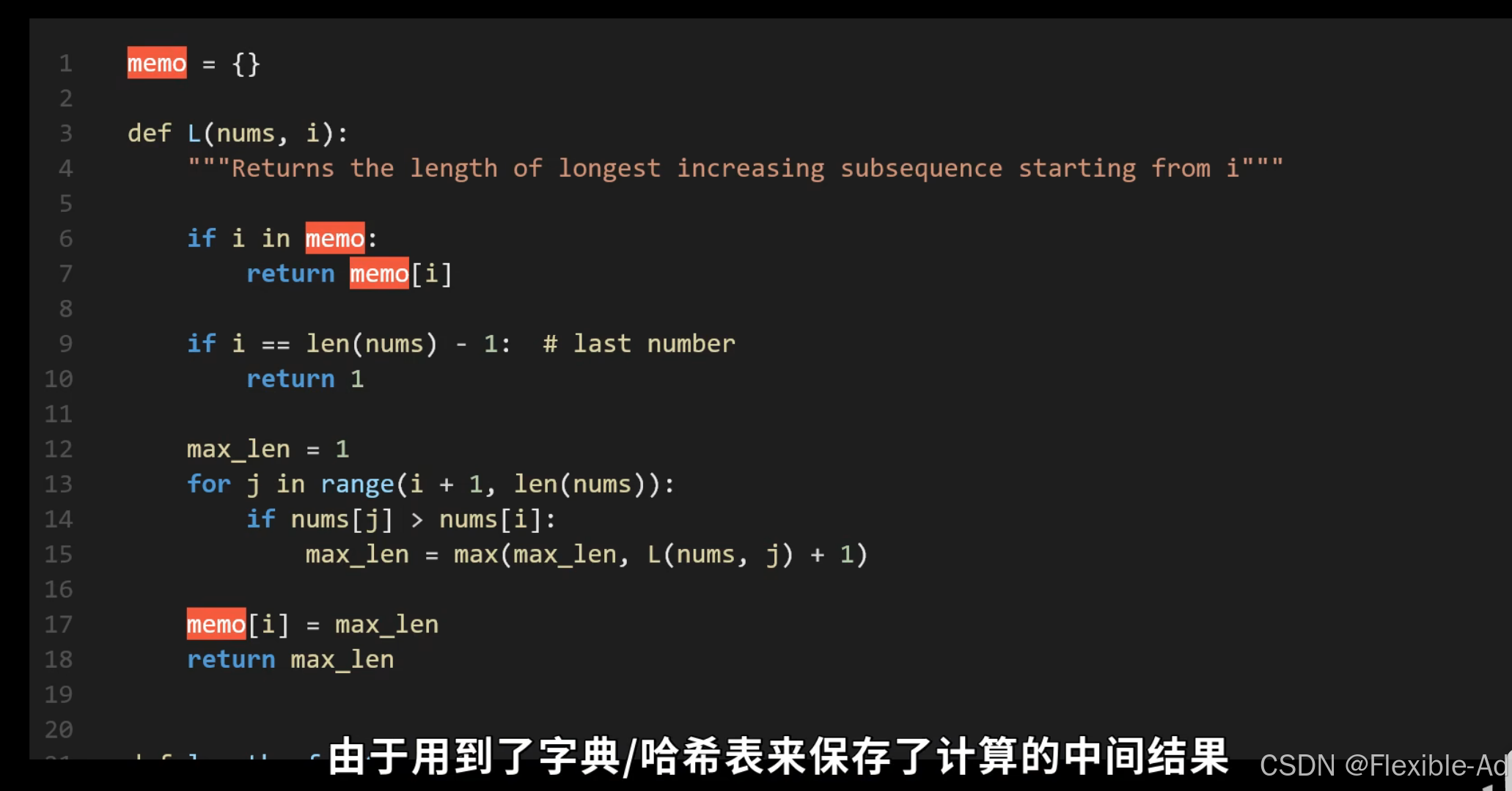
非递归实现动态规划 

算法实现

外层循环：从下往上遍历，对应上图从L（4）往L（0）遍历运算

内层循环：L[i]表示将L（3）、L（4）中的最长子序列长度存下，其中max(…)中相等价于取{}中的max值 

 

最小编辑距离的应用

以下最小编辑距离的应用笔记整理自b站 邋遢大哥233[轻松掌握动态规划]6.编辑距离 视频，不懂的uu可以b站搜索视频观看

实践例子：字符串最短编辑距离

问题引入：

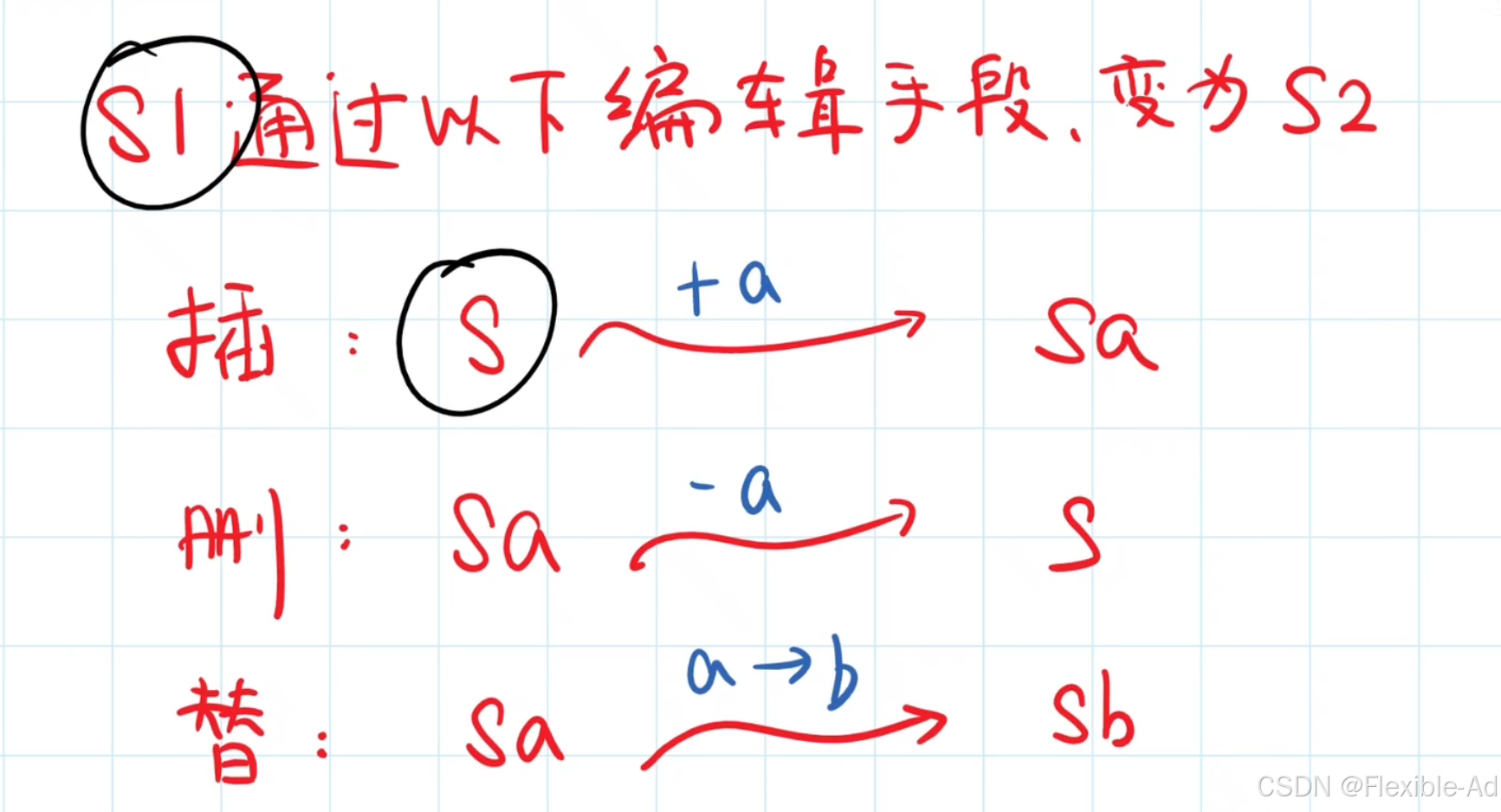
具体例子：sun转化为satur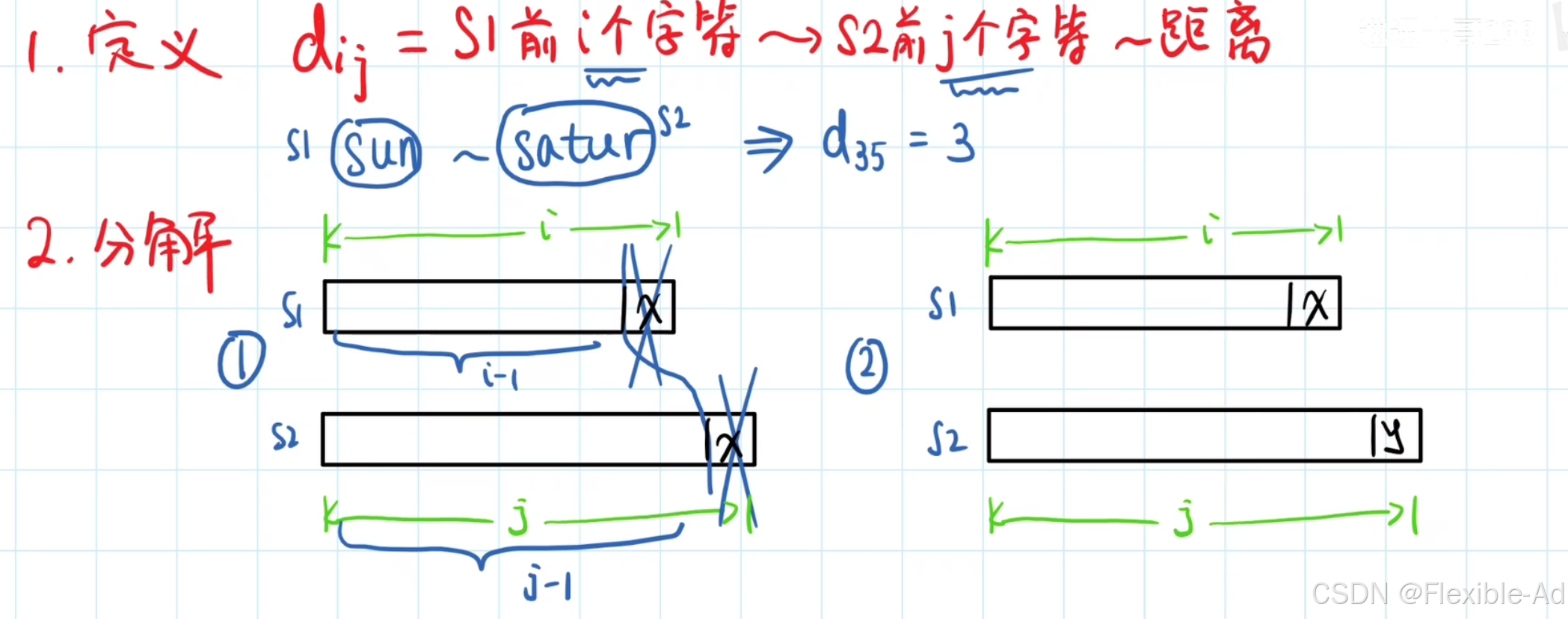 

若最后两个字符相等，那么会步长不用加1，为以上情况1

相等操作：if( s1[i-1]==s2[j-1]) D[i][j]=D[i-1][j-1]

if分支使用 i-1 和 j-1 而不是直接使用 i 和 j 是因为在此处比较的是字符串内的元素，D列表内0不代表任意元素，而字符串0索引有对应代表的元素，需要减一

如果最后两个字符不相等，那么最后一步在s1的基础上做替换，删除或者添加，取哪个操作取决于以下三个操作后哪个D[i][j]最小

以下三个操作完成后取min（）

替换操作（s1最后一个字符替换为s2最后一个字符）：D[i][j]=D[i-1][j-1]+1（此时比较s1的i-1个元素于s2的j-1个元素是否相同，+1为做替换操作，步数加1）

插入操作（s1插入新字符为s2最后一个字符）：D[i][j]=D[i][j-1]+1（此时比较s1的i个元素于s2的j-1个元素是否相同，+1为做插入操作，步数加1）

删除操作（s1删除最后一个字符）：D[i][j]=D[i-1][j]+1（此时比较s1的i-1个元素于s2的j个元素是否相同，+1为做删除操作，步数加1）

注意：这里D[0][0]表示空字符

 

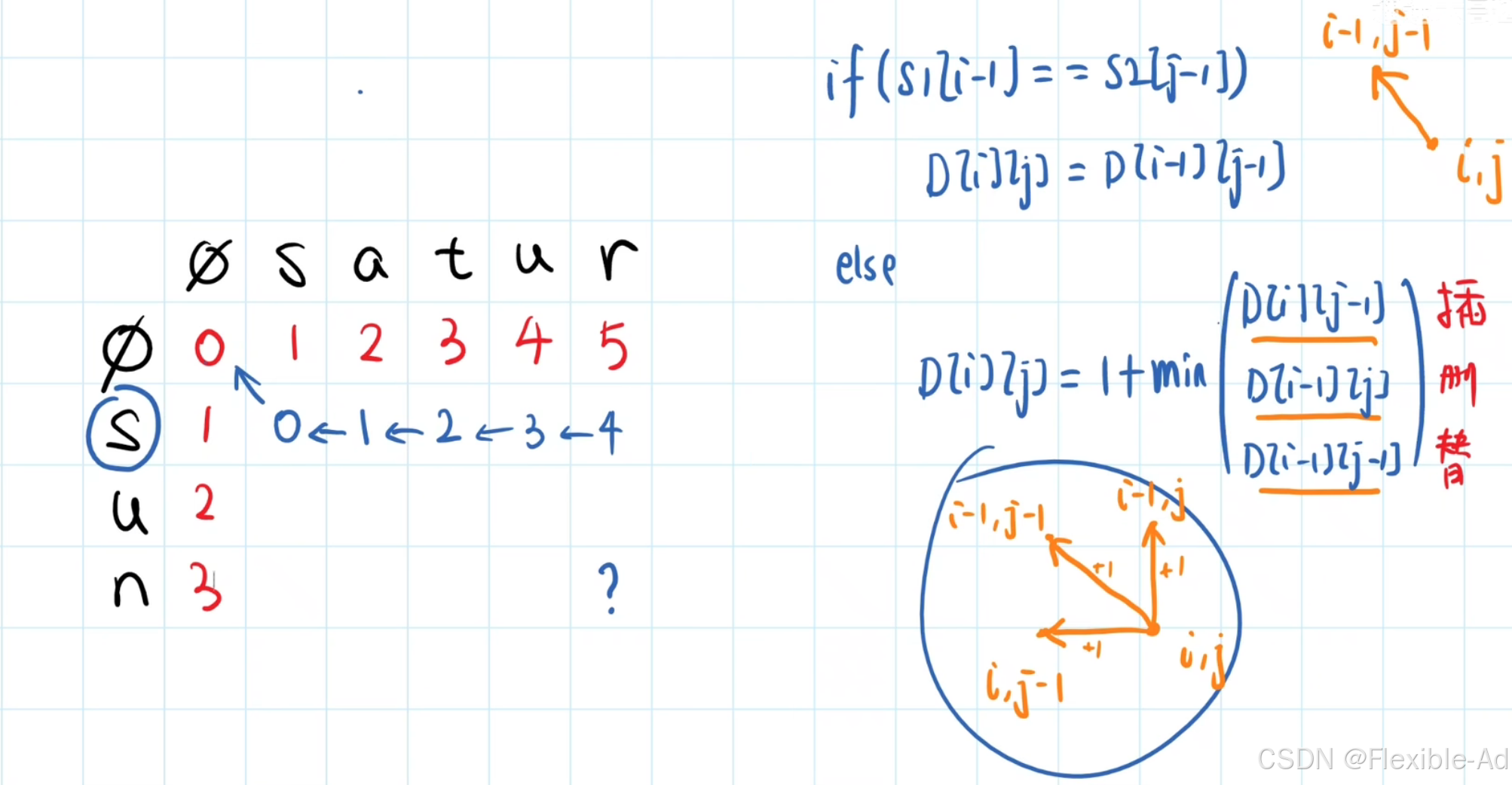
 ？为待求解数字，表格纵向为i轴，横向为j轴，D[1][5]表示将s转换为satur需要几步操作？

 D[i]和D[j]一样，直接取左上角数字，D[i]和D[j]不一样，取三个方向上的最小值再加1

代码实现

# 求最小编辑距离
def minDistance(string1,string2):
    len1 = len(string1)
    len2 = len(string2)
    if len1 == 0:
        return len2
    if len2 == 0:
        return len1
    #创建二位列表，把元素初始化为0，大小为（len1+1）*（len2+1）
    step = [[0]*(len2+1)for i in range(len1+1)]
    # 设置第二个字符串为空串时的编辑距离
    for i in range(1,len1+1):
        # ********** Begin ********** #    
        step[i][0]=i# 将string1转换为空串需要i次删除
        # ********** End ********** #
    # 设置第一个字符串为空串时的编辑距离
    for j in range(1,len2+1):
        # ********** Begin ********** #    
        step[0][j]=j# 将空串转换为string2需要j次插入
        # ********** End ********** #
    # 设置两个字符串都非空时的编辑距离
    for i in range(1,len1+1):
        for j in range(1,len2+1):
            # ********** Begin ********** # 
            # 如果最后一个字符相同，则不需要额外的操作   
            if string1[i-1]==string2[j-1]:
                step[i][j]=step[i-1][j-1]
            else:
             # 否则取插入、删除、替换三种操作中的最小值加一
                step[i][j]=min(step[i-1][j],step[i][j-1],step[i-1][j-1])+1
            
            # ********** End ********** #
    return step[len1][len2]