学习日历day07 动态规划-矩阵连乘问题（笔记）

以下为观看b站up四七777777的动态规划 矩阵连乘问题视频后做的相关笔记，有不懂的uu可以上b站观看相关视频

为什么要探讨矩阵连乘次序问题：

矩阵不同次序的相称会发生不同的乘法运算量，为了使乘法运算量最小，我们需要探讨矩阵相乘的次序。

比如：(A1A2)A3次数为10*100*5（a1a2的乘法次数）+10*5*50（a1a2相乘得到的新矩阵与a3的乘法次数）=7500

A1（A2A3）次数为100*5*50（a2a3的乘法次数）+10*100*50（a2a3相乘得到的新矩阵与a1的乘法次数）=75000

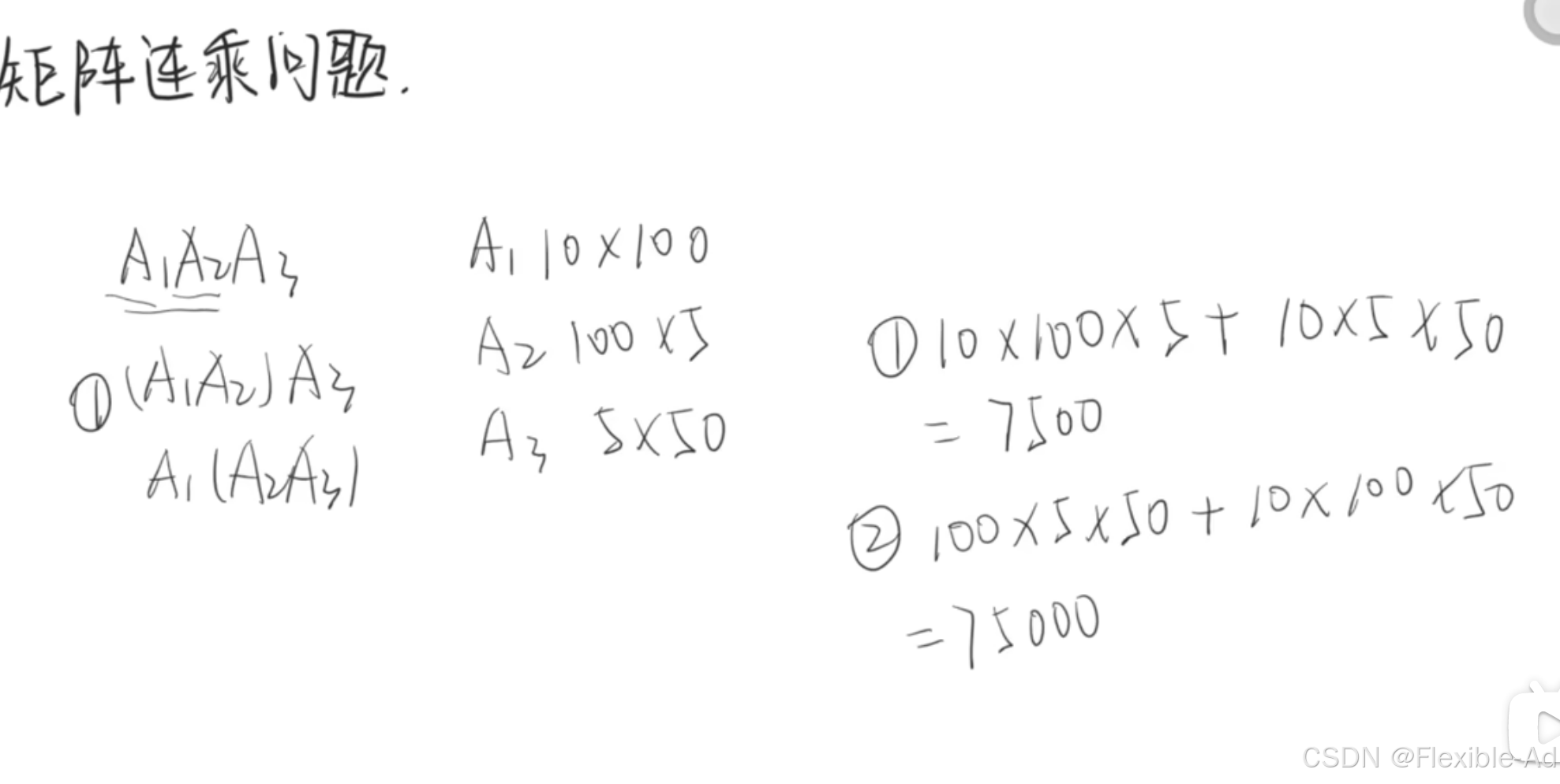
矩阵连乘用到的动态规划思想：

动态规划的思想是将大问题拆解为小问题，大问题依赖于小问题中的数据来源。通过寻找小问题中最优解来解决大问题中最优解问题，且每次将小问题的最优解记录，方便快速的查找

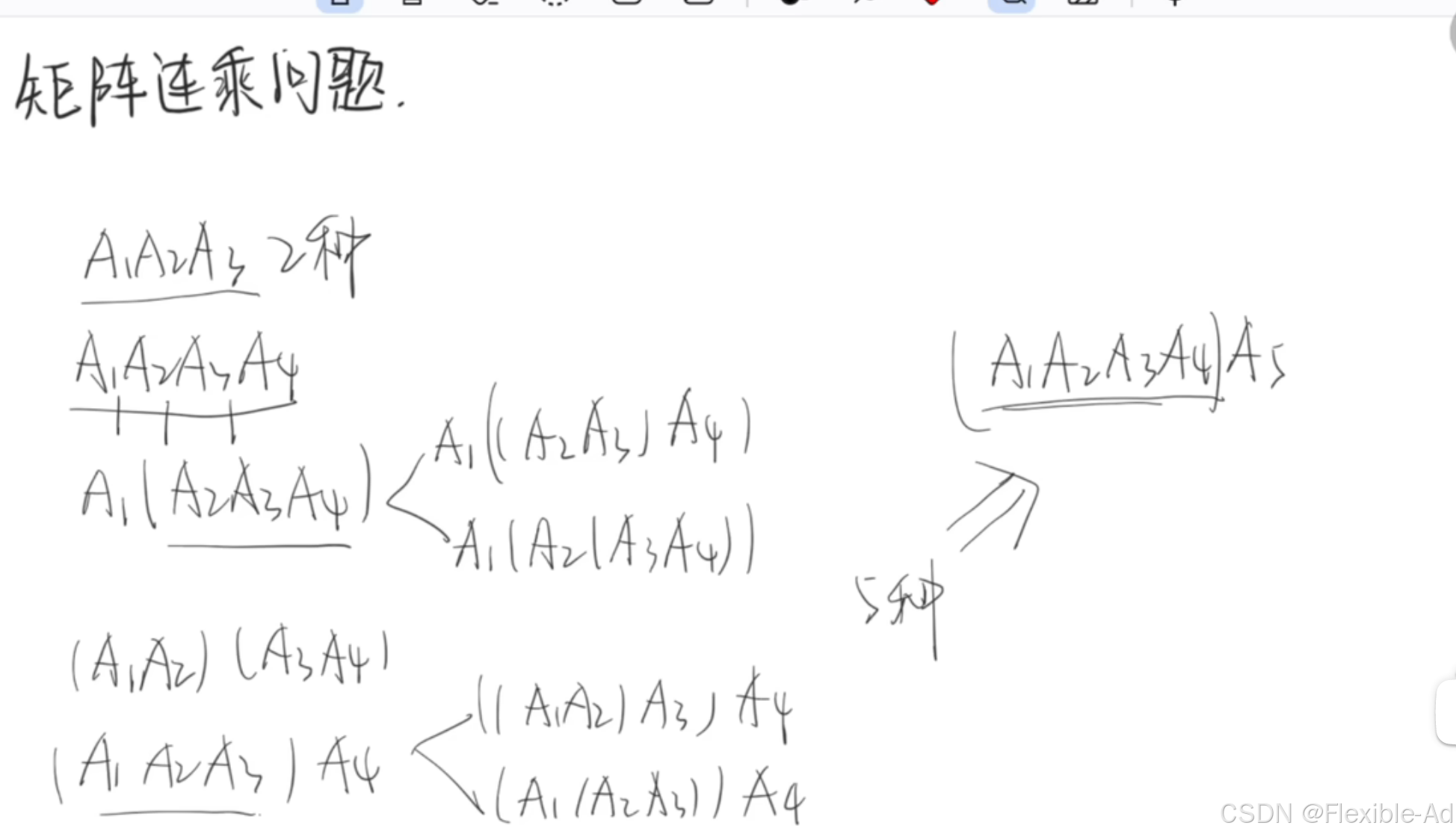
由上可知，有3个矩阵时有两种组合，我们可以先求出这两种组合里的最小值，记录。那么有四个矩阵时可以将矩阵分为1+3，2+2的组合。由下图可知，当矩阵为1+3组合时候，3有两种组合方法，由于上面子问题已经解决3的组合方案中哪个更小的问题，我们可以直接选取出来最优解。

m[i][j]代表从Ai矩阵连乘到Aj矩阵的最小乘法次数 

我们说将矩阵分成不同的组合在进行比较，此时可以引入一个k，k代表分割点，将一个矩阵分成两个不同的组合m[i][k]和m[k+1][j]。k分割点的位置在i<=k<j范围内的任意一个数。

分成两个不同的矩阵组后，只需要分别找到这两个矩阵组里面的最优解，便可以得到当k等于某个数时，该矩阵组的最优解。由于k有多个，需要将不同取值的k得到的所有最优解进行比较，才能得到该矩阵最终的最优解。

比如：(A1A2)A3的k为2，将矩阵分成了1-2与3的两个矩阵组，需要求1-2的最优解与3的最优解，再将其相加且加上(A1A2)与A3的相乘次数。

A1（A2A3）的k为1，将矩阵分成了1与2-3的两个矩阵组，需要求1的最优解与2-3的最优解，再将其相加且加上A1与（A2A3）的相乘次数。

比较上述两种不同解哪种次数最少，将最少的次数7500作为m[1][3]的值

简化运算

最终我们在求(A1A2)与A3的相乘次数的时候，根据矩阵乘法次数规律，不难发现需要用到a1的行乘ak（也就是a2）的列乘a3的列，即公式为PiQkQj（P为行，Q为列），那么此时需要引入一个二维数组来存储行列的值吗？no！我们可以将二维数组简化为一维数组Q[]。因为Pi等于Qi-1。（因为矩阵是连乘的，前一个矩阵的列等于后一矩阵的行）。当矩阵数目为n时，Q[]只需要存储n+1个数。

 具体例子

根据给的矩阵定义q

m[i][j]当i=j时等于0，因为只有一个数，也就是自己，做不了乘法，为0，对角线填0

下三角i>j为0，矩阵乘法有顺序，不可逆

i>j,m[i][j]含义如图中红字

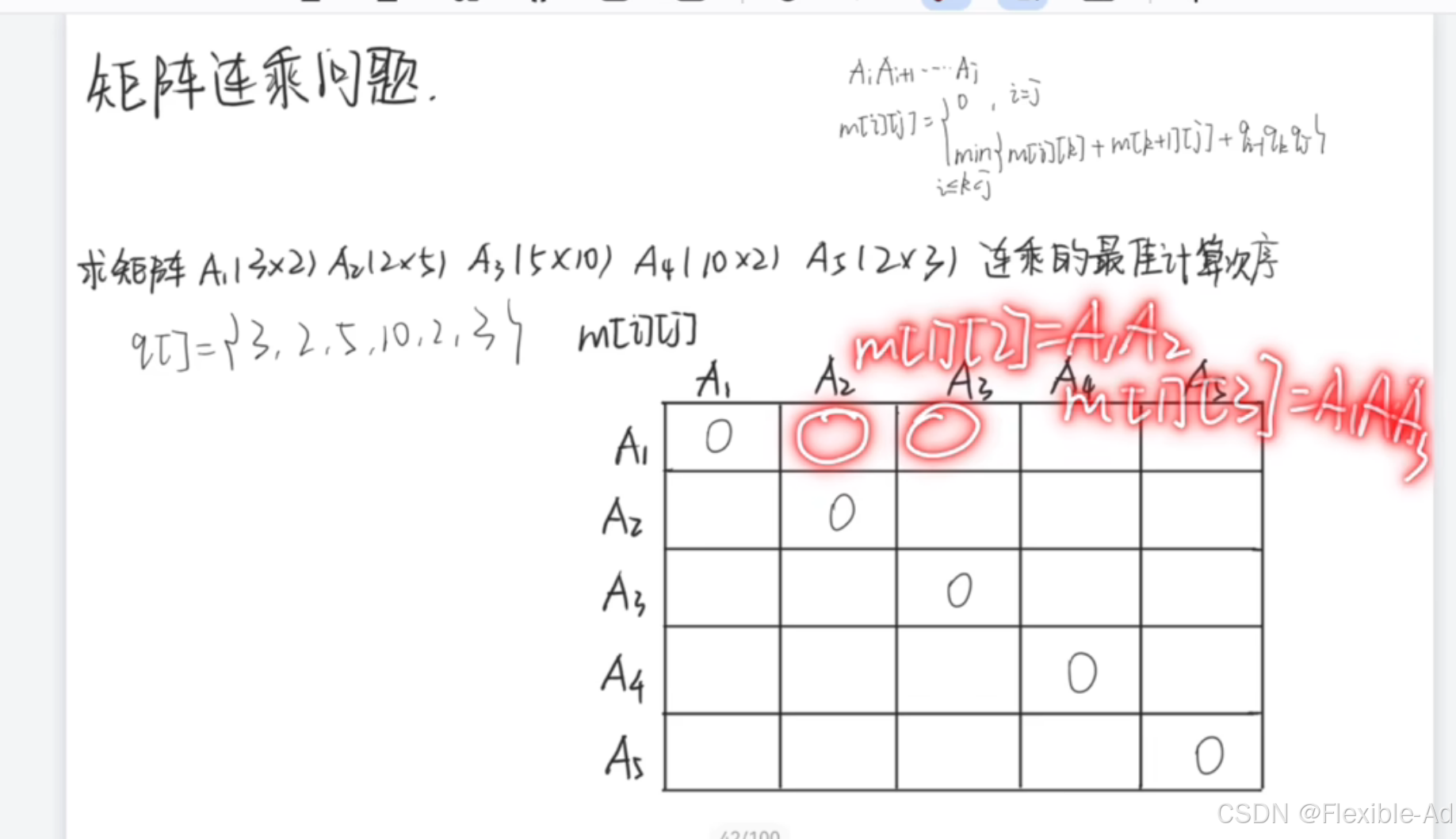
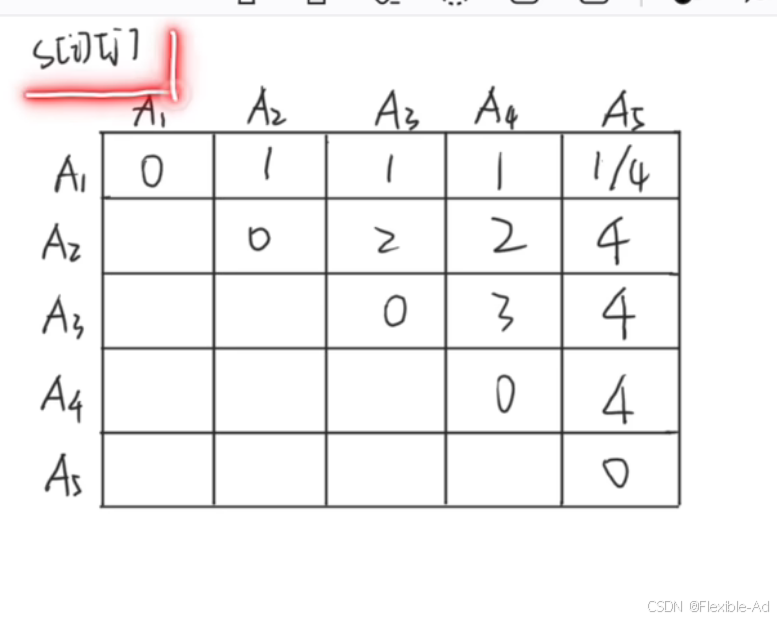
 得到数m[1][2]过程

 得到数m[1][3]过程 

记录下断点k的位置，方便后续括号打印操作，即这个效果

“最佳括号化方案:((A1(A2A3))((A4A5)A6)) ”

代码实现 

def matrix_chain_order(p):
    #矩阵的数目
    n=len(p)-1
    #初始化记录最小值的矩阵m与分割点矩阵s
    m=[[0]*n for i in range(n)]
    s=[[0]*n for i in range(n)]#矩阵为n*n
    #先将链长度小的m[i][j]最小值填充，因为后面计算链长度大的m[i][j]需要用到链长度小的m[i][j]的值
    #为1不用计算，因为乘法次数为0
    for l in range(2,n+1):
        #求出该链长下所有可能组合
        #表示i可能的所有取值
        for i in range(n-l+1):
            #对应i取值下j的取值
            j=i+l-1
            #给m[i][j]赋一个最大值
            m[i][j]=float('inf')
            #探索不同断点k下m[i][j]可以拥有的最小值
            for k in range(i,j):
                #计算该断点下m[i][j]的值
                q=m[i][k]+m[k+1][j]+p[i]*p[k+1]*p[j+1]
                if q<m[i][j]:
                    #更新最小值
                    m[i][j]=q
                    #更新断点位置
                    s[i][j]=k
    #返回记录最小值的矩阵m，以及断点矩阵s
    return m,s

#根据记录的断点将最佳括号方案进行打印
def print_optimal(s,i,j):
    if i==j:
        print(f"A{i+1}",end="")
    else:
        print("(",end="")
        #递归调用，根据最佳断点的记录将矩阵链切割为两段
        print_optimal(s,i,s[i][j])
        print_optimal(s,s[i][j]+1,j)
        print(")",end="")

#A1: 30x35
#A2: 35x15
#A3: 15x5
#A4: 5x10
#A5: 10x20
#A6: 20x25
p = [30, 35, 15, 5, 10, 20, 25]  # 矩阵维度列表
m, s = matrix_chain_order(p)

print("最优解的成本矩阵:")
for row in m:
    print(row)

print("\n最佳括号化方案:")
print_optimal(s, 0, len(p) - 2)

为方便理解def matrix_chain_order(p):中的三重循环代码，举出一些具体例子：

A1: 30x35
A2: 35x15
A3: 15x5
A4: 5x10
对应的维度列表 p 为 [30, 35, 15, 5, 10]。

初始化
首先，我们初始化矩阵 m 和 s，其中 m 用于存储最小乘法次数，s 用于存储最佳的分割点。

n = len(p) - 1  # 矩阵的数量
m = [[0] * n for _ in range(n)]
s = [[0] * n for _ in range(n)]

对于这个例子，n 为 4，所以 m 和 s 都是 4x4 的矩阵，初始值为 0。

外层循环
外层循环变量 l 表示当前考虑的矩阵链的长度，从 2 开始（因为单个矩阵的乘法成本为 0），一直到 n。

for l in range(2, n + 1):

对于这个例子，l 将依次取值 2, 3, 4。

内层循环
内层循环变量 i 表示当前子问题的起始矩阵索引，j 表示结束索引。

for i in range(n - l + 1):
    j = i + l - 1
    m[i][j] = float('inf')

对于 l = 2：i 可以取 0, 1, 2     j 分别为 1, 2, 3

对于 l = 3：i 可以取 0, 1         j 分别为 2, 3
对于 l = 4：i 只能取 0              j 为 3
每次进入内层循环时，我们将 m[i][j] 初始化为无穷大，表示还没有找到有效的解。

尝试所有可能的分割点
对于每一个 i 和 j，我们尝试所有可能的分割点 k，计算从 i 到 k 和从 k+1 到 j 的乘法次数加上这两部分相乘的次数。

for k in range(i, j):
    q = m[i][k] + m[k + 1][j] + p[i] * p[k + 1] * p[j + 1]
    if q < m[i][j]:
        m[i][j] = q
        s[i][j] = k  # 记录断点

具体示例
假设 l = 2，i = 0，j = 1，即考虑矩阵 A1 和 A2 的乘法。

m[0][1] 初始为无穷大。
尝试分割点 k = 0：
q = m[0][0] + m[1][1] + p[0] * p[1] * p[2]
m[0][0] 和 m[1][1] 都为 0，因为单个矩阵的乘法成本为 0。
q = 0 + 0 + 30 * 35 * 15 = 15750
因为 q < m[0][1]，所以更新 m[0][1] = 15750，s[0][1] = 0。
接下来，继续处理其他 i 和 j 的组合，直到所有可能的链长都处理完毕。

最终结果
经过所有迭代后，m 和 s 矩阵将包含所有子问题的最优解。最终的 m[0][3] 将是计算所有矩阵乘法的最小乘法次数，s 矩阵将记录最佳的分割点，用于构造最优的括号化方案。