先序、中序、后序、层序遍历（递归与非递归）代码实现

欢迎批评指正

思路总结：

不管是递归还是非递归，树的结构都是有根节点，左子节点，右子节点构成，注意：这里的左子节点，右子节点在下一次循环也可以作为根节点。我们可以用以下递归/循环的思路，以前序遍历为例，我们可以将思路简化，每次只实现当前节点的打印，用递归或循环，将整棵树按照根节点，左子节点，右子节点访问顺序打印出来。

创建一颗二叉树

typedef char Elemtype;
typedef struct node {
    Elemtype data;//存储结点的内容
    struct node* lchild;//左子节点地址
    struct node* rchild;//右子节点地址
}BTSNode;

先序遍历

先序遍历指的是访问树结点的顺序为：根节点，左子节点，右子节点

先序遍历递归版

void PreOrder(BTSNode* b) {
    if (b != NULL) {
        printf("%c", b->data);
        PreOrder(b->lchild);
        PreOrder(b->rchild);
    }
}

 思路：每次先访问根节点并打印，再向下访问左子节点调用本函数，接着递归调用右子节点。不管是左子节点还是右子节点，再次调用函数它就成为根节点，就会被打印，但是总体打印顺序有先后，顺序为根->左子->右子。

先序遍历非递归版（创建栈）

void PreOrder1(BTSNode*b){
    //创建一个栈
    BTSNode* St[100];
    BTSNode* p;
    int top = -1;
    if (b != NULL) {
        top++;
        St[top] = b;
        while (top > -1) {
            p = St[top];
            top--;
            printf("%c", p->data);
            if (p->rchild != NULL) {
                top++;
                St[top] = p->rchild;
            }
            if (p->lchild != NULL) {
                top++;
                St[top] = p->lchild;
            }
 
        }
    }
}

思路：为了实现递归的效果，可以运用循环和栈，栈可以记录节点。 创建一个栈，首先将根节点放入，每次循环开始，弹出栈顶元素并记录为p，且每次打印栈顶元素，根据栈先进后出的特性，可以先放入p的右子节点，再放入p的左子节点。下次循环必定弹出左子节点作为根节点p，如此循环下去就可以实现效果。

中序遍历

中序遍历指的是访问树结点的顺序为：左子节点，根节点，右子节点

中序遍历递归版

void InOrder(BTSNode* b) {
    if (b != NULL) {
        InOrder(b->lchild);
        printf("%c", b->data);
        InOrder(b->rchild);
    }
}

思路：先访问左子树再打印自己。通俗来说就是看看有没有左子节点，再打印自己。就实现了一种左子节点，根节点，右子节点的打印效果。

中序遍历非递归版

void InOrder1(BTSNode* b) {
    BTSNode* St[100];
    BTSNode* p;
    int top = -1;
    if (b != NULL) {
        p = b;
        while (top > -1 || p != NULL) {
            //将任意根节点左孩子都入栈，根节点自己为null，不入栈
            while (p != NULL) {
                top++;
                St[top] = p;
                p = p->lchild;
            }
            //弹出一个孩子并打印，并查询是否有右孩子
            if (top > -1) {
                p = St[top];
                top--;
                printf("%c", p->data);
                p->rchild;//右孩子为null没关系，不会有查询左孩子的操作，会进入弹栈操作
            }
        }
    } 
}

思路：创建一个栈，将根节点的左孩子都优先入栈，弹栈打印操作相当于完成了左孩子（根节点：有右孩子可以作为根节点）的打印，再访问该节点的右孩子。

后序遍历

后序遍历是指首先访问左子树，然后访问右子树，最后访问根节点。

后序遍历递归版

void PostOrder(BTSNode* b) {
	if (b != NULL) {
		PostOrder(b->lchild);
		PostOrder(b->rchild);
		printf("%c", b->data);
	}
}

后序遍历非递归版

后序遍历非递归版为最难的一种，以下由逻辑思路与图解将代码实现部分详细说明

整体逻辑思路

代码实现

// 后序遍历非递归函数
void postOrderTraversal(BTSNode* root) {
    if (root == NULL) {
        return;
    }

    BTSNode* stack[100];  // 定义一个栈来存储节点指针，这里假设栈大小为100，可根据实际情况调整
    int top = -1;
    BTSNode* lastchild = NULL;  // 用于记录上一个访问过的节点

    while (root != NULL || top != -1) {
        // 先将左子树节点全部入栈
        while (root != NULL) {
            stack[++top] = root;
            root = root->lchild;
        }

    
        bool flag = true;
        while (flag && top > -1) {
            root = stack[top];
            // 如果右子树为空或者右子树已经访问过，就访问该节点
            if (root->rchild == NULL || root->rchild == lastchild) {
                printf("%c ", root->data);
                lastchild = root;
                top--;
                
            }
            else {
                // 否则先处理右子树
                root = root->rchild;
                flag = false;
            }
        }
        
    }
    printf("\n");
}

lastchild原理图解

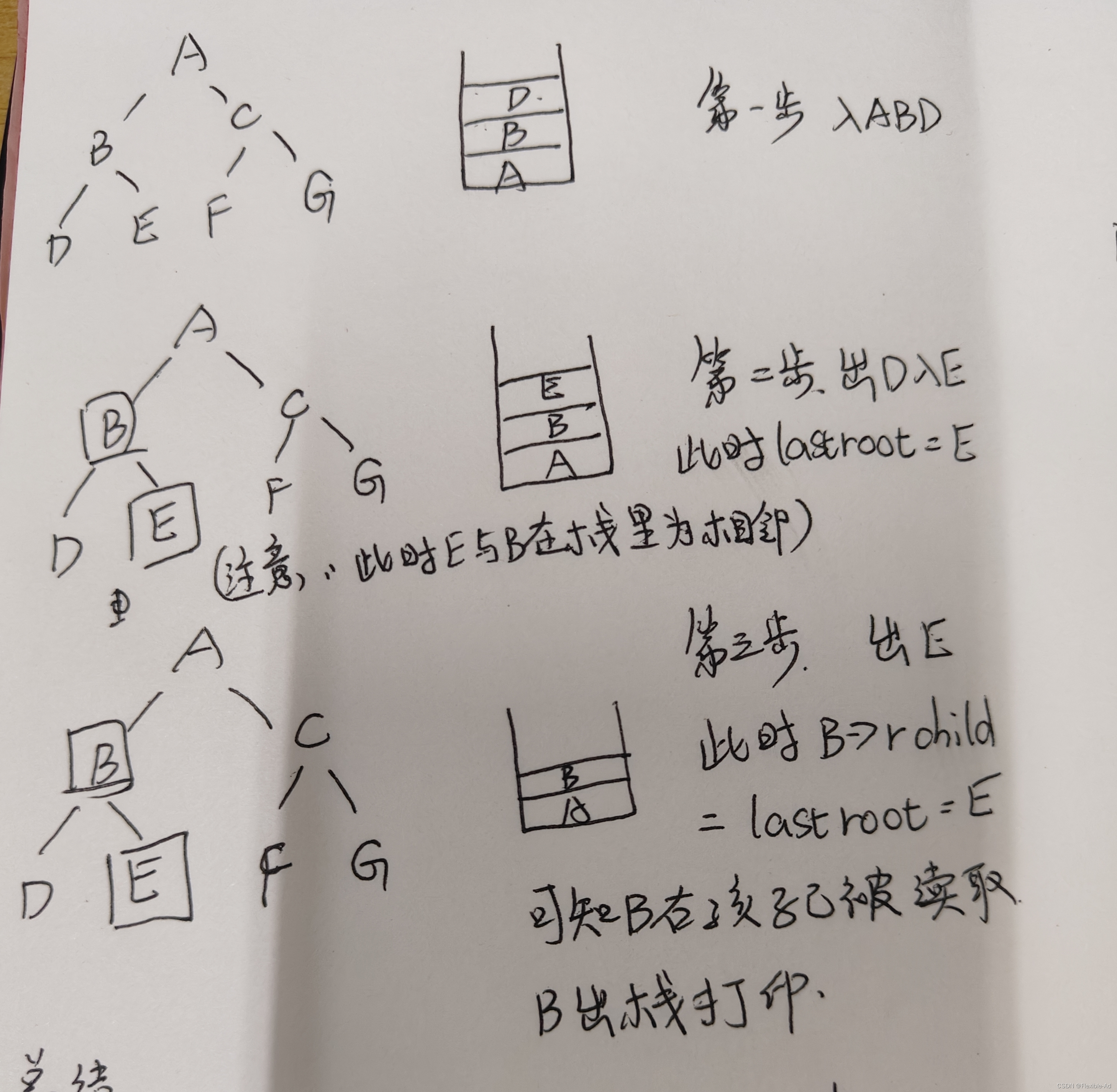
总结：形成一种根、左、右入栈的规律；且右在左出来之后再入栈，由于每次都会记录下出栈元素，当右孩子与根相邻时，lastroot起到记录是否被访问过的作用

层序遍历

层序遍历遍历顺序为自顶向下，自左向右，一层一层遍历。

根据遍历顺序，我们可以使用队列，队列的特点是先进先出，根节点先入队列，再出队列的第一个结点，判断该结点是否有左子节点或右子节点，有入队列

//层序遍历
void Travlevel(BTSNode* b) {
    BTSNode* Qu[Maxsize];//创建一个队列
    BTSNode* p;
    int front =0, rear = 0;//创建两个索引，一个指向队列头，一个指向队列尾
    if (b != NULL) {
        Qu[front] = b;
        rear++;
    }
    while (rear != front) {//相等的话表明此时队列为空
        p = Qu[front];
        front=(front + 1)%Maxsize;
        printf("%c", p->data);
        if (p->lchild != NULL) {
            Qu[rear] = p->lchild;
            rear = (rear + 1) % Maxsize;
        }
        if (p->rchild != NULL) {
            Qu[rear] = p->rchild;
            rear = (rear + 1) % Maxsize;
        }
    }
}