算法：94.实现中序遍历（3种方法：递归、迭代、Morris）Python & Java

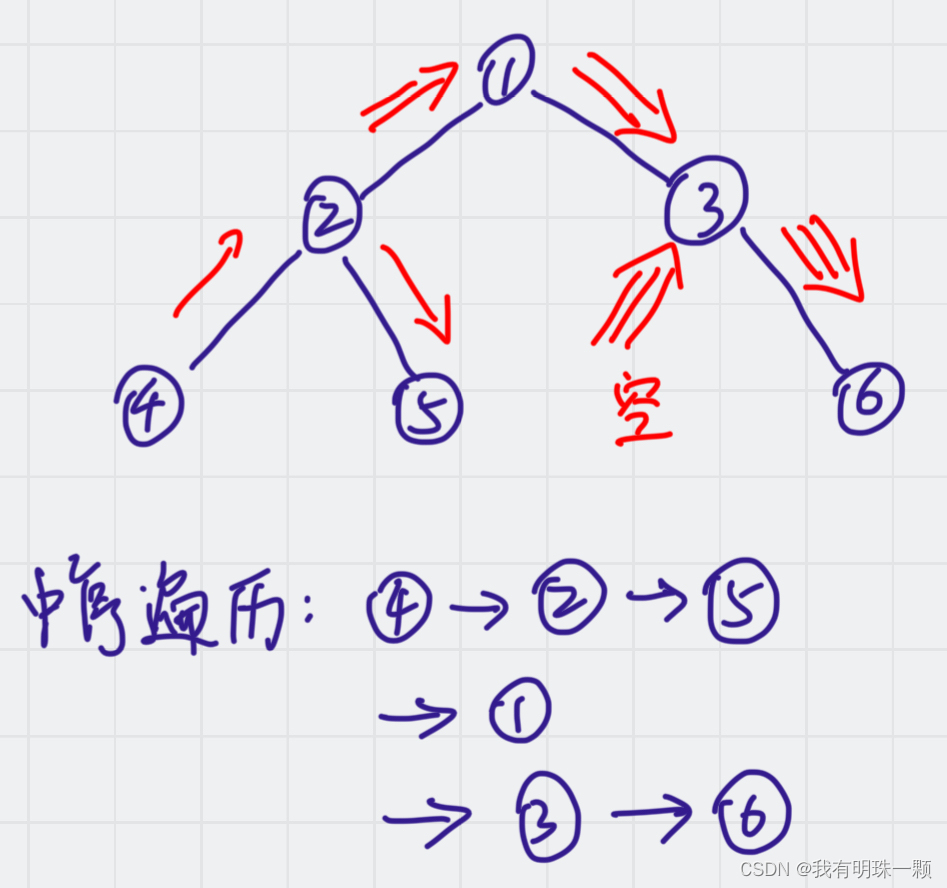
 中序遍历：左 -> 中 -> 右

练习地址：94. 二叉树的中序遍历

1、递归法 

Python实现 

# Definition for a binary tree node.
class TreeNode(object):
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right
        

class Solution(object):

    def dfs(self, root, res):
        if not root:
            return
        self.dfs(root.left, res)
        res.append(root.val)
        self.dfs(root.right, res)

    def inorderTraversal(self, root):
        res = []
        self.dfs(root, res)
        return res


if __name__ == '__main__':
    # 创建一个二叉树
    tree = TreeNode(1)
    tree.left = TreeNode(2)
    tree.right = TreeNode(3)
    tree.left.left = TreeNode(4)
    tree.left.right = TreeNode(5)
    tree.right.right = TreeNode(6)

    # 执行中序遍历
    sol = Solution()
    print(sol.inorderTraversal(tree))  # [4, 2, 5, 1, 3, 6]

Java实现

详细的测试代码请参考：算法：Java构建二叉树并递归实现二叉树的前序、中序、后序遍历-优快云博客

class Solution {
    //中序遍历
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<Integer>();
        inorder(root, res);
        return res;
    }
    public void inorder(TreeNode root, List<Integer> res) {
        if (root == null) {
            return;
        }
        inorder(root.left, res);
        res.add(root.val);
        inorder(root.right, res);
    }
}

2、迭代法

Python实现

# Definition for a binary tree node.
class TreeNode(object):
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right


class Solution(object):

    def inorderTraversal(self, root):
        res = []
        stack = []
        while root or stack:
            while root:  # 先遍历完所有左节点，放入栈中
                stack.append(root)
                root = root.left
            root = stack.pop()  # 将当前节点出栈
            res.append(root.val)
            # 将右节点作为根节点重新开始遍历，直到 root 和 栈 都为空为止
            root = root.right  
        return res


if __name__ == '__main__':
    # 创建一个二叉树
    tree = TreeNode(1)
    tree.left = TreeNode(2)
    tree.right = TreeNode(3)
    tree.left.left = TreeNode(4)
    tree.left.right = TreeNode(5)
    tree.right.right = TreeNode(6)

    # 执行中序遍历
    sol = Solution()
    print(sol.inorderTraversal(tree))  # [4, 2, 5, 1, 3, 6]

Java实现

 

class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<Integer>();
        if (root == null) {
            return res;
        }
        Deque<TreeNode> stack = new LinkedList<TreeNode>();
        TreeNode node = root;
        while(!stack.isEmpty() || node != null){
            while (node != null) {
                stack.push(node);
                node = node.left;
            }
            node = stack.pop();
            res.add(node.val);
            node = node.right;
        }
        return res;
    }
}

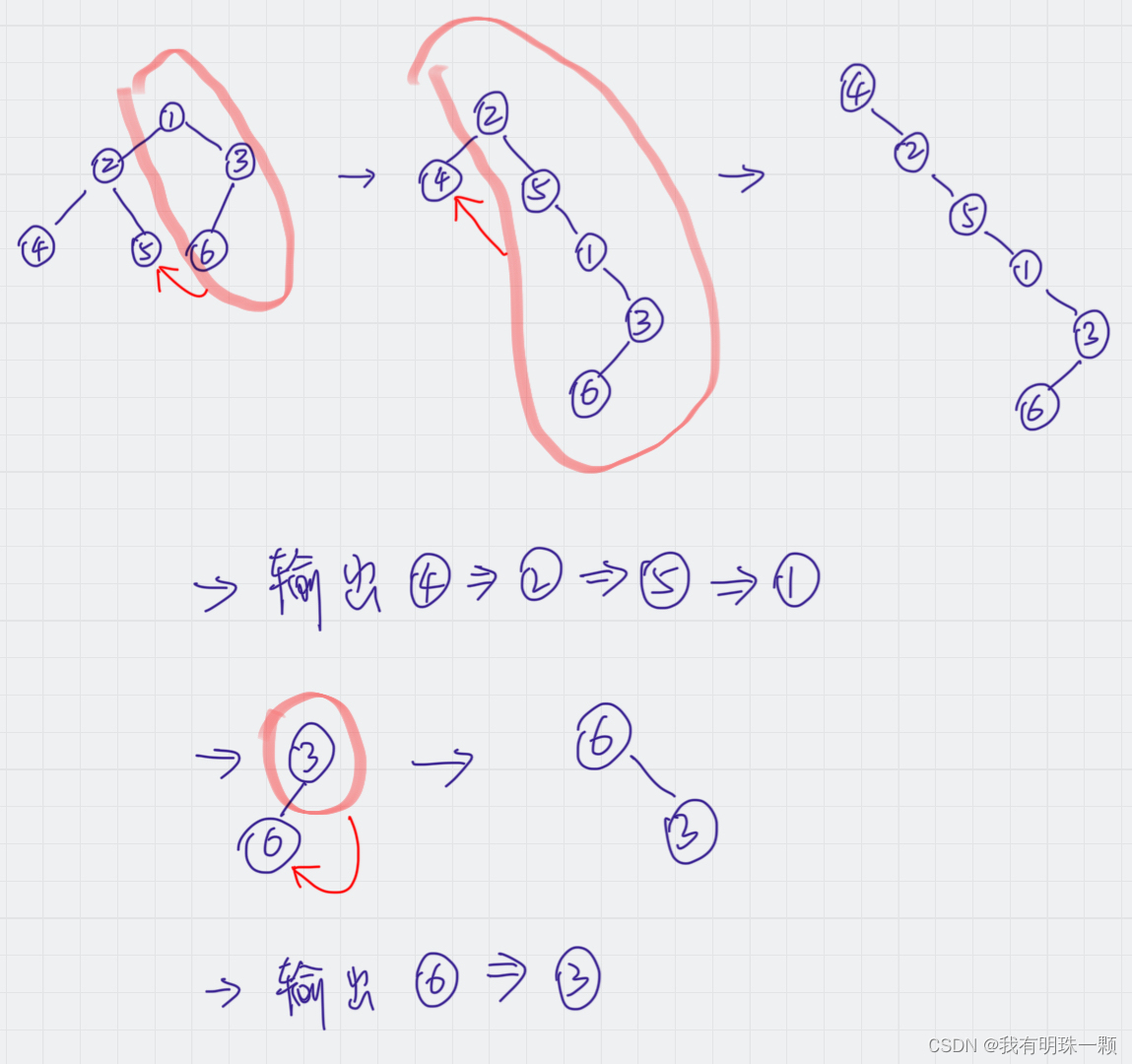
3、Morris（莫里斯）遍历法-Python

仔细看代码注释与图解，其实原理很简单。（该方法会改变树的结构）

# Definition for a binary tree node.
class TreeNode(object):
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

'''
主要思想：从上往下，把每一个节点与其右子树挂到左子树的最右边
该方法相比前两种方法，主要是节省了空间，空间复杂度从O(n)变成了O(1)
'''
class Solution(object):

    def inorderTraversal(self, root):
        res = []
        while root:
            if root.left:  # 如果当前节点存在左子树，则找到其最右边的子节点
                pre = root.left
                while pre.right:  # 找到其最右边的子节点
                    pre = pre.right
                # 把root赋值给temp，把temp的左子树设为空，挂到最右边那个子节点上去
                temp = root
                root = root.left  # 此时根结点被挂到子树上了，我们要变更根结点了，该操作不能放到 temp.left = None 后面，否则执行 temp.left = None 时 root.left 也会被置为空
                temp.left = None
                pre.right = temp
            else:
                res.append(root.val)  # 如果当前节点已经是最左边的节点了，则可以输出它的值，并开始遍历右子树了
                root = root.right
        return res


if __name__ == '__main__':
    # 创建一个二叉树
    tree = TreeNode(1)
    tree.left = TreeNode(2)
    tree.right = TreeNode(3)
    tree.left.left = TreeNode(4)
    tree.left.right = TreeNode(5)
    tree.right.left = TreeNode(6)

    # 执行中序遍历
    sol = Solution()
    print(sol.inorderTraversal(tree))  # [4, 2, 5, 1, 6, 3]

最近又看到 Morris 中序遍历的第二种解法（该方法最终不改变树的结构），提交结果很喜人，在这里分享一下代码： 

# Definition for a binary tree node.
class TreeNode(object):
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right


class Solution(object):
    def inorderTraversal(self, root):
        res = []
        while root:
            if root.left:
                tmp = root.left
                while tmp.right and tmp.right != root:
                    tmp = tmp.right
                if tmp.right is None:
                    tmp.right = root
                    root = root.left
                else:
                    pre = root
                    res.append(pre.val)
                    tmp.right = None
                    root = root.right
            else:
                pre = root
                res.append(pre.val)
                root = root.right
        return res


if __name__ == '__main__':

    # 创建一个二叉树
    tree = TreeNode(3)
    tree.left = TreeNode(1)
    tree.right = TreeNode(4)
    tree.right.left = TreeNode(2)

    # 执行中序遍历
    sol = Solution()
    print(sol.inorderTraversal(tree))  # [1, 3, 2, 4]

逻辑图： 

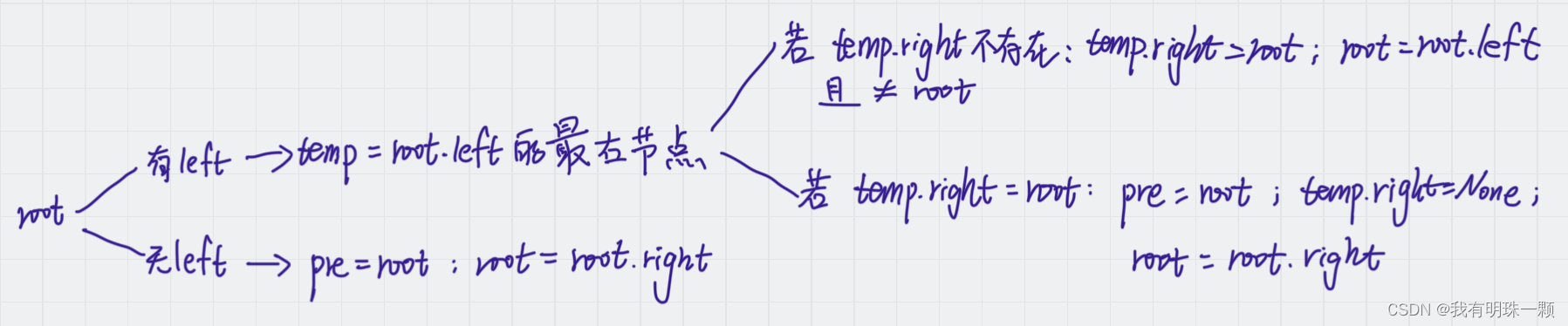
图例顺序：从左往右，从上往下 

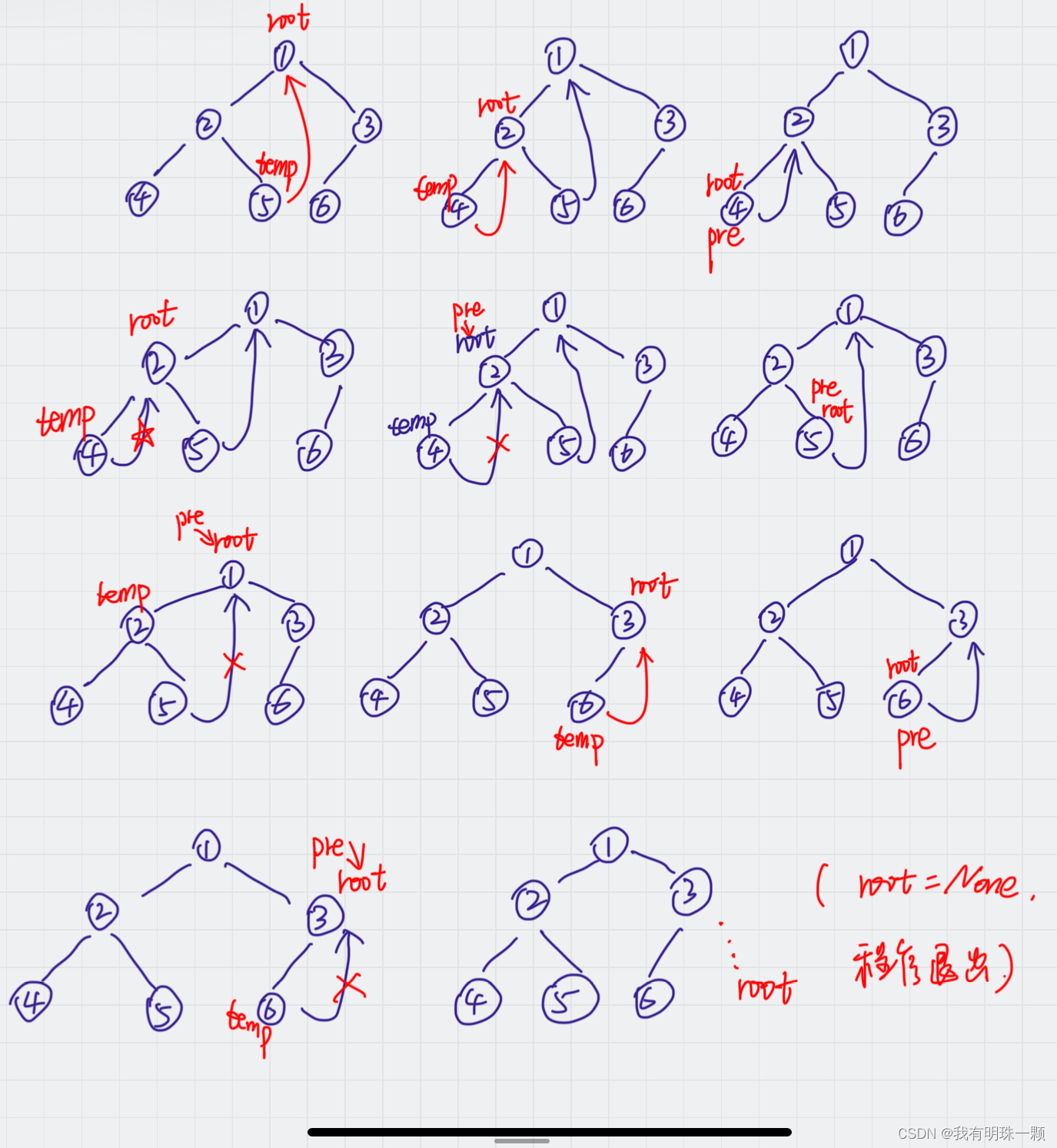 其中，pre的指向顺序就是中序遍历的节点顺序。

原理：

如果root已经是最左节点了，则输出root节点值；

如果root的左结点的右节点指向的就是root，那么则输出root节点值。

pre参数可以优化掉：

class Solution(object):
    def inorderTraversal(self, root):
        res = []
        while root:
            if root.left:
                temp = root.left
                while temp.right and temp.right != root:
                    temp = temp.right
                if not temp.right:
                    temp.right = root
                    root = root.left
                else:  # temp.right == root 的情况
                    res.append(root.val)
                    temp.right = None
                    root = root.right
            else:
                res.append(root.val)
                root = root.right
        return res