1.8 离散傅里叶变换（DFT）

1.8 离散傅里叶变换（DFT）

• 不论信号的形状如何，大多数实际关心的信号都可以看作是在不同频率下振荡的复正弦波的总和。
• 一组 NNN 个正交复正弦波可以在 NNN 个时间域样本的范围内构造。
• 离散频率轴上的每一个“刻度”或“桶”都表示该复正弦波的离散频率 k/Nk/Nk/N。

如图1.35中显示了连续时间方波，该方波是具有不同振幅的正弦波的总和。这样一个方波或矩形信号是一种被称为周期信号的特殊函数，DFT会识别出每个构成频率的幅度，例如1, 1/3, 1/5等，如方程(1.29)所示。现在让我们转向DFT的正式定义。

​​

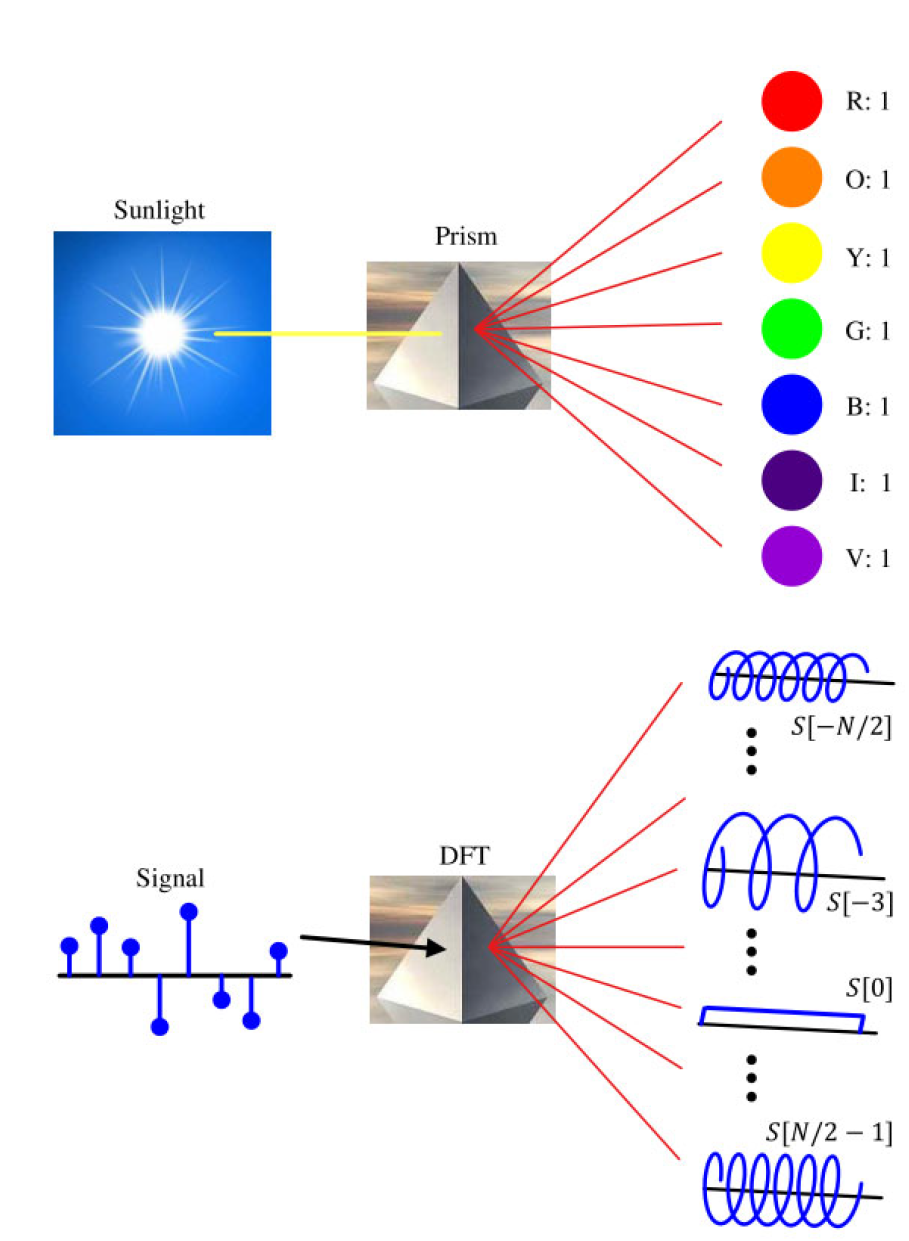
图 1.50：DFT 就像一个棱镜

定义

假设一个离散时间复正弦波被定义为 V[n]V[n]V[n]。

$$\begin{aligned} I &\rightarrow V_I[n] = \cos 2\pi \frac{k}{N} n \\ Q &\uparrow V_Q[n] = \sin 2\pi \frac{k}{N} n \end{aligned}$$

我们实际上想要做的是将一个有限长度信号 s[n]s[n]s[n] 与 NNN 个频率为 k/Nk/Nk/N 的复正弦波（在滞后0的位置上）进行相关运算。根据1.6节的相关性，将 s[n]s[n]s[n] 与复正弦波 V∗[n]V^*[n]V∗[n] 逐样相乘并取和。然后，DFT S[k]S[k]S[k] 由以下公式给出：

$$S[k] = \sum_{n=0}^{N-1} s[n] V^*[n]$$

在 s[n]s[n]s[n] 的 III 和 QQQ 分量 sI[n]s_I[n]sI​[n] 和 sQ[n]s_Q[n]sQ​[n] 的形式下，DFT S[k]S[k]S[k] 可以通过复数的乘法规则求得。

$$\begin{aligned} I &\rightarrow S_I[k] = \sum_{n=0}^{N-1} \left[ s_I[n] \cos 2\pi \frac{k}{N} n + s_Q[n] \sin 2\pi \frac{k}{N} n \right] \\ Q &\uparrow S_Q[k] = \sum_{n=0}^{N-1} \left[ s_Q[n] \cos 2\pi \frac{k}{N} n - s_I[n] \sin 2\pi \frac{k}{N} n \right] \end{aligned} \tag{1.53}$$

对每个 kkk 来说，在上面的公式中：

• kkk 是DFT输出在频域中的索引，k=−N/2,…,−1,0,1,…,N−2,N−1k = -N/2, \ldots, -1, 0, 1, \ldots, N-2, N-1k=−N/2,…,−1,0,1,…,N−2,N−1
• S[k]S[k]S[k] 是第 kkk 个DFT输出分量
• SI[k]S_I[k]SI​[k]