6.傅里叶变换2

6.傅里叶变换2

傅里叶变换的对称性

如果函数x(t)x(t)x(t)的傅里叶变换是y(f)y(f)y(f)，则y(t)y(t)y(t)的傅里叶变换是x(−f)x(-f)x(−f)。

延迟信号的傅里叶变换

若J[x(t)]=X(f)\mathscr{J}[x(t)]=X(f)J[x(t)]=X(f)，则F[x(t−t0)]=X(f)e−j2πft0\mathscr{F}[x(t-t_0)]=X(f)\mathrm{e}^{-\mathrm{j}2\pi ft_0}F[x(t−t0​)]=X(f)e−j2πft0​。时域延迟等价于频域旋转。

​​

矩形脉冲延时信号的傅里叶变换，旋转其实在三维空间里看起来形状比较怪异。

卷积

反褶：一般多项式都是按x的降幂排列，这里将其中一个多项式的各项按x的升幂排列。平移：将按x的升幂排列的多项式每次向右平移一个项。相乘：垂直对齐的项分别相乘。求和：相乘的各结果相加。

反褶、平移、相乘、求和，这就是通信原理中常用的一个概念“卷积”的计算过程。

对于两个周期信号，时域相乘相当于频域卷积。

离散序列的卷积：x[n]∗y[n]=∑k=−∞+∞x[k]y[n−k]x[n]*y[n]=\sum_{k=-\infty}^{+\infty}x[k]y[n-k]x[n]∗y[n]=∑k=−∞+∞​x[k]y[n−k]

频域卷积定理：若F[x(t)]=X(f)\mathscr{F}\left[x(t)\right]=X(f)F[x(t)]=X(f)，F[y(t)]=Y(f)\mathscr{F}[y(t)]{=}Y(f)F[y(t)]=Y(f)，则F[x(t)y(t)]=X(f)∗Y(f)\mathscr{F}[x(t)y(t)]{=}X(f){*}Y(f)F[x(t)y(t)]=X(f)∗Y(f)。。

连续函数的卷积：一般将两个离散序列的卷积称为“卷积和”，将两个连续函数的卷积称为“卷积积分”。卷积和的计算过程为：反褶—平移—相乘—求和。卷积积分的计算过程与其类似：反褶—平移—相乘—积分，只是要将最后一步“求和”改为“积分”。

$$X(f)*Y(f)=\int_{-\infty}^{+\infty}X(\tau)Y(f-\tau)\mathrm{d}\tau$$

卷积积分的计算很麻烦。值得庆幸的是：通信系统中很少用到这样的卷积积分，有一类卷积积分倒是很常用，那就是：与单位冲激函数做卷积。

一个函数与单位冲激函数的卷积结果为函数本身。一个函数​**X(f)X(f)X(f)​与单位冲激函数​δ(f−f0)δ(f-f_0)δ(f−f0​)​的卷积结果为​X(f−f0)X(f-f_0)X(f−f0​)**​ 。

​​​

频域卷积定理在调制中的应用:

​​​

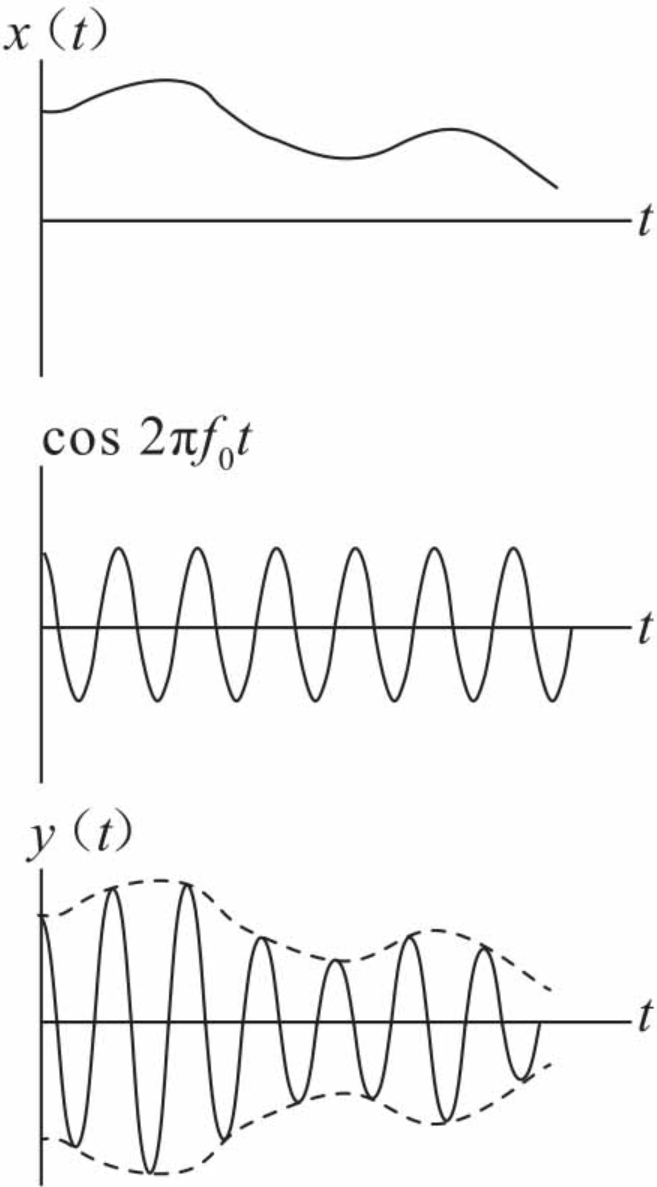
时域相乘相当于频域卷积，而cos函数在频域上为两个冲击响应，这就用到了与冲击响应的卷积，相当于频谱的搬移。这就是调制。

频域卷积定理在采样中的应用:采样就是模拟信号和抽样脉冲相乘得到抽样信号的过程

​​

​​​

在时域以TsT_sTs​为周期对信号x(t)x(t)x(t)进行采样，相当于在频域以采样频率fsf_sfs​为间隔对x(t)x(t)x(t)的频谱进行周期性拓展

信号卷积的傅里叶变换

离散系统的单位冲击响应：

如果把δ[n]δ[n]δ[n]作为输入信号输入离散系统，则对应的输出被称为单位冲激响应序列，一般用符号h[n]h[n]h[n]来表示，有了h[n]h[n]h[n]后，离散系统输入任何序列都可以得到对应的输出序列，因此常常用单位冲激响应序列​**h[n]h[n]h[n]​来描述一个离散系统**。

离散系统的输出等于输入序列和单位冲激响应序列的卷积。

连续系统的单位冲击响应：

如果把单位冲激信号δ(t)δ(t)δ(t)作为输入信号输入连续系统，则对应的输出被称为单位冲激响应，一般用符号h(t)h(t)h(t)来表示，有了h(t)h(t)h(t)后，连续系统输入任何信号都可以得到对应的输出信号，因此常常用单位冲激响应h(t)h(t)h(t)来描述一个连续系统。

连续系统的输出也是等于输入信号和单位冲激响应的卷积

为什么通过理想低通滤波器可以重建原始模拟信号呢？