C#实现贝塞尔曲线的算法

原理

首先，关于贝塞尔曲线的形成原理网上有很多详解文章。

这里给大家推荐几篇文章的连接作为参考：

1. https://www.cnblogs.com/jay-dong/archive/2012/09/26/2704188.html
2. https://blog.youkuaiyun.com/xiexian1204/article/details/49592765
3. https://pages.mtu.edu/~shene/COURSES/cs3621/NOTES/spline/Bezier/de-casteljau.html

比起文字，我觉得下面的一幅动态图更能将其原理准确的表现出来：

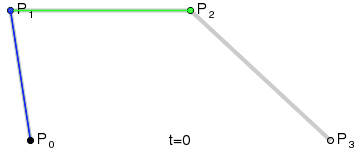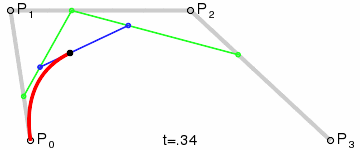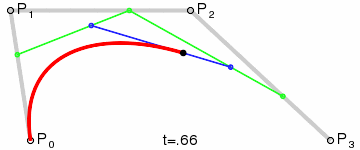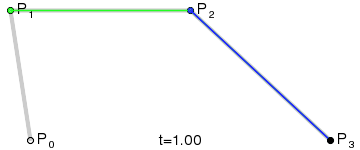
上图是4个锚点的动图，而除了4个的还可以有更多的锚点，但原理都是一样的。如图：

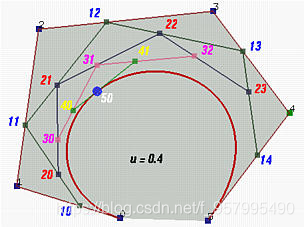
其实，锚点的个数只要大于等于3个的情况下便可以画出一条贝塞尔曲线。

代码

先根据动图中4个锚点的情况，简单的写一个贝塞尔的逻辑：

public List<Transform> gameOjbet_tran = new List<Transform>();
private List<Vector3> point = new List<Vector3>();
void Init()
{
   
   
    point = new List<Vector3>();
    for (int i = 0; i < 200; i++)
    {