精通 triton 使用 MLIR 的源码逻辑 - 第002节：再掌握一些 triton 语法 — 通过 02 softmax

Eloudy

已于 2025-07-19 18:05:25 修改

阅读量899

点赞数 13

CC 4.0 BY-SA版权

文章标签： mlir triton 编译器

于 2025-07-18 12:31:58 首次发布

本文链接：https://blog.youkuaiyun.com/eloudy/article/details/149419295

1. 热身预备向量的 softmax 函数

Softmax 函数是深度学习和机器学习中广泛使用的激活函数，主要用于多分类问题，将输入向量转换为概率分布，使得所有输出值的和为 1。

1.1. Softmax 函数原理

设 $X=[x_1,x_2, \dots , x_n]$ 则其 Softmax 函数的数学定义为，

$\text{Softmax}(x_i) = \frac{e^{x_i}}{\sum_{j=1}^n e^{x_j}}$

Softmax 函数的性质：

归一化：输出值在 [0, 1] 之间，且总和为 1，适合概率解释；

单调性：较大的输入值对应较大的输出概率；

可导性：便于反向传播优化（梯度计算）；

1.2. Softmax 计算示例

假设输入向量为 $x = [2.0, 1.0, 0.1]$

计算步骤：

step1 计算指数

$e^{2.0} \approx 7.389, \quad e^{1.0} \approx 2.718, \quad e^{0.1} \approx 1.105$

step2 求和

$\sum = 7.389 + 2.718 + 1.105 \approx 11.212$

step3 归一化：

$\text{Softmax}(x_1) = \frac{7.389}{11.212} \approx 0.659 \\ \\ \text{Softmax}(x_2) = \frac{2.718}{11.212} \approx 0.242 \\ \\ \text{Softmax}(x_3) = \frac{1.105}{11.212} \approx 0.099$

最终输出：

$\text{Softmax}(x) \approx [0.659, 0.242, 0.099]$

1.3. 矩阵逐行 Softmax 计算

在深度学习中，Softmax 通常用于矩阵（如神经网络的输出层）。通常每行代表一个样本的不同类别得分。假设输入矩阵：

$X = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ \end{bmatrix}$

可以看出矩阵 $X$ 的第一行与第二行成比例关系，所以，可以期待其对应元素的概率值也应该相等。

计算过程如下，

逐行计算 Softmax:

第一行 $[1, 2, 3]$ ：

$\text{Softmax}([1, 2, 3]) = \left[ \frac{e^1}{e^1+e^2+e^3}, \frac{e^2}{e^1+e^2+e^3}, \frac{e^3}{e^1+e^2+e^3} \right] \approx [0.090, 0.245, 0.665]$

第二行 $[4, 5, 6]$ ：

$\text{Softmax}([4, 5, 6]) \approx [0.090, 0.245, 0.665]$

最终输出矩阵:

$\text{Softmax}(X) \approx \begin{bmatrix} 0.090 & 0.245 & 0.665 \\ 0.090 & 0.245 & 0.665 \\ \end{bmatrix}$

1.4. softmax 的数值稳定性优化

由于指数计算可能导致数值溢出（exp(x) 在 x 较大时爆炸），通常采用 Log-Softmax 或减去最大值的技巧，计算结果不变：

$\text{Softmax}(x_i) = \frac{e^{x_i - \max(x)}}{\sum_j e^{x_j - \max(x)}}$

计算示例：

$x = [1000, 1001, 1002]$

直接计算 exp(1000) 会溢出，但减去 max(x)=1002 后：

$x' = [-2, -1, 0]$

再计算 Softmax：

$\text{Softmax}(x') = [ \frac{e^{-2}}{e^{-2}+e^{-1}+e^0}, \frac{e^{-1}}{e^{-2}+e^{-1}+e^0}, \frac{e^0}{...} ] \approx [0.090, 0.245, 0.665]$

1.5. 通过 python 来验证上述理论

用 Python 中的 softmax验证上述计算：

cpu 版本的 stable softmax

hello_softmax.py :


import numpy as np

def stable_softmax(x):
    x = x - np.max(x, axis=-1, keepdims=True)
    exp_x = np.exp(x)
    return exp_x / np.sum(exp_x, axis=-1, keepdims=True)



def softmax(x):
    exp_x = np.exp(x)
    return exp_x / np.sum(exp_x, axis=-1, keepdims=True)

X = np.array([[1, 2, 3], [4, 5, 6]])
print('\n softmzx X s:')
print(softmax(X))

y = np.array([500, 501, 502])
print('\n softmax y s:')
print(stable_softmax(y))

print('\n softmax y  :')
print(softmax(y))



z = np.array([1000, 1002, 1002])
print('\n softmax z s:')
print(stable_softmax(z))

print('\nsoftmax z  :')
print(softmax(z))

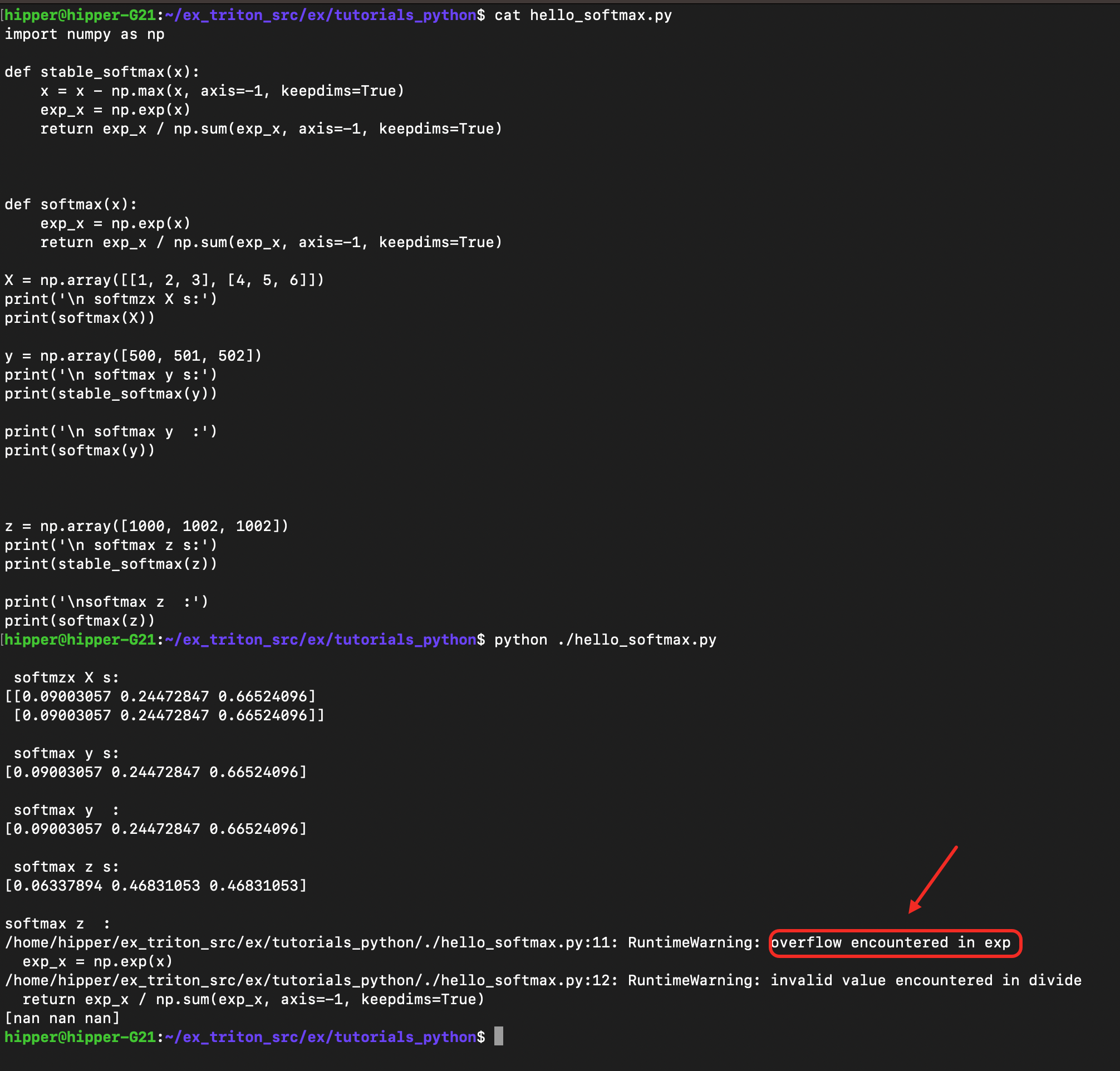
实验中可以发现，在普通的 python softmax 中，处理 [1000, 1001, 1002] 时遇到了溢出，无法顺利计算数学意义上的概率分布。

gpu 初级版本 stable softmax

naive_softmax.py :

import torch

DEVICE = torch.device("cuda" if torch.cuda.is_available() else "cpu")

def naive_softmax(x):
    x_max = x.max(dim=1)[0]
    z = x - x_max[:, None]
    numerator = torch.exp(z)
    denominator = numerator.sum(dim=1)
    ret = numerator / denominator[:, None]
    return ret

torch.manual_seed(0)
x = torch.randn(8, 8, device=DEVICE)
y_naive  = naive_softmax(x)
y_torch = torch.softmax(x, axis=1)
assert torch.allclose(y_naive, y_torch), (y_naive, y_torch)

print('y_naive =')
print(y_naive)

做点语法解释，

（1.） torch.max() 函数的基本用法
torch.max(input, dim) 函数有两个主要功能：

返回指定维度上的最大值，同时返回最大值对应的索引。
当指定 dim 参数时，它会返回一个包含两个张量的元组：
第一个张量是最大值（values）
第二个张量是最大值的索引（indices）

（2.）语法解析：x.max(dim=1)[0]

x_max = x.max(dim=1)[0]

dim=1 表示沿着第1维度（列方向）计算最大值
[0] 表示取返回元组的第一个元素（最大值张量）

运行：

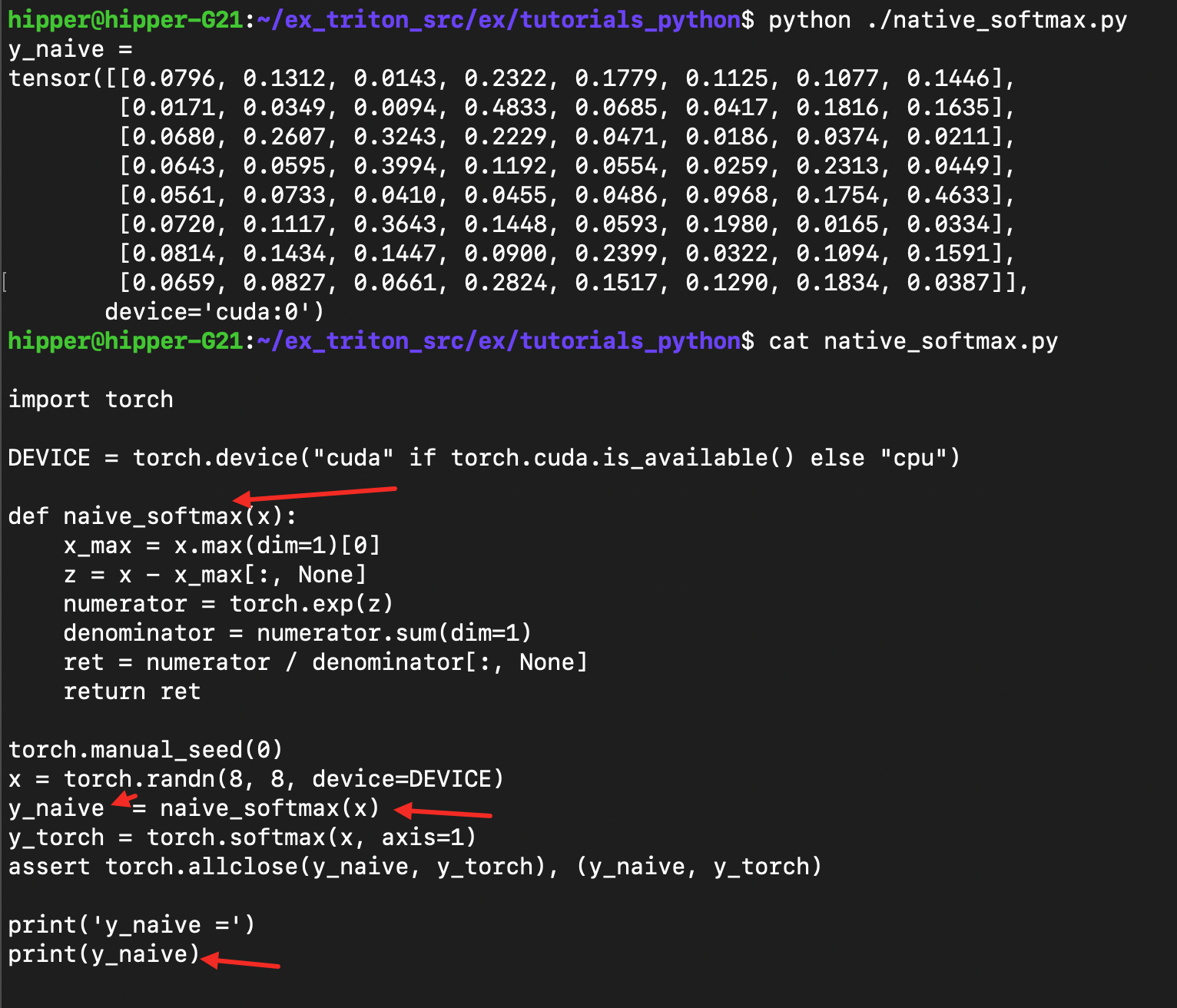
1.6. 稳定版 softmax 的简单的理论证明

Softmax 函数的定义：

$\text{Softmax}(x_i) = \frac{e^{x_i}}{\sum_{j=1}^n e^{x_j}}$

如果对输入向量 $x$ 的每个元素减去同一个常数 c，Softmax 结果不变：

$\text{Softmax}(x_i - c) = \frac{e^{x_i - c}}{\sum_{j=1}^n e^{x_j - c}} = \frac{e^{x_i} \cdot e^{-c}}{e^{-c} \cdot \sum_{j=1}^n e^{x_j}} = \frac{e^{x_i}}{\sum_{j=1}^n e^{x_j}} = \text{Softmax}(x_i)$
结论分析：

(1.) 减去任意常数 c 不影响 Softmax 的输出；

(2.) 通常选择 $c = \max(x)$ ，这样可以避免数值溢出（因为最大的指数项变为 $e^0 = 1$ .0，其他元素不大于 1.0 ）。

2. Triton 实现 stable softmax

是将 triton tutorial 02-fused-softmax.py 简化到 70行左右：

triton_stable_softmax.py :


import torch

import triton
import triton.language as tl
from triton.runtime import driver

DEVICE = triton.runtime.driver.active.get_active_torch_device()

@triton.jit
def softmax_kernel(output_ptr, input_ptr, input_row_stride, output_row_stride, n_rows, n_cols, BLOCK_SIZE: tl.constexpr,
                   num_stages: tl.constexpr):
    row_start = tl.program_id(0)
    row_step = tl.num_programs(0)
    for row_idx in tl.range(row_start, n_rows, row_step, num_stages=num_stages):
        row_start_ptr = input_ptr + row_idx * input_row_stride
        col_offsets = tl.arange(0, BLOCK_SIZE)
        input_ptrs = row_start_ptr + col_offsets
        mask = col_offsets < n_cols
        row = tl.load(input_ptrs, mask=mask, other=-float('inf'))
        row_minus_max = row - tl.max(row, axis=0)
        numerator = tl.exp(row_minus_max)
        denominator = tl.sum(numerator, axis=0)
        softmax_output = numerator / denominator
        output_row_start_ptr = output_ptr + row_idx * output_row_stride
        output_ptrs = output_row_start_ptr + col_offsets
        tl.store(output_ptrs, softmax_output, mask=mask)


properties = driver.active.utils.get_device_properties(DEVICE.index)
NUM_SM = properties["multiprocessor_count"]
NUM_REGS = properties["max_num_regs"]
SIZE_SMEM = properties["max_shared_mem"]
WARP_SIZE = properties["warpSize"]
target = triton.runtime.driver.active.get_current_target()
kernels = {}


def softmax(x):
    n_rows, n_cols = x.shape
    BLOCK_SIZE = triton.next_power_of_2(n_cols)

    num_warps = 8
    num_stages = 4 if SIZE_SMEM > 200000 else 2
    y = torch.empty_like(x)
    kernel = softmax_kernel.warmup(y, x, x.stride(0), y.stride(0), n_rows, n_cols, BLOCK_SIZE=BLOCK_SIZE,
                                   num_stages=num_stages, num_warps=num_warps, grid=(1, ))
    kernel._init_handles()
    n_regs = kernel.n_regs
    size_smem = kernel.metadata.shared

    occupancy = NUM_REGS // (n_regs * WARP_SIZE * num_warps)
    occupancy = min(occupancy, SIZE_SMEM // size_smem)
    num_programs = NUM_SM * occupancy

    num_programs = min(num_programs, n_rows)
    kernel[(num_programs, 1, 1)](y, x, x.stride(0), y.stride(0), n_rows, n_cols, BLOCK_SIZE, num_stages)
    return y


torch.manual_seed(0)
x = torch.randn(64, 64, device=DEVICE)
y_triton = softmax(x)
y_torch = torch.softmax(x, axis=1)
assert torch.allclose(y_triton, y_torch), (y_triton, y_torch)

print('y_triton =')
print(y_triton[1:16, 1:16])

先看运行结果：

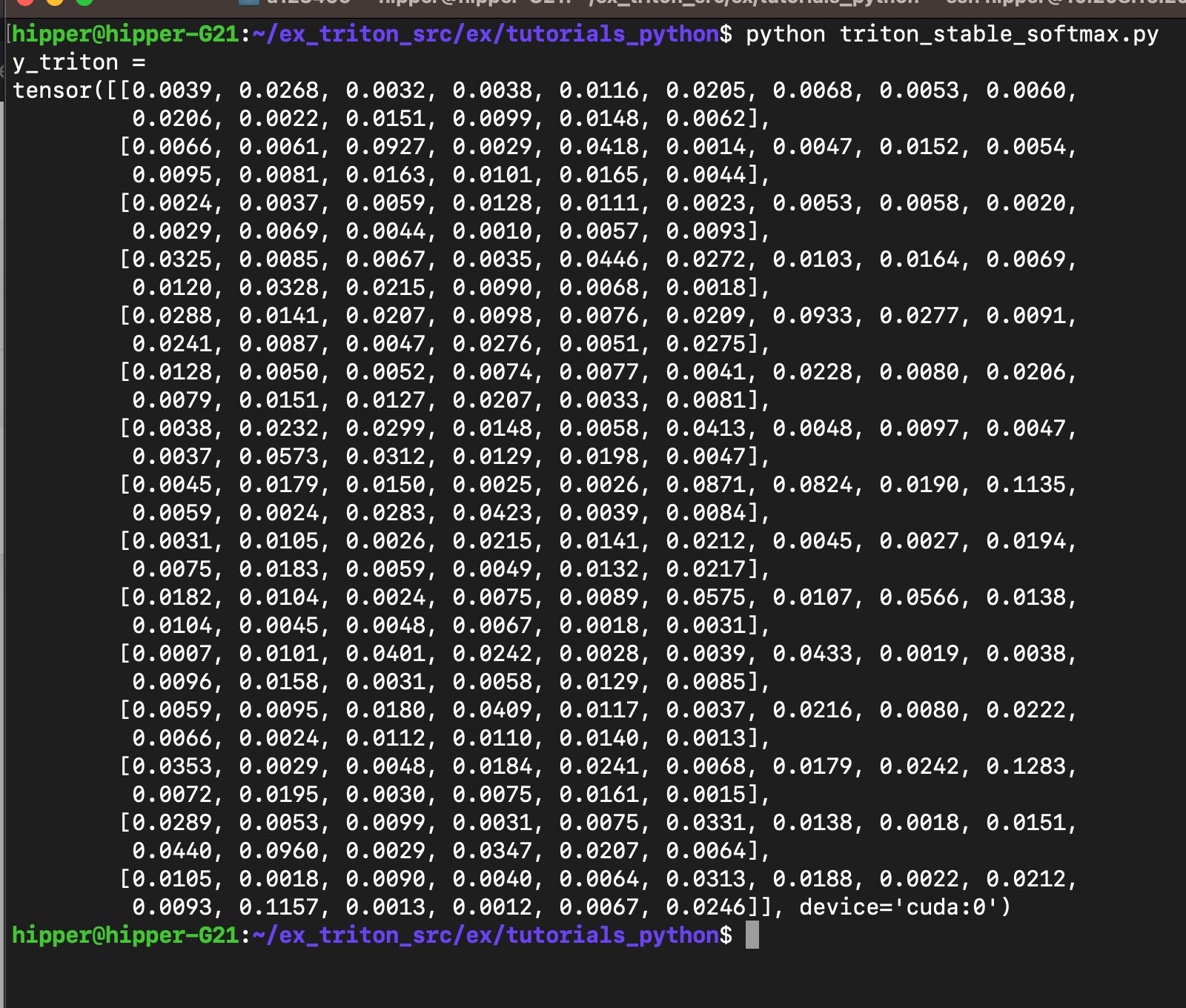
triton kernel 的逐行注释：

@triton.jit
def softmax_kernel(output_ptr,#输出矩阵指针
                   input_ptr,#输入函数指针
                   input_row_stride,#行主序的输入矩阵的 stride
                   output_row_stride,#行主序的输出矩阵的 stride
                   n_rows,#矩阵的行数
                   n_cols,#矩阵的列数
                   BLOCK_SIZE: tl.constexpr,#每一行中含 n_cols 个有效元素，block_size 为能容纳下这么多元素的一块空间长度 len，同时 len 为 2 的整数次幂。
                   num_stages: tl.constexpr):#一个指导流水线阶段数量意向值，后边展开说
    row_start = tl.program_id(0)#每个 triton 程序(类比 cuda 的 block) 每次迭代的过程中只负责矩阵一行数据的 softmax 计算。
    row_step = tl.num_programs(0)#总共能启动多少个 triton 程序，类比 cuda 的 block，也就是下一次迭代需要跨过的行数。
    #接下来这行，tl.range() 这个类似 C++ 的迭代器
    #其中特别需要指出的是 num_stages 这是一个意向值，在问题规模太大，一个就占据太多资源时，实际gpu 代码中的 stage 可能只有一个。
    for row_idx in tl.range(row_start, n_rows, row_step, num_stages=num_stages):
        row_start_ptr = input_ptr + row_idx * input_row_stride#根据自己的额 row_idx 来找到输入矩阵的一行数据的起始地址
        col_offsets = tl.arange(0, BLOCK_SIZE)#程序中的 threadIdx.x 编号构成的一维数组，即 tensor
        input_ptrs = row_start_ptr + col_offsets#本 thread 在矩阵中本行的实际取数地址
        mask = col_offsets < n_cols#边界检查用的 mask
        row = tl.load(input_ptrs, mask=mask, other=-float('inf'))#实际加载数据，此mask 彼mask;
        row_minus_max = row - tl.max(row, axis=0)#这里的 tl.max() 将会引发 reduce 操作；然后本行每个元素都会减掉本行的最大元素
        numerator = tl.exp(row_minus_max)#计算 e^{x_j}，即 softmax 中的 分子部分；
        denominator = tl.sum(numerator, axis=0)#把全部分子累加，作为 softmax 的分母
        softmax_output = numerator / denominator#计算新的元素值，即分子除以分母；
        output_row_start_ptr = output_ptr + row_idx * output_row_stride#计算回存数据行首在显存中的地址
        output_ptrs = output_row_start_ptr + col_offsets#计算本 thread 所需要存储的数据在显存中的具体地址，因线程不同而不同。
        tl.store(output_ptrs, softmax_output, mask=mask)#使用相同的掩码回存处理后的结果

2.1. triton.next_power_of_2(n_cols) 的作用

返回 $2^k$ ，其中 $k$ 为使得不等式 $2^k \ge n\_col$ 成立的最小的正整数。

2.2. _init_handles() 的作用

（1.）函数 _init_handles() 的作用

在 Triton 的 JIT 编译框架中，_init_handles() 是一个内部方法，主要用于初始化内核的底层执行句柄。_init_handles() 的主要职责是编译内核，在首次调用时，将 Triton 的 Python 代码编译为目标设备（如 GPU）的高效机器码（如 CUDA PTX）。生成优化后的计算图（DAG）和内存访问模式。分配运行时资源，为内核分配显存、流式多处理器（SM）资源等。绑定输入/输出张量的设备指针。并且做缓存管理，缓存编译后的内核二进制，避免重复编译（类似 PyTorch 的 torch.jit 缓存机制）。

（2.）设计成显式调用

在 Triton 中，内核通常通过 kernel[grid](*args) 触发隐式编译和执行。但以下场景需手动调用 _init_handles()：
预热（Warm-up）：提前编译内核，避免首次运行时因编译延迟影响性能。
参数调优：在 warmup() 后调整执行配置（如 num_warps、num_stages），需重新初始化。
低延迟场景：确保内核在关键路径前已就绪。

2.3. 执行 triton kernel

kernel[(num_programs, 1, 1)](y, x, x.stride(0), y.stride(0), n_rows, n_cols, BLOCK_SIZE, num_stages)

其他信息跟 cuda kernel 有明显的对应关系，这里借着这行代码，仅对 num_stages 多说一些。

首先，num_stages 是一个意向值（hint），指导流水线阶段数量，实际生成的 GPU 代码中 Triton 编译器会根据硬件资源限制和问题规模进行优化调整，最终可能不会完全按照设定的 num_stages 生成机器码。

2.3.1. num_stages 的原则和原理

num_stages 是编译时常量，但仅作为提示（hint）：

Triton 编译器会尝试按照 num_stages 进行流水线调度，但如果寄存器压力过大（每个 stage 需要额外的寄存器存储中间结果）或者共享内存/计算资源不足（例如 SM 上的线程块资源受限），以及当问题规模太小（如果 n_rows 很小，增加 num_stages 可能不会带来性能提升）编译器可能会自动降低 num_stages，甚至退化为 1（即无流水线）。

更具体来说，每个 stage 在流水线中需要独立的寄存器组来存储中间状态。如果 BLOCK_SIZE 很大（例如处理长向量），每个线程需要更多的寄存器，可能导致编译器被迫减少 num_stages 以避免 register spilling（寄存器溢出到全局内存，严重降低性能）。例如，在 BLOCK_SIZE=1024 且 num_stages=4 时，编译器可能会发现寄存器不够用，从而最终生成 num_stages=1 的代码。

2.3.2. 验证实际的 num_stages

Triton 提供了性能分析工具（如 triton.testing.do_bench），这样可以通过测量不同 num_stages 的性能来间接推断实际使用的阶段数。如果增加 num_stages 但性能没有提升，可能实际阶段数已被编译器优化降低。

2.3.3. 最佳实践

保守设置：通常 num_stages=3 或 4 是一个合理的起点（根据 NVIDIA GPU 的 SM 架构特性）。

资源敏感调整：如果 BLOCK_SIZE 较大，可能需要减少 num_stages。

动态适配：可以通过 triton.autotune 自动选择最优配置（Triton 内置支持自动调优）。

2.3.4. 示例场景分析

假设有以下内核：

@triton.jit
def kernel(..., BLOCK_SIZE: tl.constexpr, num_stages: tl.constexpr):
    for i in tl.range(0, n, num_stages=num_stages):
        ...

如果设置 num_stages=4 但 BLOCK_SIZE=2048（每个线程需要大量寄存器），这时 triton 编译器可能实际生成 num_stages=1 的代码，因为寄存器不足。

如果设置 num_stages=4 且 BLOCK_SIZE=128，这时编译器可能会成功生成 4 阶段流水线代码，充分利用指令级并行（ILP）。

总而言之，num_stages 是一个建议性的目标值，实际执行时 Triton 编译器会根据资源约束自动优化。理解这一点对性能调优非常重要，尤其是在处理不同规模的问题时。