小型化滤波功分器设计

功分器与低通滤波器的集成设计

摘要

本文提出了一种基于集总元件的具有谐波抑制功能的小型化滤波威尔金森功分器。该新型功分器采用两个五阶椭圆函数低通滤波器替代传统威尔金森功分器中的四分之一波长微带线。该结构将功分器与滤波器结合为一个完整器件。通过将椭圆低通滤波器与功分器集成，所提出的结构可利用滤波器的带阻特性实现对谐波的抑制。该功分器对二次谐波的测量抑制达到37.1 dB，三次谐波为36.6 dB，四次谐波为38.6 dB。在2.75至7.035 GHz范围内，谐波抑制均高于20 dB。此外，采用集总元件实现了小型化改进。与传统的功分器相比，所提出的结构有效减小了77%的尺寸。插入损耗在中心频率（1.45吉赫兹）处为3.2 分贝。

关键词 ：威尔金森功分器，低通滤波器，谐波抑制，小型化

1 引言

在现代无线通信系统中，功分器广泛应用于各种微波和毫米波电路中，例如天线阵列的馈电网络、功率放大器、混频器等。谐波抑制和微型化是功分器设计中的两个关键要求，尤其是在集成电路中。传统的威尔金森功分器由四分之一波长传输线组成，尤其在低频时占用较大的面积，并且由于其周期性，可能产生高次谐波频率响应。一种抑制这些谐波的方法是将威尔金森功分器与低通滤波器级联，但这将进一步增加电路面积和插入损耗。为了解决这些问题，已将缺陷地结构（DGS）、电磁带隙（EBG）单元、分支线结构、并联支节结构、耦合线结构、隔离电阻、FSCS单元、新型分布式阶梯阻抗谐振器网络以及正确耦合拓扑应用于功分器。然而，这些电路通常需要背面蚀刻或占用较大的尺寸。

本文提出了一种新型的小型化带谐波抑制功能的威尔金森功分器。该结构将功分器与滤波器结合为一个完整器件，与传统的功分器相比，尺寸有效减小了77%。电路仅占据14.7mm × 6.7 mm的面积。整个结构还表现出良好的谐波抑制特性，插入损耗为3.2 分贝，对二次谐波的抑制达到37.1 分贝，对三次谐波的抑制达到36.6 分贝，对四次谐波的抑制达到38.6 分贝。

2 使用集总元件的紧凑型功分器

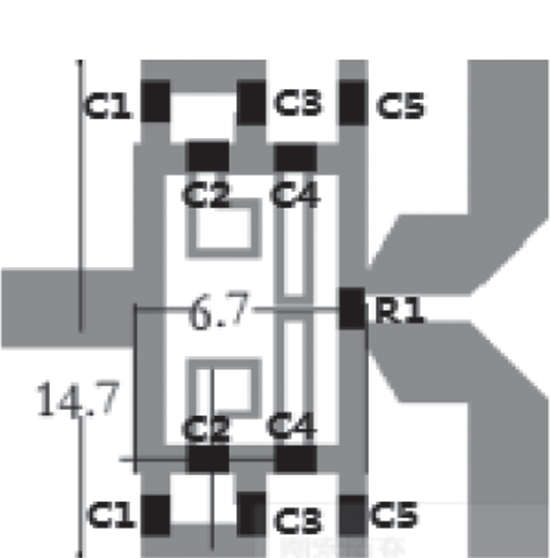
图1显示了功分器与低通滤波器的级联结构。其中zm为特性阻抗，传输线的电长度为90度。传统的功率分配器可以通过在输出端各端口添加低通滤波器来抑制谐波，但占用面积较大。

传统的功分器中的四分之一波长微带线如图2(a)所示，其中电长度为90度，zm为70.71欧姆[1, 4, 8]。提出的功率分配器的等效电路如图2(b)所示。它采用五阶椭圆低通滤波器替代了传统的四分之一波长微带线。该五阶滤波器的输入与输出之间的相位差为90度，输入输出阻抗为70.71欧姆。

传统功率分配器的四分之一波长微带线。(b) 五阶椭圆低通滤波器)

图2(b)中提出的滤波器的复合ABCD矩阵可以表示为
$$
\begin{pmatrix}
A & B \
C & D
\end{pmatrix}
=
\begin{pmatrix}
1 & 0 \
j\omega C_1 & 1
\end{pmatrix}
\begin{pmatrix}
1 & z_1 \
0 & 1
\end{pmatrix}
\begin{pmatrix}
1 & 0 \
j\omega C_3 & 1
\end{pmatrix}
\times
\begin{pmatrix}
1 & z_2 \
0 & 1
\end{pmatrix}
\begin{pmatrix}
1 & 0 \
j\omega C_5 & 1
\end{pmatrix}
\quad (1)
$$

$$
z_1 = \frac{1}{j\omega C_2} + 1 = j\omega L_1 \quad (2)
$$

$$
z_2 = \frac{1}{j\omega C_4} + 1 = j\omega L_2 \quad (3)
$$

图1(a)中四分之一波长微带线对应的ABCD矩阵可表示为
$$
\begin{pmatrix}
A & B \
C & D
\end{pmatrix}
=
\begin{pmatrix}
0 & jZ_m \
j/Z_m & 0
\end{pmatrix}
\quad (4)
$$

令(1)和(4)的ABCD矩阵相等可得
$$
C_3 = \frac{Z_m + j(z_1 + z_2)}{\omega z_1 z_2} \quad (5)
$$

$$
C_1 = \frac{1 - \omega Z_m C_3}{jZ_m z_1 \omega^2 C_3 + \omega Z_m} \quad (6)
$$

$$
C_5 = \frac{1 + j\omega z_1 C_3}{\omega^2 z_1 z_2 C_3 - j\omega(z_1 + z_2)} \quad (7)
$$

其中 $\omega$ 是角频率。提出的滤波器可以替代四分之一波长微带线。

图3显示了提出的功分器的等效电路，其中电容值为：C₁ = 0.3 pF，C₂ = 0.3 pF，C₃ = 1.1 pF，C₄ = 1 pF，C₅ = 0.2 pF，L₁ = 4.3 nH，L₂ = 3 nH。椭圆函数低通滤波器通过引入传输零点能有效抑制谐波。采用两个集总的五阶椭圆函数低通滤波器来替代传统威尔金森功分器中的四分之一波长微带线。与其他高阶或低阶滤波器相比，五阶椭圆函数低通滤波器具有相对简单的结构和良好的性能。

滤波器的相位函数可以表示为(8)。
$$
\beta(\omega) = \sum_{\text{poles}} \arctan\left(\frac{\omega - \omega_k}{\delta_k}\right) - \sum_{\text{zeros}} \arctan\left(\frac{\omega - \omega_k}{\delta_k}\right) \quad (8)
$$

其中 $\omega_k$ 和 $\sigma_k$ 是极点和零点的解。$\omega$ 是归一化频率。

图4显示了五阶滤波器的相位函数。在1.45吉赫兹时，滤波器的端口1和端口2之间的相位差为90度。通过优化电容值和电感值，椭圆函数低通滤波器和威尔金森功分器被完全集成在一起。使用四条微带线来改善相位和阻抗特性。输入与五阶滤波器输出之间的相位差为90度，且输入输出阻抗为70.71欧姆。

传统功率分配器。(b) 提出的功率分配器)

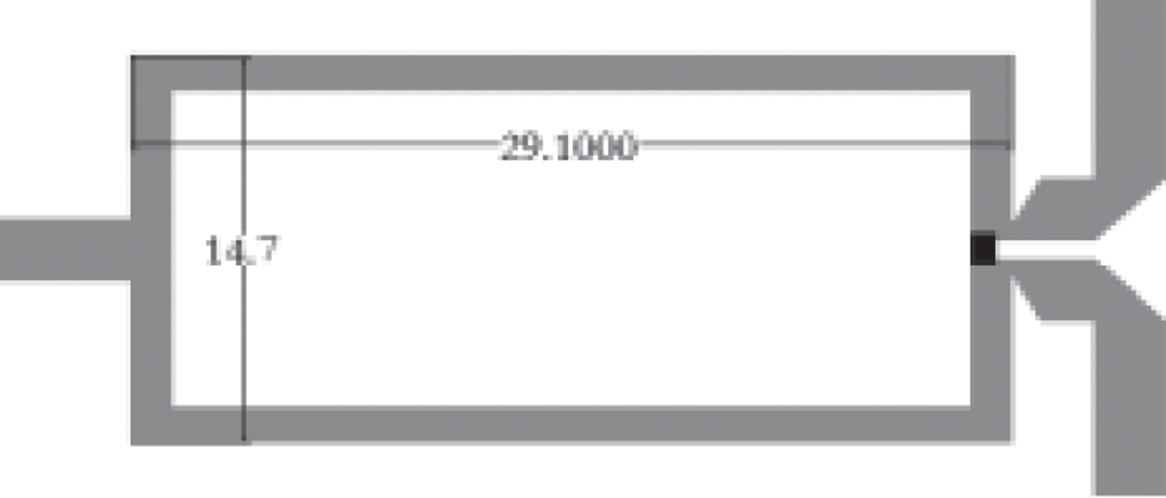
传统功分器与提出的功分器的布局在图5中进行了比较，新功分器的占用面积减少了77%。1.45 GHz威尔金森功分器的核心尺寸仅为14.7 mm × 6.7 mm（0.096λ × 0.044λ），而传统功分器的核心尺寸为14.7 mm × 29.1 mm（0.096λ × 0.189λ）。

表1：提出的功率分配器的元件值。

元件	C₁ (pF)	C₂ (pF)	C₃ (pF)	C₄ (pF)	C₅ (pF)	R₁ (ohm)
值	0.3	0.7	0.8	0.4	0.3	100

图6显示了集总功率分配器的照片。基板为泰康利 TLY-5，相对介电常数为2.2，板厚为0.76毫米。五阶滤波器的电感由宽度为0.1毫米的微带线构成。焊盘尺寸为0.8毫米 × 0.96毫米。枝节间距为0.8毫米，用于安装100欧姆隔离电阻。

S11 和 S21，(b) S22 和 S23)

提出的功分器的仿真与实测结果如图7所示。软件使用ANSYS电子桌面（HFSS）进行仿真，测量在安捷伦矢量网络分析仪上完成，网络分析仪型号为 Keysight N5245A。仿真结果表明，对二次谐波 (2.9 GHz) 的抑制达到66分贝，对三次谐波 (4.35 GHz) 的抑制为46.3分贝，对四次谐波 (5.8 GHz) 的抑制为37.9分贝，且新型功分器在2.744–6.974 GHz频带范围内对谐波的抑制均超过20分贝。仿真相对频带宽度为31.3%，中心频率（1.45 GHz），因为此时回波损耗和隔离度性能更优。

仿真值显示，在中心频率（1.45 GHz）处S21的功率分配为3.22 分贝，S11的回波损耗约为41.3 分贝，端口2与端口3之间的隔离度为43.6 分贝。而测量结果显示，二次谐波（2.9 GHz）的抑制为37.1 分贝，三次谐波（4.35 GHz）的抑制为36.6 分贝，四次谐波（5.8 GHz）的抑制为38.6 分贝。在2.75–7.035 GHz范围内，谐波抑制优于20 分贝。实测相对频带宽度为中心频率（1.45 GHz）的29.7%，因为在1.252 GHz至1.683 GHz范围内，回波损耗和隔离度均优于20 分贝。在中心频率1.45 GHz处，测量的S21显示功率分配为3.2 分贝，S11的回波损耗约为38.7 分贝，端口2与端口3之间的隔离度为36.6 分贝。

图8显示了所提出结构的仿真值和测量群时延。该群特性非常好。

表2：与现有先进水平的比较。

Name	拓扑结构	抑制 (dB)	与…相比的尺寸 传统的分隔符 (%)
[1]	DGS	−35@3f₀	34
[2]	EBG	−32.5@3f₀	70
		−12@5f₀
[3]	支路结构	−39@3f₀	50
		−52@5f₀
[4]	支路结构和并联支节结构	−40@2f₀	133.3
		−40@3f₀
		−40@4f₀
[5]	耦合线结构	−30@2f₀	40
		−20@3f₀
[6]	传输线 + 电感器 + 隔离电阻	−28@2f₀	50
		−32@3f₀
		−20@4f₀
[7]	隔离电阻	−45@2f₀	140
[8]	FSCS单元	−35@3f₀	416.7
		−40@5f₀
		−35@7f₀
[9]	新型分布式阶梯式阻抗谐振器网络	−45@2f₀	1061.3
		−40@3f₀
		−35@4f₀
		−30@5f₀
[10]	正确耦合拓扑结构	−30@2f₀	1052.5
		−40@3f₀
This work	集总结构	−37.1@2f₀	23
		−36.6@3f₀
		−38.6@4f₀

4 结论

提出了一种采用集总结构的小型化威尔金森功分器，兼具小型化和谐波抑制功能。该结构将功分器与滤波器结合为一个完整器件。使用集总元件的功分器已进行仿真和测量。小型化结构的核心占用面积已减小至传统威尔金森功分器的23%。新型功分器在2.75–7.035 GHz范围内具有良好的谐波抑制性能。测量结果显示，二次谐波抑制为37.1 分贝，三次谐波抑制为36.6 分贝，四次谐波抑制为38.6 分贝。带宽为29.7%，中心频率为1.45 GHz。所提出的结构也可应用于其他频率。