【算法简述】基础数据结构-单调队列

它的队首和普通的队列一样，只能删除元素，而它的队尾既可以添加元素也可以删除元素。 他随队尾输出，出队。

单调队列的作用&原理

就是用来维护一段区间内的单调上升，下降性质，导出性质就是也可以用来维护一个区间内的值。他的原理是这样的:
重复一遍，队列1，2，-3，-4，2.如果元素a入队，从队尾弹出所有大于a的值，再把a加紧队尾。

1. 1带入队列，为了初始化。
2. 2带入队列，因为1比2小，此时队列为1，2
3. -3代入队列，有哪位-3比1，2都小，弹出1，2，-3带入队列
4. -4带入队列，因为-4<-3,所以弹出-3，带入-4，此时为-4.
5. 2带入队列，因为2大于-4，所以，此时为2，-4.

从队尾到队首开始遍历，如果碰到元素比待入队元素要小，那么这个元素便失去了作因为维护的是最大值，如果有一个比当前值小，那它一定不是最大的，将其出队。直到碰到一个比当前值大的元素，跳出循环；

---

题目组织代码

题目描述

现在有一堆数字共N个数字（N<=10^6），以及一个大小为k的窗口。现在这个从左边开始向右滑动，每次滑动一个单位，求出每次滑动后窗口中的最大值和最小值。

例如：

The array is [1 3 -1 -3 5 3 6 7], and k = 3.

输入格式

输入一共有两行，第一行为n,k。

第二行为n个数(<INT_MAX). 输出格式

输出共两行，第一行为每次窗口滑动的最小值

第二行为每次窗口滑动的最大值 输入输出样例 输入 #1

8 3

1 3 -1 -3 5 3 6 7

输出 #1

-1 -3 -3 -3 3 3

3 3 5 5 6 7

说明/提示

50%的数据，n<=10^5

100%的数据，n<=10^6

接下来，我给大家讲一讲例子的实现过程：

1 3 -1 -3 5 3 6 7

连续三个数，所以有：
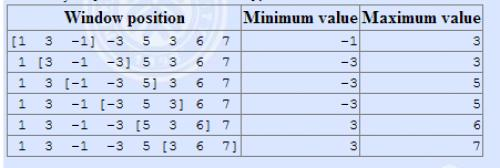
【1,3，-1】【3，-1，-3】【-1，-3，5】【-3,5,3】【5,3,6】【3,6,7】
从中选出最大和最小：
-1 -3 -3 -3 3 3
3 3 5 5 6 7

那么分析完样例——单调队列做这个题就行了

#include<bits/stdc++.h>
using namespace std;
int n,m;
int s[1000001],s2[1000001];
int a[1000001];
int minn(){
    int u=1,v=0;//u表示队头元素，v表示队尾元素
    for(int i=1;i<=n;i++){
        while(u<=v&&s[u]+m<=i) u++;//如果队尾元素大于队头元素，就如入队
        while(u<=v&&a[i]<a[s[v]]) v--;//若果队尾元素比我们要继续处理的值大，此时，队尾元素就不能入队，接下来出队
        s[v++]=i;// 存到队列
        if(i>=m) cout<<a[s[u]]<<" ";
    }
    cout<<endl;
}
int maxn(){
    int u=1,v=0;//u表示队头元素，v表示队尾元素
    for(int i=1;i<=n;i++){
        while(u<=v&&s2[u]+m<=i) u++;//如果队尾元素大于队头元素，就如入队
        while(u<=v&&a[i]>a[s2[v]]) tv-;//若果队尾元素比我们要继续处理的值大，此时，队尾元素就不能入队，接下来出队
        s2[v++]=i;// 存到队列
        if(i>=m) cout<<a[s2[u]]<<" ";
    }
}
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>a[i];
    minn();
    maxn();
    return 0;
}