【算法简述】图论专题：拓扑排序

一个问题通常会涉及多个环节，但是，环节之间是有特殊关系，有些活动在别的活动做完才能继续执行，比如，在刷题的环节时，你必须先我完成一个环节的任务，后面的环节都会有先前的要求。
这样的过程我们叫做有向无环图：

拓扑排序

基本思想：将有向无环图去掉它的约束。
找出一个满足有向无环图的满足关系的节点排列（点不受后面的约束）
以施工的流程图为例，有些活动（子工程）必须要先执行，有些活动需要在其他活动之后才可以执行。为了形象地反映出整个工程中各个活动之间的先后关系，可用一个有向图来表示，图中的顶点代表活动，图中的有向边代表活动的先后关系，即有向边的起点是终点的前序，只有当起点活动完成之后，其终点活动才能进行。

算法流程

• 把所有入度为0的点记录下来（不受约束）。

• 对于记录下来的点，去掉入读为-1的点（约束），如果某个点入读将为0，也将其记录下来。

• 反复执行上面的操作，直到记录没有这个点时（此时为一个拓排序）。

循环结束，若输出的顶点数小于图中的顶点数，则表示该图中存在回路，也就是无法进行拓扑排序；否则输出的顶点序列就是一个拓扑序列。接下来，我们用一个例子来说明这个算法过程。对于如下的图，我们首先统计所有顶点的入度，并找出其中所有入度为零的顶点，发现只有 ，于是我们将 插入队列中。

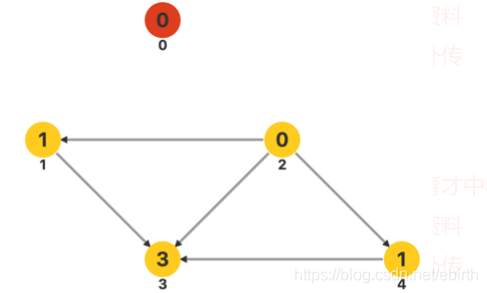
处理完成后将队首元素出队，继续访问当前的队首元素 2。

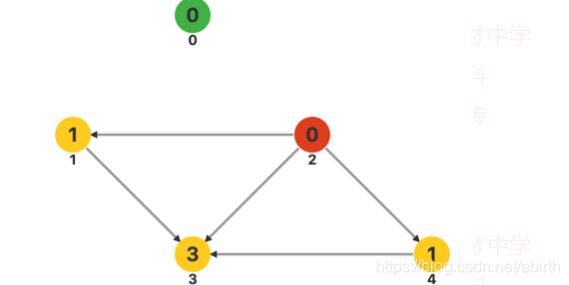
枚举 2连出的所有边，对于每条边，将另一端的顶点的入度减一。这时发现顶点 1和顶点 4的入度均为零，将它们都插入队列。

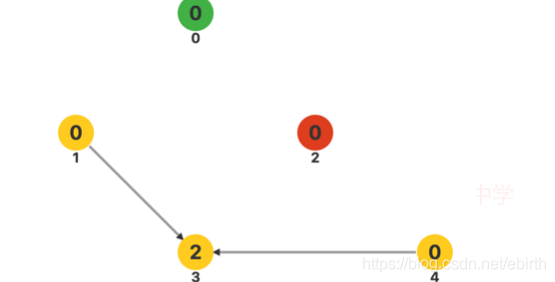
接下来的操作，我就不多讲了，以此类推。

实现代码

列题：排队

排队
描述
今天，学校老师让同学们排成一队，准备带大家出去玩，一共有 n 名同学，排队的时候同学们向老师提了 m 条要求，每一条要求是说同学 x 一定要排在同学 y 之前，老师现在想找到一种排队方式可以满足所有的要求，你能帮帮他吗？
输入
第一行两个整数 n,m(1≤n≤10^410
4
,1≤m≤10^5 )，表示同学数和要求数；
以下 m 行，每行两个整数 x,y，之间用一个空格隔开，表示某个要求是第 x 号同学要排在第 y 号同学之前，所有同学的编号由 1 开始；
输入保证有解。
输出
输出一行，包括 n 个整数，表示从前往后同学的编号，用空格隔开，如果答案不唯一，输出字典序最小的答案。
输入样例 1
2 1
1 2
输出样例 1
1 2
提示
提示：使用优先队列进行拓扑排序

#include<bits/stdc++.h>
#include<queue>
using namespace std;

const int MAX_N=20000;
const int MAX_M=200000;
int ans[20000],cnt;
struct edge{
	int v,next;
	int len;
}E[MAX_M];
int p[MAX_N],eid;
void init(){
	memset(p,-1,sizeof(p));
	eid=0;
}
void insert(int u,int v){
	E[eid].v=v;
	E[eid].next=p[u];
	p[u]=eid++;
}
int n,m;
int indegree[MAX_N];
priority_queue<int,vector<int>,greater<int> > q;
void topo(){
	//queue<int> q;
	for(int i=1;i<=n;i++){
		if(indegree[i]==0){
			q.push(i);
		}
	}
	while(!q.empty()){
		int now=q.top();
		cnt++;
		ans[cnt]=now;
		q.pop();
		for(int i=p[now];i!=-1;i=E[i].next){
			int v=E[i].v;
			indegree[v]--;
			if(indegree[v]==0){
				q.push(v);
			}
		}
	}
}
int main(){
	init();
	memset(indegree,0,sizeof(indegree));
	cin>>n>>m;
	for(int i=0;i<m;i++){
		int u,v;
		cin>>u>>v;
		insert(u,v);
		indegree[v]++;
	}
	topo();
	for(int i=1;i<=cnt;i++){
		cout<<ans[i];
		if(i<cnt){
			cout<<" ";
		}
	}
	return 0;
}