7.礼物的最大价值（medium）-优快云博客

1.题目链接：

LCR 166. 珠宝的最高价值 - 力扣（LeetCode）LCR 166. 珠宝的最高价值 - 现有一个记作二维矩阵 frame 的珠宝架，其中 frame[i][j] 为该位置珠宝的价值。拿取珠宝的规则为： * 只能从架子的左上角开始拿珠宝 * 每次可以移动到右侧或下侧的相邻位置 * 到达珠宝架子的右下角时，停止拿取注意：珠宝的价值都是大于 0 的。除非这个架子上没有任何珠宝，比如 frame = [[0]]。示例 1：输入：frame = [[1,3,1],[1,5,1],[4,2,1]]输出：12解释：路径 1→3→5→2→1 可以拿到最高价值的珠宝提示： * 0 < frame.length <= 200 * 0 < frame[0].length <= 200 https://leetcode.cn/problems/li-wu-de-zui-da-jie-zhi-lcof/description/

2.题目描述：

在一个 m*n 的棋盘的每一格都放有一个礼物，每个礼物都有一定的价值（价值大于 0）。你可以从棋盘的左上角开始拿格子里的礼物，并每次向右或者向下移动一格、直到到达棋盘的右下角。给定一个棋盘及其上面的礼物的价值，请计算你最多能拿到多少价值的礼物？

     示例 1:
     输入:
     [
     [1,3,1],
     [1,5,1],
     [4,2,1]
     ]
     输出: 12
     解释: 路径 1→3→5→2→1 可以拿到最多价值的礼物3. 解法（动态规划）：
算法思路：
1. 状态表示：

对于这种「路径类」的问题，我们的状态表示一般有两种形式：

i.	从 [i, j] 位置出发，巴拉巴拉；

ii. 从起始位置出发，到达 [i, j] 位置，巴拉巴拉。

这里选择第二种定义状态表示的方式：

dp[i][j] 表示：走到 [i, j] 位置处，此时的最大价值。

2. 状态转移方程：

对于 dp[i][j] ，我们发现想要到达 [i, j] 位置，有两种方式：


i.	从 [i, j] 位置的上方 [i - 1, j] 位置，向下走一步，此时到达 [i, j] 位置能

拿到的礼物价值为 dp[i - 1][j] + grid[i][j] ；

ii. 从 [i, j] 位置的左边 [i, j - 1] 位置，向右走一步，此时到达 [i, j] 位置能

拿到的礼物价值为 dp[i][j - 1] + grid[i][j]

我们要的是最大值，因此状态转移方程为：

dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]) + grid[i][j] 。

3. 初始化：

可以在最前面加上一个「辅助结点」，帮助我们初始化。使用这种技巧要注意两个点：

i. 辅助结点里面的值要「保证后续填表是正确的」；

ii. 「下标的映射关系」。

在本题中，「添加一行」，并且「添加一列」后，所有的值都为 0 即可。

4. 填表顺序：

根据「状态转移方程」，填表的顺序是「从上往下填写每一行」，「每一行从左往右」。

5. 返回值：

根据「状态表示」，我们应该返回 dp[m][n] 的值。

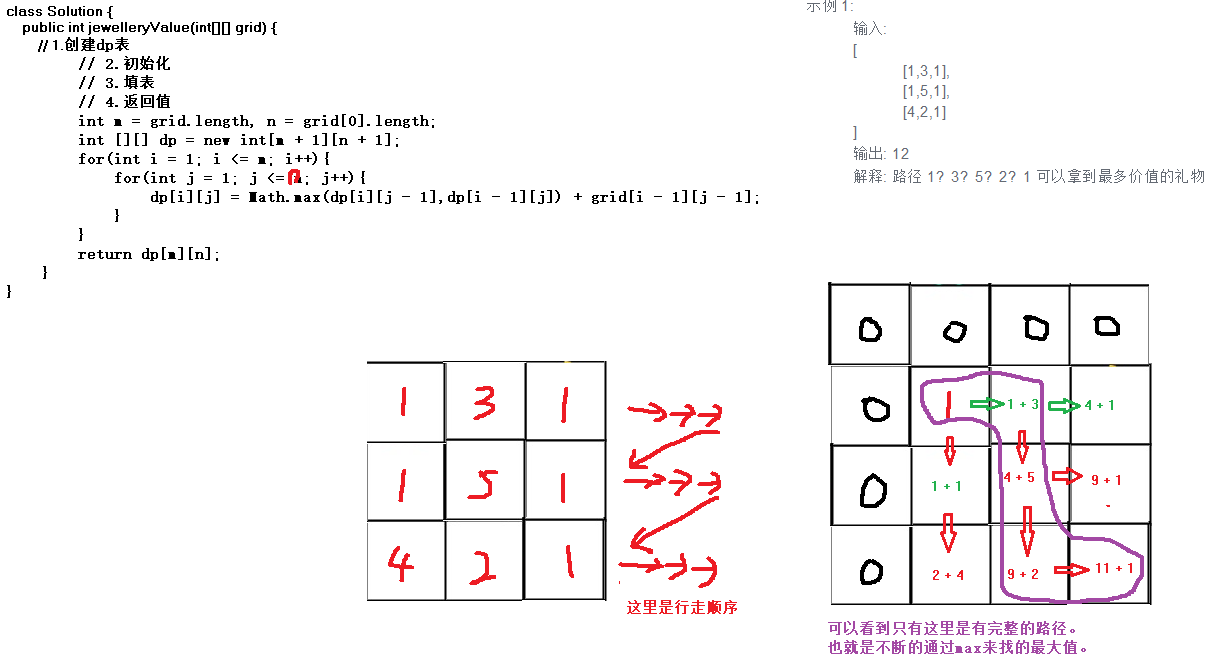
Java算法代码：

class Solution {
    public int jewelleryValue(int[][] grid) {
        // 1.创建dp表
        // 2.初始化
        // 3.填表
        // 4.返回值
        int m = grid.length, n = grid[0].length;
        int [][] dp = new int[m + 1][n + 1];
        for(int i = 1; i <= m; i++){
            for(int j = 1; j <= m; j++){
                dp[i][j] = Math.max(dp[i][j - 1],dp[i - 1][j]) + grid[i - 1][j - 1];
            }
        }
        return dp[m][n];
    }
}

执行结果：

动态规划：