8.下降路径最小和（medium）

1.题目链接：

2.题目描述：

给你一个 n x n 的方形整数数组 matrix ，请你找出并返回通过 matrix 的下降路径的最小和 。​

下降路径可以从第一行中的任何元素开始，并从每一行中选择一个元素。在下一行选择的元素和当前

行所选元素最多相隔一列（即位于正下方或者沿对角线向左或者向右的第一个元素）。具体来说，位

置 (row, col) 的下一个元素应当是 (row + 1, col - 1)、(row + 1, col) 或者 (row + 1, col + 1) 。​

示例 1：​

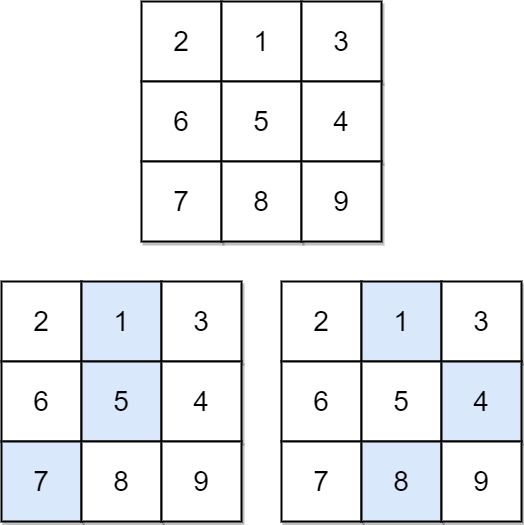
           输入：matrix = [[2,1,3],[6,5,4],[7,8,9]]​
           输出：13​
解释：
           如图所示，为和最小的两条下降路径
示例 2：​

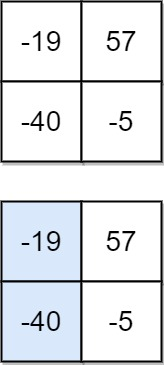
               输入：matrix = [[-19,57],[-40,-5]]​
               输出：-59​
     解释：
               如图所示，为和最小的下降路径
3. 解法（动态规划）：
算法思路：
关于这一类题，由于我们做过类似的，因此「状态表示」以及「状态转移」是比较容易分析出来的。比较难的地方可能就是对于「边界条件」的处理。

1. 状态表示：
        对于这种「路径类」的问题，我们的状态表示一般有两种形式：

i.	从 [i, j]  位置出发，到达目标位置有多少种方式；​

  ii. 从起始位置出发，到达 [i, j]  位置，一共有多少种方式​这里选择第二种定义状态表示的方式：
dp[i][j]  表示：到达 [i, j]  位置时，所有下降路径中的最小和。​

2. 状态转移方程：
        对于普遍位置 [i, j]  ，根据题意得，到达 [i, j]  位置可能有三种情况：​

i.	从正上方 [i - 1, j]  位置转移到 [i, j]  位置；​

ii. 从左上方 [i - 1, j - 1]  位置转移到 [i, j]  位置；​

iii. 从右上方 [i - 1, j + 1]  位置转移到 [i, j]  位置；​
我们要的是三种情况下的「最小值」，然后再加上矩阵在 [i, j]  位置的值。​

于是dp[i][j] = min(dp[i - 1][j], min(dp[i - 1][j - 1], dp[i - 1][j +

1])) + matrix[i][j] 。

3. 初始化：
        可以在最前面加上一个「辅助结点」，帮助我们初始化。使用这种技巧要注意两个点：                i.       辅助结点里面的值要「保证后续填表是正确的」；
                 ii. 「下标的映射关系」。

在本题中，需要「加上一行」，并且「加上两列」。所有的位置都初始化为无穷大，然后将第一行初始化为 0  即可。​

4. 填表顺序：
        根据「状态表示」，填表的顺序是「从上往下」。

5. 返回值：
注意这里不是返回 dp[m][n]  的值！​
题目要求「只要到达最后一行」就行了，因此这里应该返回「 dp 表中最后一行的最小值」。

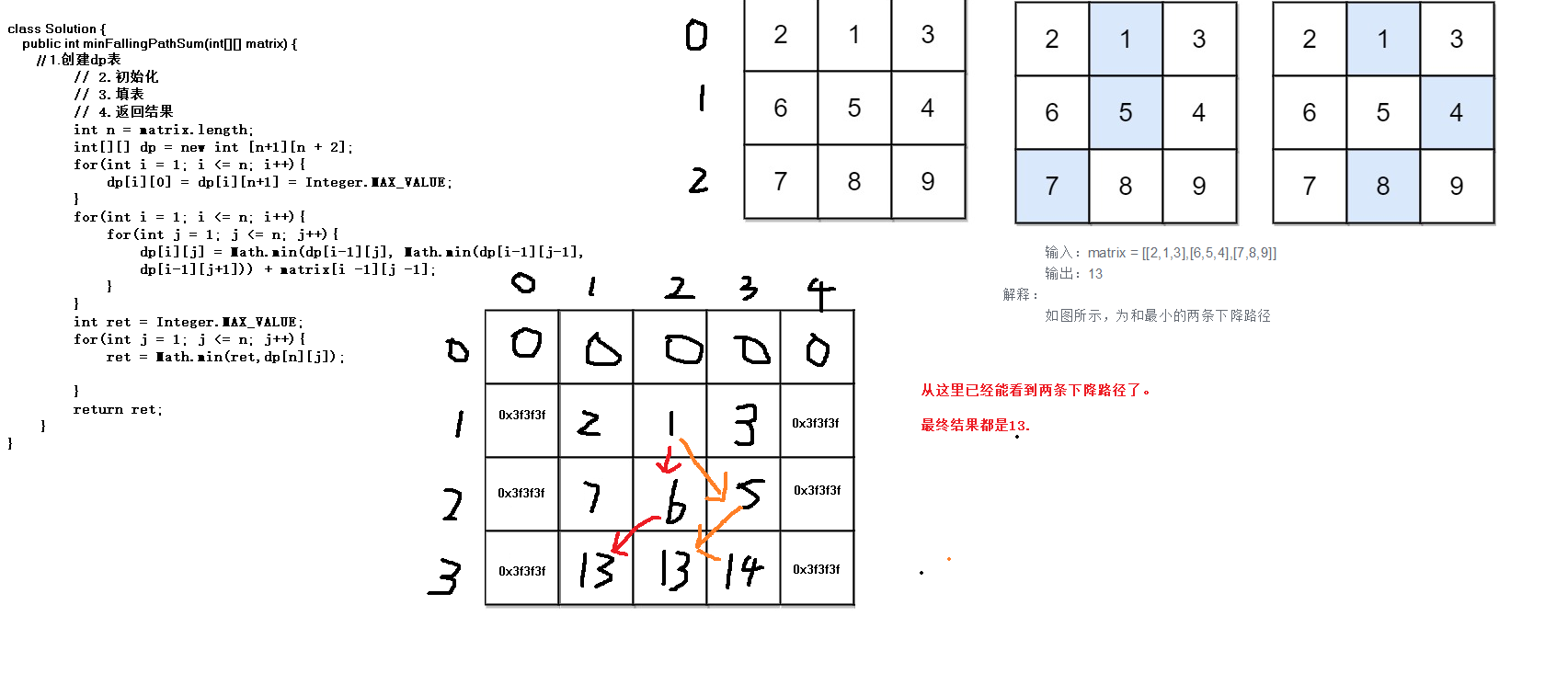
Java算法代码：

class Solution {
    public int minFallingPathSum(int[][] matrix) {
        // 1.创建dp表
        // 2.初始化
        // 3.填表
        // 4.返回结果
        int n = matrix.length;
        int[][] dp = new int [n+1][n + 2];
        for(int i = 1; i <= n; i++){
            // dp[i][0] = dp[i][n+1] = Integer.MAX_VALUE;
            dp[i][0] = dp[i][n+1] = 0x3f3f3f;

        }
        for(int i = 1; i <= n; i++){
            for(int j = 1; j <= n; j++){
                dp[i][j] = Math.min(dp[i-1][j], Math.min(dp[i-1][j-1],
                dp[i-1][j+1])) + matrix[i -1][j -1];
            }
        }
        // int ret = Integer.MAX_VALUE;
        int ret = 0x3f3f3f;

        for(int j = 1; j <= n; j++){
            ret = Math.min(ret,dp[n][j]);
        
        }
        return ret;
    }
}

运行结果：

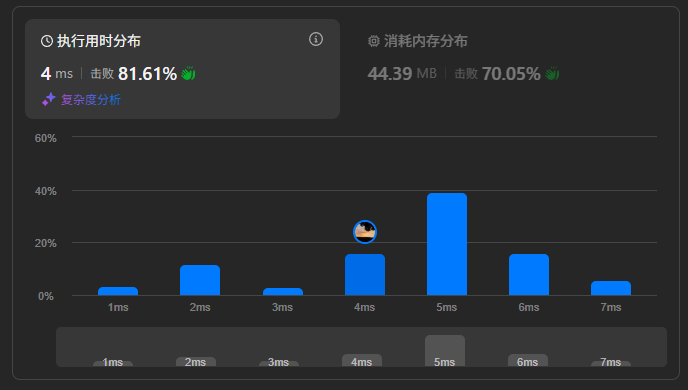
动态规划：