1.题目链接:
括号。设计一种算法,打印n对括号的所有合法的(例如,开闭一一对应)组合。 说明:解集不能包含重复的子集。
• 例如:
给出 n = 3,生成结果为:
[
"((()))",
"(()())",
"(())()",
"()(())",
"()()()"
]
3. 解法:
算法思路:
从左往右进行递归,在每个位置判断放置左右括号的可能性,若此时放置左括号合理,则放置左括号继续进行递归,右括号同理。
一种判断括号是否合法的方法:从左往右遍历,左括号的数量始终大于等于右括号的数量,并且左括号的总数量与右括号的总数量相等。因此我们在递归时需要进行以下判断:
1. 放入左括号时需判断此时左括号数量是否小于字符串总长度的一半(若左括号的数量大于等于字符 串长度的一半时继续放置左括号,则左括号的总数量一定大于右括号的总数量);
2. 放入右括号时需判断此时右括号数量是否小于左括号数量。
递归函数设计:void dfs(int step, int left)
参数:step(当前需要填入的位置),left(当前状态的字符串中的左括号数量);返回值:无;
函数作用:查找所有合理的括号序列并存储在答案列表中。
递归函数参数设置为当前状态的字符串长度以及当前状态的左括号数量,递归流程如下:
1. 递归结束条件:当前状态字符串长度与 2*n 相等,记录当前状态并返回;
2. 若此时左括号数量小于字符串总长度的一半,则在当前状态的字符串末尾添加左括号并继续递归, 递归结束撤销添加操作;
3. 若此时右括号数量小于左括号数量(右括号数量可以由当前状态的字符串长度减去左括号数量求 得),则在当前状态的字符串末尾添加右括号并递归,递归结束撤销添加操作;
Java算法代码:
class Solution {
int left, right,n;
StringBuffer path;
List<String> ret;
public List<String> generateParenthesis(int _n) {
n = _n;
path = new StringBuffer();
ret = new ArrayList<>();
dfs();
return ret;
}
public void dfs(){
if(right == n){
ret.add(path.toString());
return;
}
if(left < n) { //添加左括号
path.append('(');left++;
dfs();
path.deleteCharAt(path.length() - 1); left --;
}
if(right < left){
path.append(')');right++;
dfs();
path.deleteCharAt(path.length() - 1); right --;
}
}
}运行结果: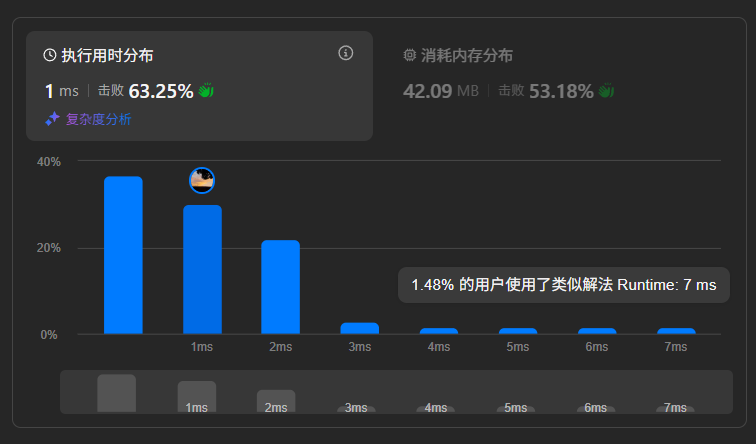
递归展开:
从做的那么多题中,慢慢得到经验,发现,越难以理解的,需要展开的阅读(也就是要知道的细节更多,才会知道递归函数怎么做的)。这里我只是展开了一小部分,就明白了。后面直接笔者就写出来了运行结果。
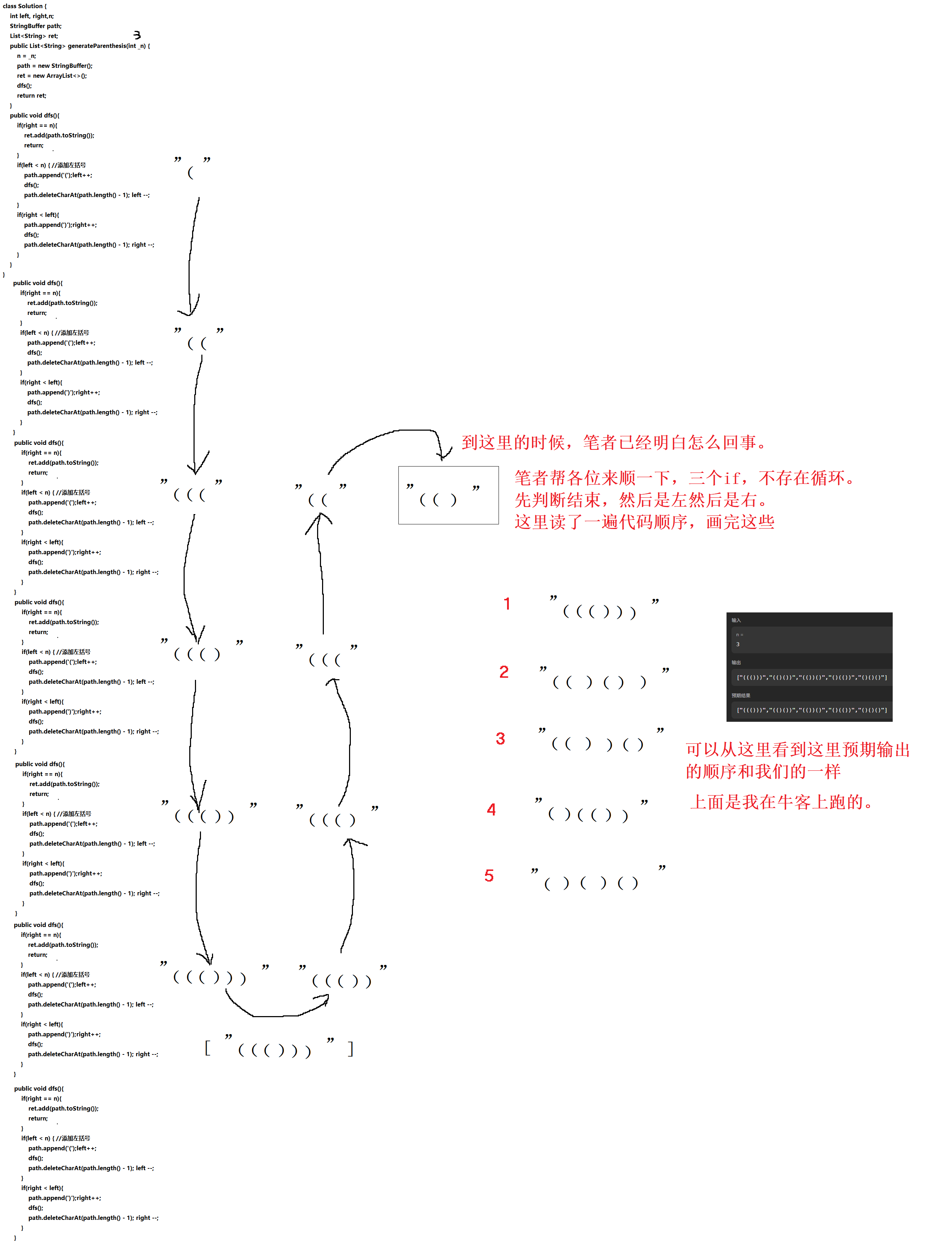
逻辑展开:
这次的逻辑展开,我认为主要是看这里(这次递归函数是三个if的格式)。
也就意味着顺序执行(只要条件满足就执行)。
1、这里三个左括号都在前面(因为左括号在右括号前面判断),这条逻辑走到黑(后面的递归,只能走右括号-----所以得到了情况1 .
2、然后1结束后,回退,这个时候,第二个左括号所在的if跳出来,然后执行右括号逻辑,添加右括号,然后再次进入递归,发现左括号小于3,然后,情况2就出来了。
3、这里到三的时候,回退最后一个左括号后,继续执行下面右括号,然后递归,然后3就出来了。
我这里简单描述三个,实际上有点难以描述(那位读者描述的更清楚,可以教教笔者)。
如果,面对面,指着说,其实会容易很多。

---------------------------------------------------------------------------------------------------------------------------------
记住,相信你的递归函数,它可以做到!
记住,不理解时候,去尝试手动展开!
记住,逻辑展开(你不可能对所有的题目都进行手动展开)!
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








