【深度学习】积累与发现

以分类为例，深度学习模型是在输入特征的基础上，经过非线性变换将特征映射到输出层维度的空间的计算过程，本质上是相当于在输入空间中寻找一个曲面（非线性变换导致），曲面分割了不同的类，只不过是通过梯度下降的方法，自动学习这个曲面。相较于传统机器学习，传统的机器学习均为固定了这个曲面的形式，例如svm就是一个超平面，logistics回归也是一个超平面。因此深度学习的学习和拟合能力更强。
但深度学习最大的两个问题：

1. 学习能力太强了，更糟的是如果数据数量不足无法代表全局数据的话，很容易过拟合，所以要使用各种手段压制模型的拟合能力，例如pooling，例如正则化；
2. 陷入局部最优，于是有了各种梯度下降的启发式算法。

神经网络基础

优化方法

深度学习基础（三）——优化算法
梯度方向是增长最快，负梯度是下降最快
优化算法
动量法：其实就是用的梯度的滑动平均值，从而保证梯度的平滑，文中的例子我觉得不太好。简单说就是如果只考虑当前梯度，那如果梯度在某个方向来回震荡，一会儿正1000，一会儿-1000，那就非常难以拟合下去，动量法就可以保证用的梯度尽量和之前的梯度方向相同
Adagrad：计算一个累计项，就是各个梯度方向的平方的和，然后用这个平方和做分母，平方和太大的方向，进行下一步的梯度步幅稍微小一点，平方和一直太小的方向，下一步的步幅稍微大点
RMSprop：把平方和换成了梯度平方的滑动平均值，就是把和换成了平均值
Adadelta：把手动输入的学习率自动运算
Adam：之前乘的都是直接是梯度，现在不了，乘梯度的滑动平均值，其余RMSPROP一样

深度学习 - 常用优化算法
什么是指数加权平均、偏差修正？
理解滑动平均(exponential moving average)
消除不稳定的随机因素，并且用不着存全部的平均值，对全体平均值的一个近似，那么为啥bachnorm用滑动平均，weight就没用滑动平均呢，我想应该是因为weight在梯度下降的时候有学习率来保障，本来学习率就不大，而且现在学习率都在下降，weight下降得本身并不快，本来最终已经到极值点了，一旦用了滑动平均，有可能反过来导致最终的模型欠拟合。

小白都能看懂的softmax详解
前馈神经网络与反向传播算法（推导过程）
$\odot$指的应该是两个形状相同的向量，把位置相同的项进行乘积

A Step by Step Backpropagation Example
详解机器学习中的梯度消失、爆炸原因及其解决方法
tanh的导数取值范围更广

【深度学习】深入理解Batch Normalization批标准化
Batch Normalization原理与实战 - 天雨粟的文章 - 知乎
主要作用是稳定训练过程（克服covariate shift）以及加速训练（将数据拉回非激活区）
对于过拟合的解释：关键在于模型必须是一个batch一个batch训练的，如果不同batch的分布不同，模型要去拟合各个batch，这个模型就会很难稳定，因为它每次都在尝试拟合每个batch，导致过拟合，所以就需要让每个batch的数据的分布都保持一致，这也是为什么不能直接用整体数据的均值和方差，因为这样导致每个batch可能仍然不是正态分布的。
bn也相当于一种data augmentation，同样的数据在不同batch中会被变化成不同的值。

BatchNormalization、LayerNormalization、InstanceNorm、GroupNorm、SwitchableNorm总结
BN在对每个样本的相同维度进行归一化，LN是对单个样本（输入）进行归一化；举例来讲，以图片为例，BN是对一个batch里的所有样本的C里的所有值求均值方差，然后作用于C；LN是对一张图片里的CHW求均值，然后作用于CHW
在RNN里，同一批batch的序列长度不一致，这个就没法bn
在AlexNet中LRN 局部响应归一化的理解
深度学习的局部响应归一化LRN(Local Response Normalization)理解
由公式可以看出，如果某个点的值很大，那么其周围通道的值就会变小
为什么不对偏置做正则化
其实不对= =偏置也能正则化，tf里有实现的，只不过习惯来讲不对bias正则化

损失函数

机器学习中的基本问题——log损失与交叉熵的等价性
深度学习系列之Focal Loss个人总结
实际是在让每个样本的损失是动态的，假设$y^{\prime }$是正样本的概率，根据式子$-(1-y^{\prime }{)}^{r}log{y}^{\prime }$可知，一个$y^{\prime }$很大的样本贡献的损失很小，也就是说已经能够被很好的分类的样本贡献的损失小，反过来就是，不容易被判别的样本贡献的损失大；对于负样本同样道理
理解交叉熵(cross_entropy)作为损失函数在神经网络中的作用
因为神经网络在多分类问题中，类标号使用的是类似于独热编码，比如某个样本是第二类，那他的期望输出就是$(0,1,0,...,0)$，所以交叉熵可以写成$L=-{\sum }_k{t}_k\cdot lnP(y=k)$
总体损失用求和值还是均值呢？我认为应该用均值，并且多数情况下也是这样的，举例来讲，对$y_1=x^2$和$y_2=3x^2$做梯度下降，当$x=1$，学习率为1的时候，那么对于$y_1$来讲，其下一个x值就是-1，而对于$y_2$来讲，其下一个x值就是-5，那么$y_2$永远也下降不下来，而对损失求和就类似于$y_2$，会导致损失函数有很多谷。
设损失函数为$loss(y,\hat{y})$，假设当前batch下的样本数量为m，特征维度为n，要更新的某个参数为$w_k\in \theta ,\theta \in R^l$，那么新的参数应该为
$$w_k:=w_k-\eta (\frac{1}{m}\sum _{i=1}^m\frac{\partial loss(y_i,{\hat{y}}_i)}{\partial {\hat{y}}_i}\frac{\partial {\hat{y}}_i}{\partial w_k}+2\lambda w_k)$$
可以先求出$\frac{\partial loss(Y,\hat{Y})}{\partial \hat{Y}}$这个$m$维列向量，向量中的第$i$个元素就是$\frac{\partial loss(y_i,{\hat{y}}_i)}{\partial {\hat{y}}_i}$
然后再求出$\frac{\partial \hat{Y}}{\partial \theta }$这个$m\ast l$的Jacobian矩阵，其中第$i$行$k$列的元素为$\frac{\partial y_i}{\partial w_k}$
于是更新权重的时候，可以利用广播性质将 $\frac{\partial loss(Y,\hat{Y})}{\partial \hat{Y}}\ast \frac{\partial \hat{Y}}{\partial \theta }$，即按列相乘，计算出来一个$m\ast l$的矩阵，其中第$i$行$k$列的元素就是$\frac{\partial loss(y_i,{\hat{y}}_i)}{\partial {\hat{y}}_i}\frac{\partial {\hat{y}}_i}{\partial w_k}$
再对每一列求平均，就得到了参数的梯度向量

激活神经元

常用的激活函数对比
常见激活函数，及其优缺点 - 面试篇
Deep learning：四十五(maxout简单理解)
激活函数(ReLU, Swish, Maxout)
不想解释了，文章写得挺明白的了，maxout的当前层的参数变成了三维的，可以看做原本的一个神经元，又拆成了一个小的前馈神经网络层，不过文中定义W的方式有点别扭
另外tanh相对于sigmoid的优点2，这块需要回想一下BP算法，在BP算法里，反向传播的时候用到了下一层神经元的输出，而sigmoid的输出恒正，tanh的输出有正负，可取的值范围变大了，因此梯度的范围也变大了，从而加速梯度下降的速度

GLU（Gated Linear Unit，门控线性单元）

传统神经元例如RELU直接就能根据输入值计算输出值，线性变换部分wx+b并不属于神经元的工作，一个层分为线性变换+非线性函数两部分，例如$relu(WX+b)$，这两部分可以独立存在，和在一起构成了一层网络。
但是GLU不一样，他本质并不是一个简单的神经元，他其实是一层完整的网络，$\sigma (WX+B_1)\otimes (VX+B_2)$。它其实是两个线性变换+两个非线性函数。
所以看起来比较和原来不一样。
GLU(Gated Linear Unit) 门控线性单元
使用pytorch动手实现完整的GLU层
gated_cnn
很疑惑的是，论文原文确实用到了卷积这个词，比如输入是$N\times m$，$W$的维度却是$k\times m\times n$，那这个输出肯定就是$k\times N\times n$，这$k$干嘛使得，这个输出没法当输入再输入下一层GLU里啊？但是看了看github的实现，这东西就像卷积的通道数目一样，而且还是要做flatten的，要不下一层确实没法输入，或者直接将K看做1
从Swish到SwiGLU：激活函数的进化与革命，qwen2.5应用的激活函数
大模型系列：SwiGLU激活函数与GLU门控线性单元原理解析
大模型基础｜激活函数｜从ReLU 到SwiGLU

卷积神经网络CNN

卷积神经网络(CNN)模型结构
卷积神经网络(CNN)前向传播算法
卷积神经网络(CNN)反向传播算法
$z^L$是第$L$层的输入，$a^L$是第$L$层的输出
cnn 系列文章三 ----strides，padding详解，基于andrew ng的DeepLearning
极简解释inception V1 V2 V3 V4
Feature Extractor[Inception v4]
卷积神经网络的网络结构——Inception V4
为什么resnet效果好
为什么ResNet和DenseNet可以这么深？一文详解残差块为何有助于解决梯度弥散问题。
正向来看，可以把更多信息传递到后面去，另外加深至少不会变差，无非就是学恒等映射呗；反向来看，可以让梯度传递回去
【AI-1000问】为什么现在大家喜欢用3*3小卷积？

感受野

一个隐层的输出来自于原始图像的多少个像素点

RCNN

一文读懂Faster RCNN
Faster RCNN 学习笔记
一文读懂目标检测：R-CNN、Fast R-CNN、Faster R-CNN、YOLO、SSD

分组卷积

分组卷积本质就是稀疏链接，原本一个input为[J,K,L]，输出为[M,N,O]的卷积操作需要O个[3,3,L]的卷积核，每个卷积核与input的所有通道全连接，分组卷积不是这样的，分组卷积是每个卷积核仅仅和一部分通道全连接。

循环神经网络RNN

循环神经网络(RNN)模型与前向反向传播算法
${\delta }^{(t)}=\frac{\partial L}{\partial o^{(t)}}\frac{\partial o^{(t)}}{\partial h^{(t)}}+\frac{\partial L}{\partial h^{(t+1)}}\frac{\partial h^{(t+1)}}{\partial h^{(t)}}$
因为$L$可以看做$L(o^1,...,o^{\tau })$，其中和$h^t$相关的项只有$o^t,o^{t+1}$，这是因为$o^t$是$h^t$的函数，$o^{t+1}$是$h^{t+1}$的函数，$h^{t+1}$是$h^t$的函数。
因此$L$对$h^t$求导可以看做$\frac{\partial L}{\partial h^t}=\frac{\partial L}{\partial o^t}\frac{\partial o^t}{\partial h^t}+\frac{\partial L}{\partial o^{t+1}}\frac{\partial o^{t+1}}{\partial h^{t+1}}\frac{\partial h^{t+1}}{\partial h^t}=\frac{\partial L}{\partial o^t}\frac{\partial o^t}{\partial h^t}+\frac{\partial L}{\partial o^{h+1}}\frac{\partial h^{t+1}}{\partial h^t}$
RNN梯度消失和爆炸的原因
【神经网络】循环神经网络(RNN)的长期依赖问题
图里那三个公式b和O是分开的
长期依赖：$\frac{\partial L}{\partial W_x}$的式子里，需要对全部$S$进行求导，就是导数依赖于全部的输入，并且稍远一点输入，提供的梯度非常小，导致RNN只和最近的输入有关了，这就违背了RNN的初衷。
LSTM加了遗忘门，如果某个门导致了之前的输入被遗忘，那么对于某个位置求梯度，这个梯度就不会传很远，解决了长期依赖。
LSTM模型与前向反向传播算法
$\odot$乘积就是对应项相乘，并且$x^{(t)},i^{(t)},a^{(t)},o^{(t)},f^{(t)},C^{(t)}$都是向量，并且除了$x^{(t)}$是m维的，其余的都是n维的
像RNN一样，直接把上一时刻的输出作为隐状态，但在LSTM的模型里，除了作为输出的隐含状态，又有一个细胞状态
我觉得LSTM可以这样理解：首先LSTM里有三个输入，数据输入$x$，上一时刻输出$h_{t-1}$，以及细胞状态$C_{t-1}$。那么首先是遗忘门，读取$x$和$h_{t-1}$来计算出一个0到1的值$f_t$，用这个值乘以$C_{t-1}$，这一步的意义就好比说根据当前的输入以及上一时刻的输出（或者说隐含状态），此时细胞状态中的百分之多少的信息是对输出有帮助的，如果说$f_t$是0.3，就意味着，为了得到输出，我需要从细胞状态中提取30%的信息；然后输入门就是根据$x$和$h_{t-1}$来计算出了一个值叫做$i\odot a$，这个东西代表了，神经元此时的$x$和$h_{t-1}$之中蕴含了那些信息，那么在状态更新的时候，就用此时的信息加上从上一个细胞状态中提取的有效信息，得到的就是此时的细胞状态了。输出们，根据$x$和$h_{t-1}$和此时细胞的状态，获得输出值。
Keras关于LSTM的units参数，还是不理解?
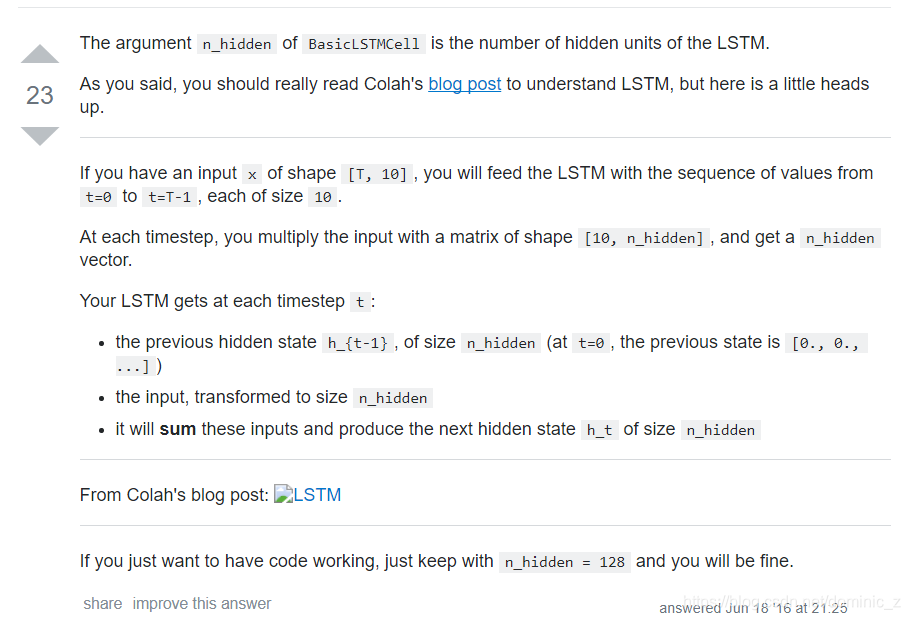
每一个小黄框都可以看做一个单层的前馈神经网络，并且每个小黄框里都有n个神经元，因此输出为n维，这个n就是num_hidden，举例来讲，按照刘建平的blog中的符号定义，遗忘门的输出为$f^{(t)}=\sigma (W_f{h}^{(t-1)}+U_f{x}^{(t)}+b_f)$，那么可以看做一个输入为n+m维，m为输入的维度，输出为n维（即拥有n个神经元）的单层神经网络$f^{(t)}=\sigma ([W_f,U_f{]}^T[h^{(t-1)},x^{(t)}]+b_f)$，那么这个n就是num_hidden

【深度学习】RNN的梯度消失/爆炸与正交初始化
深度学习之GRU网络
GRU是把细胞状态又去除了，用了新的连接方法，留了一个更新门和重置门，更新门的作用，根据上一时刻隐状态和当前输入来决定当前时刻的暂时的隐含状态，重置门的作用有两个根据上一时刻隐状态和当前输入，一方面来决定需要用多少当前时刻的暂时的隐含状态，另一方面决定需要多少上一时刻的隐含状态
这样记吧，用$x,h_{t-1}$计算出了两个值$h^{\prime },h^{\prime \prime }$，他们都是从sigmoid出来的，只是参数不同，其中$h^{\prime }$和$x$结合获得结合隐状态之前的输出，$h^{\prime \prime }$用来更新隐含状态$h_{t-1}$以及输出。最后把更新后的输出和隐含状态求和就可以了

peephole connection
就是把在过各种门的时候，把细胞状态也算上
一文读懂目标检测：R-CNN、Fast R-CNN、Faster R-CNN、YOLO、SSD

Attention

Transformer: NLP里的变形金刚 — 详述
【超详细】【原理篇&实战篇】一文读懂Transformer
自己动手计算Transformer模型参数，深入了解模型内部机制
三万字最全解析！从零实现Transformer（小白必会版😃）
一文教你彻底理解Transformer中Positional Encoding
Transformer 论文精读与完整代码复现【Attention Is All You Need】

从Encoder-Decoder(Seq2Seq)理解Attention的本质
attention score的下标有点问题。意会就行
自然语言处理中的Attention机制总结
首先要根据$s_j,h_i$来计算第$i$个输入的编码的attention score：${\alpha }_{i,j}$，然后对全部输入的编码进行加权求和
attention本质就是权重，在将简单的embedding通过神经网络进行深层表示的过程中，使用attention作为权重，控制深层中语句的表示。只要满足这个，就是attention，softattention是基于输出来作为权重。
但transformer的attention到底attention了个啥，在encoder中，相当于用QK作为权重，从W_v中加权求和输出了深层表示，在decoder中也基于输出进行表示，但是，一句话中不同词之间是没有直接交互的，所以我不能理解一些博客说的，在翻译编码某个词的时候，例如it，注意力会让他注意上下文，让这个it指代上下文的animal，我觉得并没有这个意思，因为attention是attention在W_v身上的，W_v才是用来转化深层标识的工具。

20250513更新：不同词之间有直接交互！！比如一句话有两个token，第一个token算出的q和第一、二个token算出的k向量是有交互的！！q和k是需要做内积作为权重的！！！

各种注意力

一文通透各种注意力：从多头注意力MHA到分组查询注意力GQA、多查询注意力MQA
Qwen2.5的注意力秘籍：解锁高效模型的钥匙，分组查询注意力机制
就是共用参数，多个注意力头共用W_K和W_Q，不同头输出的K和Q自然也就一样了。

Bert

读懂BERT，看这一篇就够了
Transformer的encoder部分堆叠，embedding包含的部分中position embedding是学出来的，比如某个词在句子的第一位，那么他就是取这个position embedding table的第一行embedding，bert分为两个阶段：

1. pretrain阶段：实现完形填空+上下文理解，初具人形；
2. fine-tune阶段：实现具体任务的学习，例如问答等，深入理解；

论文的原图，左侧是预训练阶段，右侧是fine-tune阶段输出不同的模型

BERT 微调实战
对 BERT 进行微调，一般有两种方式：

只微调分类输出头，保持预训练 BERT 大量的参数都不变，只聚焦于我们自己的分类输出头。相当于是 BERT 已经有很多人类的自然语言处理知识了，我们只是告诉它要干什么就够了。

在微调的过程中把 BERT 的参数整体也进行微调。

GPT

【李沐论文精读】GPT、GPT-2和GPT-3论文精读
GPT 系列论文精读：从 GPT-1 到 GPT-4
LLM 系列超详细解读 (二)：GPT-2：GPT 在零样本多任务学习的探索

在gpt1之中，pre-train+fine-tune的方式训练，fine-tune是用于构建具体任务的模型，例如分类、翻译等等，比如说在情感分析中，我们会构建一个样本“我喜欢小狗,I like puppy”，然后告诉gpt这是同一个意思；但是GPT2的训练中，没有了fine-tune这一步，他们认为如果模型真的学会了人类语言，那么他就应该知道这两句话是同一个意思并且一个是中文一个是英文。例如，模型可能会看过一句话：“我喜欢小狗，which translates as I like puppy”。于是gpt2扩大了数据量，并且在下游任务时对模型的输入进行了修改，比如说如果我们希望让模型翻译 I like puppy，那么我们需要输入“translate to chineses,I like puppy”。
GPT模型总结【模型结构及计算过程_详细说明】

Llama

万字长文详解LlaMA 3的前世今生
Llama-1的详细架构只能去看代码了，因为论文里只是非常简单地说：使用了Transformer的decoder，并且在此基础上做了一些优化。（不过这么大的模型估计也没多少人真正去看模型结构，基本都是要拿来就用的）
LLaMA 超详细解读（paper & code）

1. 为了增强训练稳定性，采用前置的RMSNorm[5]作为层归一化方法：就是说对输入直接做了norm
2. 为了提高模型性能，采用SwiGLU作为激活函数：SwiGLU本质是一个网络。原本在Transformer的FFN前向层中，原本是ReLU(W1X+b1)W2+b2，其实就是一层“全连接+非线性变换+全连接”，将这个“全连接+非线性变换+全连接”变更成SwiGLU网络了
3. 为了更好地建模长序列数据，采用RoPE作为位置编码：看吐了

RoPE

这里用到了复数的知识，相当于将使用复数运算来简化向量运算。例如可以将一个二维向量表征成$a+bi$，然后用这个复数来实现旋转。也可以通过复数来求两个向量的点积，两个二维向量表征成复数然后相乘取实部就是点积。

十分钟读懂旋转编码（RoPE）
Rotary Position Embedding (RoPE, 旋转式位置编码) | 原理讲解+torch代码实现
再论大模型位置编码及其外推性（万字长文）
RoPE旋转位置编码深度解析：理论推导、代码实现、长度外推
关键就在于理解$<f(q,m),f(k,n)>=g(q,k,m-n)$的含义，$f(q,m)$代表的是原始的查询向量$q$嵌入位置（第m位token）向量后的输出，与传统transformer不同，传统transformer是在计算qkv之前做位置嵌入，而rope是在计算qkv之后根据位置做嵌入$f(q,m)$。

$<f(q,m),f(k,n)>$代表位置嵌入后的查询向量和键向量内积，其实就是attention score了。但要求这个attention score能够表示成g(q,k,m-n)，代表这个attention score是嵌入位置向量之前的查询向量、键向量以及相对位置的函数，如果等式成立，那么就达到了两个目的：1. 这个attention score中的位置向量只和两个token的相对位置有关（transformer的位置向量似乎不具备这个性质），这是相对位置编码的特性；2. 每个位置嵌入向量只和当前的位置有关，这是绝对位置编码的特性。

RoPE给出的方法就是利用复数的方法，怎样证明的我没看懂，大体思路是这样的：先假设q、k是二维的，发现二维向量乘以旋转矩阵（讲解中的cos/sin矩阵，相当于让向量在二维空间做旋转）作为f就可以满足上面这个等式。然后扩充到k维度也一样，看做成多个二维向量就好了。
知乎回答的LLAMA中的实现的两个方法，就是回答中的$R_{\theta ,m}^{d}x$的高效计算方法的代码，只不过用了复数来辅助运算。先计算了$m{\theta }_0,m{\theta }_1,m{\theta }_2$，然后通过torch.polar映射到复数快速计算cos与sin，在apply_rotary_emb里也是先将q、k映射到复数空间，在复数空间做乘法运算，然后计算q_out,k_out，用jupyter notebook跑个demo就可以了。

import torch

def precompute_freqs_cis(dim: int, seq_len: int, base: float = 10000.0):
    # reqs.shape = [dim//2]，[theta_0,theta_1,...,theta_{dim-2}]
    freqs = 1.0 / (base ** (torch.arange(0, dim, 2)[: (dim // 2)].float() / dim))
    # 生成 token 序列索引 t = [0, 1,..., seq_len-1]
    t = torch.arange(seq_len, device=freqs.device)
    # 外积，freqs.shape = [seq_len, dim // 2]，
    # 输出就是[[0,...,0],[1*theta_0,...,1*theta_{dim-2}],...,[(seqLen-1)*theta_0,...,(seqLen-1)*theta_{dim-2}]] 
    freqs = torch.outer(t, freqs).float()  # 计算m * \theta

    # 计算结果是个复数向量，第一个参数代表向量长度，第二个参数代表向量角度。
    # 映射到复数假设 freqs = [x, y]
    # 则 freqs_cis = [cos(x) + sin(x)i, cos(y) + sin(y)i]
    # 输出就是[[cos0+i*sin0,...,0],[cos(1*theta_0)+j*sin(1*theta_0),...],...]
    # shape: [seqLen,dim//2]
    freqs_cis = torch.polar(torch.ones_like(freqs), freqs) 
    return freqs_cis


# 旋转位置编码计算
def apply_rotary_emb(
    xq: torch.Tensor,
    xk: torch.Tensor,
    freqs_cis: torch.Tensor,
) -> Tuple[torch.Tensor, torch.Tensor]:
    # xq.shape = [batch_size, seq_len, dim]
    # xq_.shape = [batch_size, seq_len, dim // 2, 2]
    xq_ = xq.float().reshape(*xq.shape[:-1], -1, 2)
    xk_ = xk.float().reshape(*xk.shape[:-1], -1, 2)
    
    # 转为复数域，最后两个维度变成实部和虚部，shape:[batch_size, seq_len, dim // 2]
    # [[[x0+j*x1],[x2+j*x3],...,[x_{dim-2}+j*x_{dim-1}],...],...]
    xq_ = torch.view_as_complex(xq_)
    xk_ = torch.view_as_complex(xk_)
    
    # freqs_cis也是[seqLen,dim//2]，对应项相乘，例如(x0+j*x1)*(cos0+i*sin0)=x0cos0-x1sin0+(x1cos0+x0sin0)j，刚好就是fq函数的计算结果
    # 应用旋转操作，然后将结果转回实数域
    # xq_out.shape = [batch_size, seq_len, dim]
    xq_out = torch.view_as_real(xq_ * freqs_cis).flatten(2)
    xk_out = torch.view_as_real(xk_ * freqs_cis).flatten(2)
    return xq_out.type_as(xq), xk_out.type_as(xk)

AutoEncoder

深度学习教程之Autoencoder
栈式自编码算法
层数越深的隐层输出代表着越高级的特征
为什么稀疏自编码器很少见到多层的？ - 科言君的回答 - 知乎
几种Autoencoder的深入理解和思考

变分自编码器 VAE

变分自动编码机(VAE)理解和实现(Tensorflow)
变分自编码器（一）：原来是这么一回事
李宏毅VAE
A实现-hwalsuklee/tensorflow-mnist-VAE
B实现-VAE-TensorFlow/blob/master/main.py
GITHUB上的vae实现很多，对于loss的定义不太一样，具体实现细节也不同
上面A和B的实现有两个区别
首先是encoder输出的值是什么有点区别
A实现中encoder输出的是均值mu和标准差sigma，而为了保证标准差为正，实现中在encoder的实现过程中，使用了softplus，如下

而B实现中，encoder的输出是mu_encoder和logvar_encoder，前者就是期望，而后者并不是是标准差，下面这个std_encoder才是标准差，也就是说$logvar\_encoder=2\ast log(std\_encoder)$

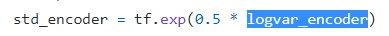
所以在KL散度的定义中，A实现的定义方式如下

B实现的定义方式如下

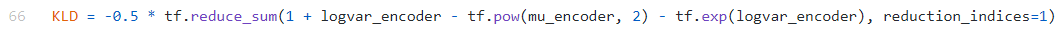
可以看出他们实际上是一样的
另外，在似然损失的定义方面也有不同
A实现的似然损失是手动写的

B实现的定义方式用了个内置的损失函数

sigmoid_cross_entropy_with_logits这个函数是交叉熵，里面带负号的
所以A实现里损失的定义

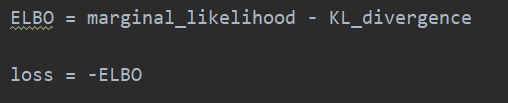
和B实现里的损失的定义

也是一样的，TMD看了一下午终于看明白了
另外我原本以为，这个似然损失可以改成均方误差，后来发现好像又不可以，因为这个是似然

对抗自编码器 AAE

对抗自编码器：Adversarial Autoencoders
图里的+和-不是加减，而是正样本和负样本的意思
hwalsuklee/tensorflow-mnist-VAE

word2vec

特征提取方法: one-hot 和 TF-IDF
词袋模型（BOW，bag of words）和词向量模型（Word Embedding）概念介绍
word2vec原理(一) CBOW与Skip-Gram模型基础
讲的一般，而且描述有一些不清楚，看斯坦福大学的课件吧，写的很好，简单说就是三层网络加一个softmax，第一层输入，经过线性变换组合作为第二层的输入，第二层输入什么输出什么，然后再经过一个线性变换作为第三层的输入，第三层是也是输入什么就输出什么，比如说第i个神经元输出为$z_i$，然后末尾用softmax计算后得到最终的输出，第i个最终输出就是$e^{z_i}/{\sum }_j{e}^{z_j}$
word2vec原理(二) 基于Hierarchical Softmax的模型
传统三层网络输出的softmax的计算的时候，需要计算每个输出值$z_i$的$e^{z_i}$，但是这计算量很大，而分层softmax就是为了避免这个事。怎么避免的呢，就是通过一个霍夫曼树，它是这样设计的，它首先随机初始化词向量，并且这个词向量随着迭会更新；然后对输入求平均，作为隐层的输入，同时也是输出，这其实就是CBOW在做的事，一个字串是$x_{w-c},...,x_w,...,x_{w+c}$，其中每个$x$都是当前时刻的词嵌入向量，然后$h_w=\frac{1}{2c}{\sum }_{i=-c,i\ne 0}^c{x}_{w+i}$作为隐层的输入与输出；然后把输出送到一个霍夫曼树的根节点，注意如果此时我们希望的是，这个霍夫曼树能够把$h_w$送到$x_w$对应的词在树中的位置去。这样我们就不用计算全部值的softmax了，只算结点的sigmoid就行了。
那什么时候算训练好了呢，就是在当前的词向量与当前霍夫曼树的情况下，多数的词都能被送到正确的位置，就可以了。最终的词向量就是我需要的词向量。而这个霍夫曼树em。。。应该就没啥用了。
如果一个词对应多种上下文怎么办呢，没关系，你看第三小节的步骤3，他是用单个样本进行参数更新的。
文中提到了首先随机初始化词向量，这个可以结合TensorFlow的word2vec示例理解，输入是one-hot，过一个embedding，中间层的输入就是输出
word2vec原理(三) 基于Negative Sampling的模型
有点不好理解奥，刚开始对${\theta }^{w_i}$是什么没太理解，但是博主45楼回复了，然后更新就完了

二刷理解：以skip-gram为例，输入一个词$w_0$返回上下文$context(w_0)$，可以想象成输入层是一个词的one-hot编码；过了一个embedding层之后可以获得一个嵌入向量$x_0$，然后在embedding层后面又接了一个全连接网络，输出的维度是字典大小，用这个$x_0$过这个全连接，可以获得$\sigma (x_0^T{\theta }^{w_i})$（不要在意x是列向量还是行向量，意会就行），就相当于一个logistics regression，代表着$w_0$的context里有$w_i$的概率。然后在梯度下降的时候，只需要计算正样本出现的概率和负样本不出现的概率就可以了，也不用过softmax，最大化似然就可以了，省了很多计算
三刷疑问：文中说$w_0,context(w_0)$作为正样本，$w_i,context(w_0)$作为负样本，但我看Distributed Representations of Words and Phrases
and their Compositionality
论文里并不是这样啊，论文里的意思是，中心词不动$w_I$，只不过是对context进行修改，以$\frac{count(w_i{)}^{3/4}}{\sum _{u\in vocab}count(u{)}^{3/4}}$作为词$w_i$的概率进行采样，修改context里某个位置的词，然后计算损失，或者说最大化目标为$log\sigma (v_{w_o}^{\prime T}{v}_{w_I})+E_{w_i\sim P(w)}log(\sigma (-v_{w_i}^{\prime T}{v}_{w_I}))$，其中$v_{w_I}$是输入层的词向量，$v_{w_i}^{\prime }$是输出层的嵌入矩阵的对应的词向量，第一项中$\sigma (v_{w_o}^{\prime T}{v}_{w_I})$代表context里存在$w_O$的概率，$\sigma (-v_i^{\prime T}{v}_{w_I})$代表不存在$w_i$的概率
Embedding之word2vec
对边缘词没有做padding

玻尔兹曼机

深度学习教程之受限玻耳兹曼机
受限玻尔兹曼机（RBM）原理总结

小样本

Deep Learning Architectures That You Can Use with a Few Data

深度信念网络

深度信念网络(Deep Belief Network)
深度信念神经网络DBN最通俗易懂的教程
机器学习——DBN深度信念网络详解

GAN

生成式对抗网络GAN
我觉得生成网络的input应该是有意义的，不应该是随机数，例如每个input的第一维来自一个分布，代表着生成数字是1的概率。
分类模型应当是固定的，否则两个模型并行训练很容易两个模型都是废的。

损失

Triplet Network, Triplet Loss及其tensorflow实现