cnn 系列文章三 ----strides，padding详解，基于andrew ng的DeepLearning

cnn系列文章二 –初识滤波器

惯例，还是分享一句歌词呢。

《诗话小镇》
岁月如流沙苍老了风华
那誓言未长大
流年斑驳眉心朱砂
你画上哪个她
繁华褪尽薄了红纱

约定符号：

• 输入图像： $n \times n$
• 过滤器： $f \times f$
• paddig(填充)： $p$

• stride(步长): $s$

  padding

1. padding概念引入

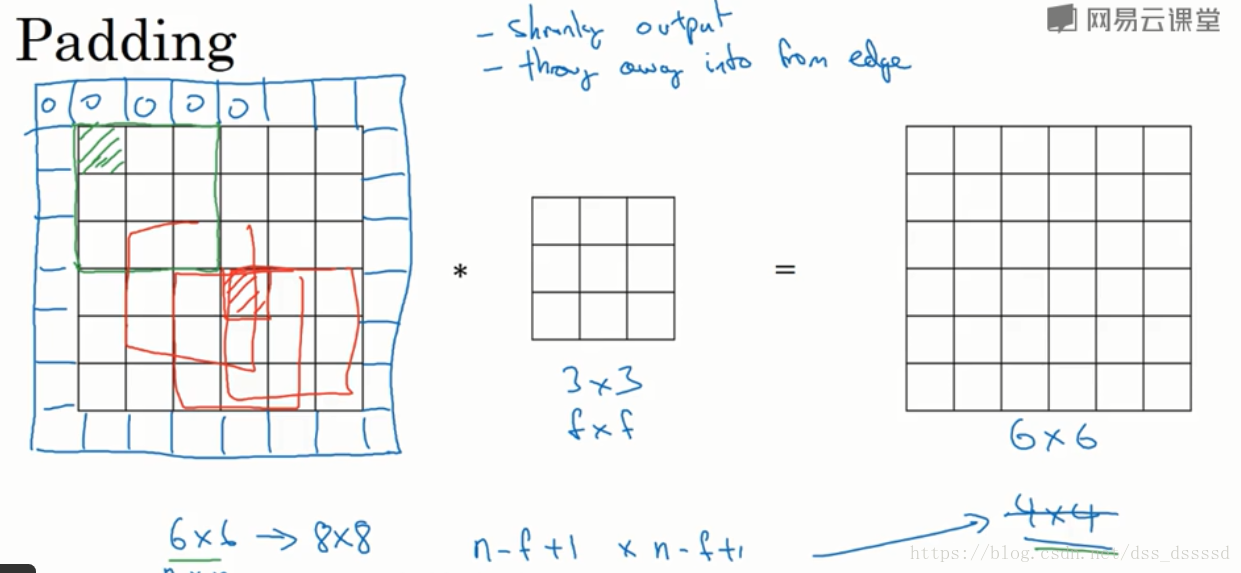
当使用一个$3 \times 3$的过滤器对$6 \times 6$的图像进行卷积操作后，会得到$4 \times 4$的输出图像。
此时输出图像大小为：

$$(n - f + 1) \times (n - f +1)$$
但是这样会带来两个缺点：

1. 图像会越来越小
2. 如上图，原图像左上角绿色区域纸杯一个过滤器使用，而中间红色区域会被多个过滤器使用，这就意味着边缘信息的丢失

为此引入padding（填充）的操作，即在卷积操作之前，先在图像边缘进行像素填充，像素值可以是0也可以是图像边缘像素，填充宽度为p，例如在上图中使用像素0对图像边缘填充，宽度p=1，此时输出图像和输入图像维度相等，并且图像左上角的像素被多个过滤器使用，边缘信息丢失的更少。
此时，输出图像的维度为：

$$(n - f + 2p +1) \times (n - f +2p +1)$$

2. padding填充模式

1. padding=’VALID’

   此时$p = 0$,即不填充， 输出图像为$(n - f +1) \times (n - f +1)$

2. padding=’SAME’

   此时输入和输出图像维度相同，此时:
   

   $$p=\frac{f-1}{2}$$
   因为 $n - f + 2p + 1 = n$

   注意： 一般 $f$为奇数，主要有两个好处：

   • p可以取整数
   • 奇数过滤器有一个中点,也称锚点(anchor),便于确认过滤器的位置

stride (卷积步长)

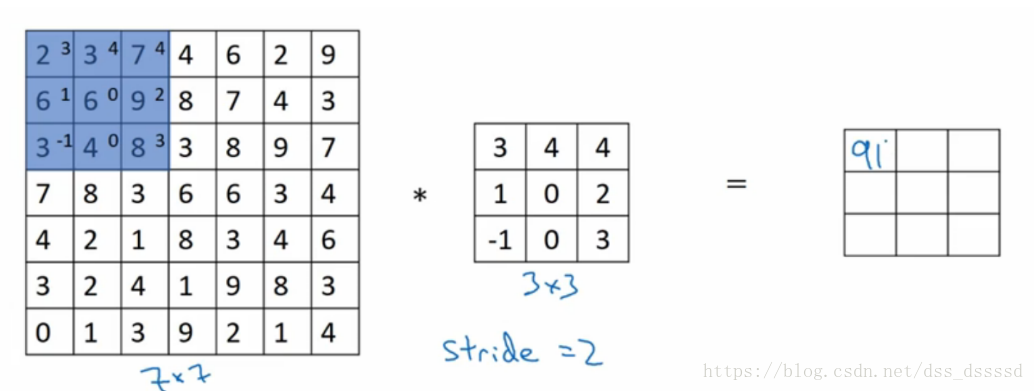
不同于之前一次想左移动一格，此时向左移动两格，

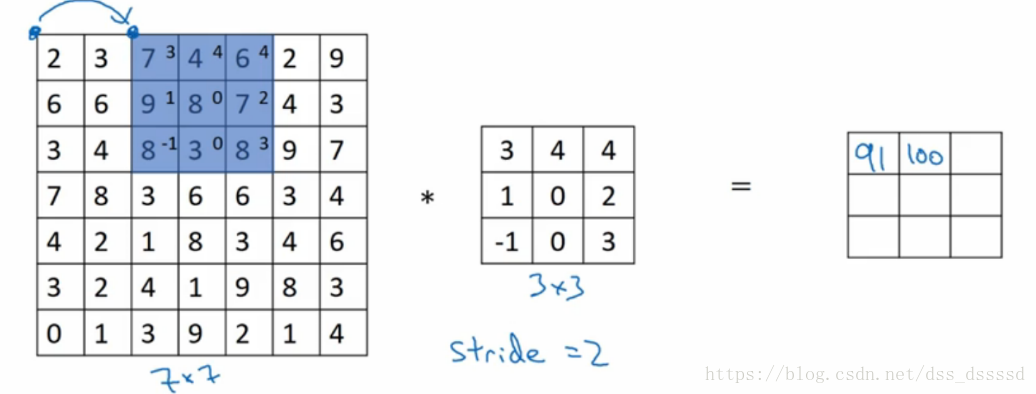
同样的，也是向下移动两格

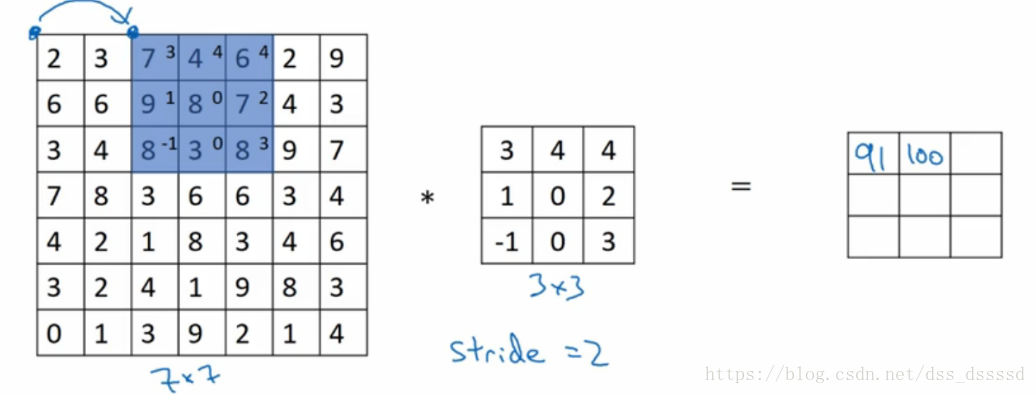
最终的输出图像大小为$3 \times 3$

假设stride移动步长为s，则最后的输出图像为：

$$\lfloor( \frac{ n + 2p - f}{s} + 1 )\rfloor \times \lfloor( \frac{ n + 2p - f}{s} + 1 )\rfloor$$
其中， $\lfloor \rfloor$为向下取整

比如上图中：

$$\lfloor( \frac{ 7 + 2 \times 0 - 3}{2} + 1 )\rfloor \times \lfloor( \frac{ 7 + 2 \times 0 - 3}{2} + 1 )\rfloor = 3 \times 3$$

GRB多通道图像的卷积

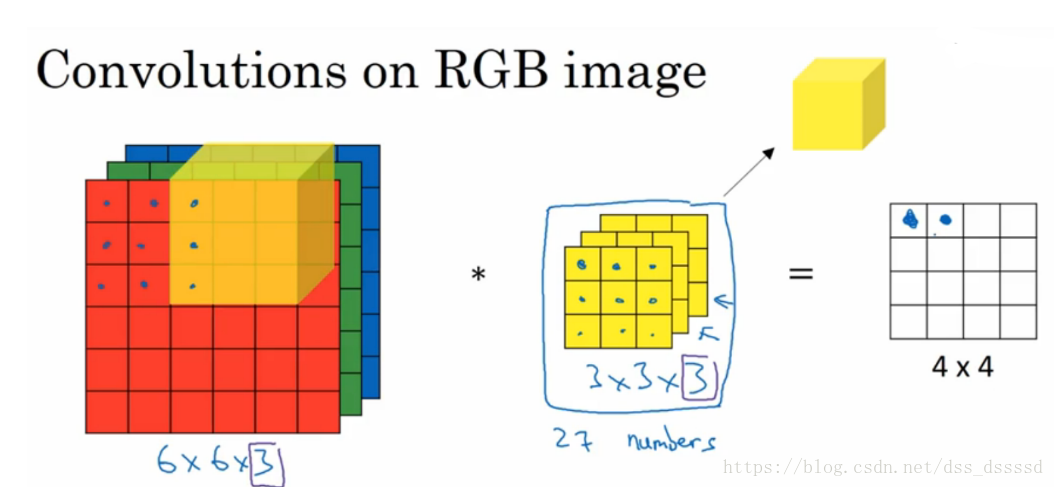
比如在$6 \times 6 \times 3$,过滤器的大小不在是$3 \times 3$而是$3 \times 3\times 3$，最后的3对应为通道数（channels）。

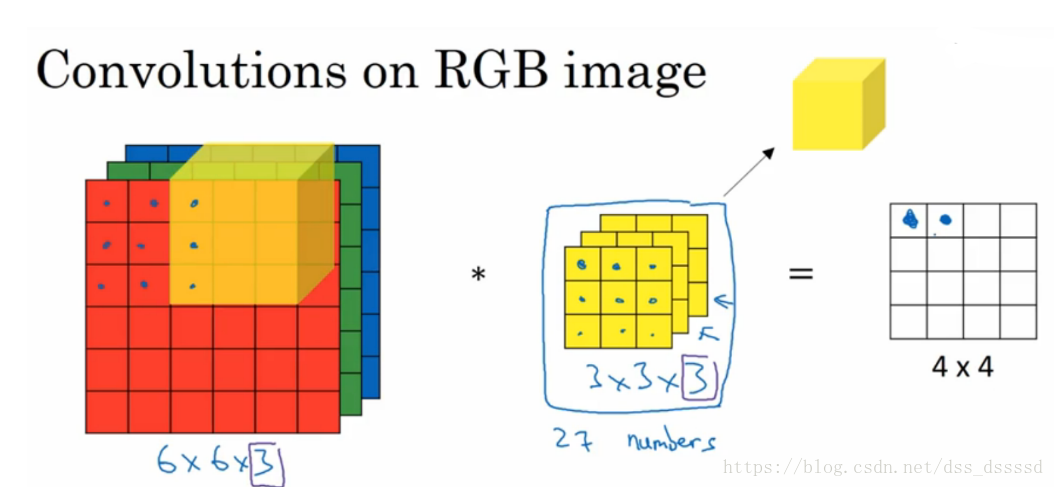
卷积过程：比如第一个$3\times3$与R通道卷积，会得到一个数，同理，第二个$3\times 3$与G通道卷积，第三个$3 \times 3$与B通道卷积，然后将三个数累加，作为$4 \times 4$的左上角第一个位置值，接下来依次在图像上滑动，最终得到$4\times4$的输出。

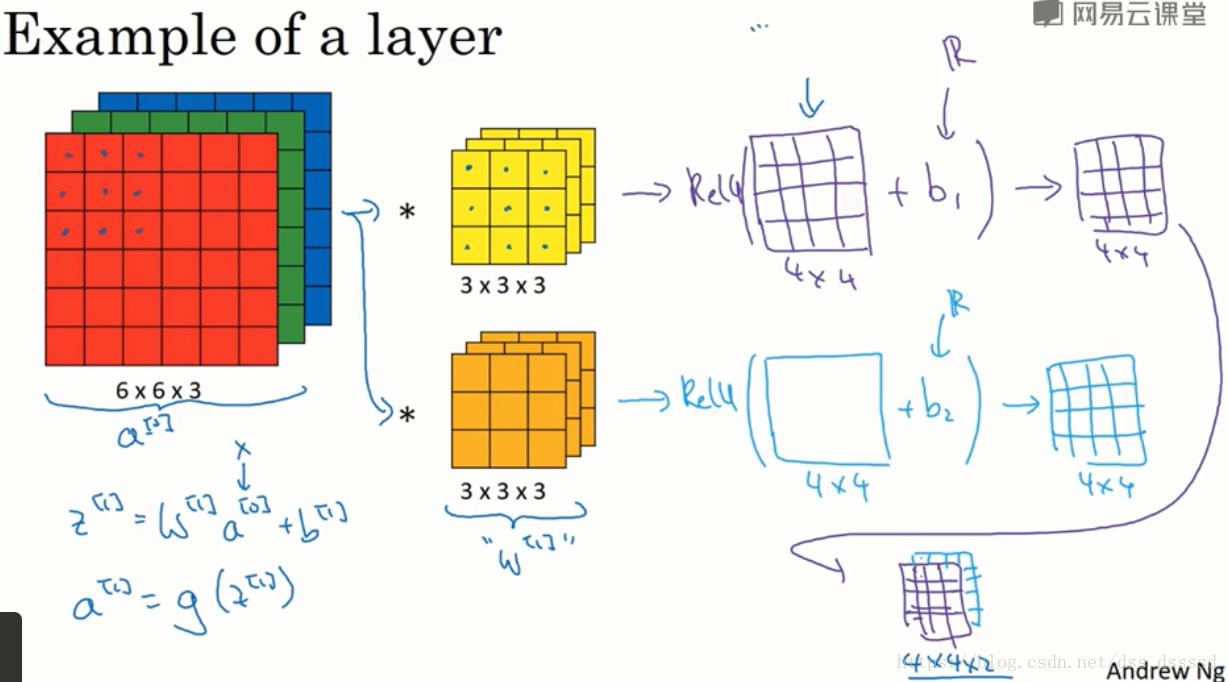
我们肯定不能只在图像中检测一种特征，而是同时要检测水平，垂直，45度边缘等特征，此时就要使用多个过滤器了。假设我们使用两个过滤器，最终的输出为$4 \times 4\times2$,这里的2是使用两过滤器的结果，同样，若是使用5个过滤器呢？输出结果就是$4\times4\times 5$了。下面是计算的例子：

单层卷积

上一节，得到两个$4\times4$的矩阵，通过python的广播机制在两个矩阵上加入偏差bias，然后经过非线性函数relu，即可得到单层卷积网络的输出。
图示如下：

公示表示如下：

$$z^{[l]} = a^{[l-1]} \ast f^{[l]} + b^{[l]}$$
$$a^{[l]} = Relu(z^{[l]})$$

式子中$a^{[l]}$标识第$l$层的输出，$f^{[l]}$标识第$l$层的过滤器，$b^{[l]}$标识第$l$层的偏差

下面是动态计算的例子，跑的有点快，得计算一下,

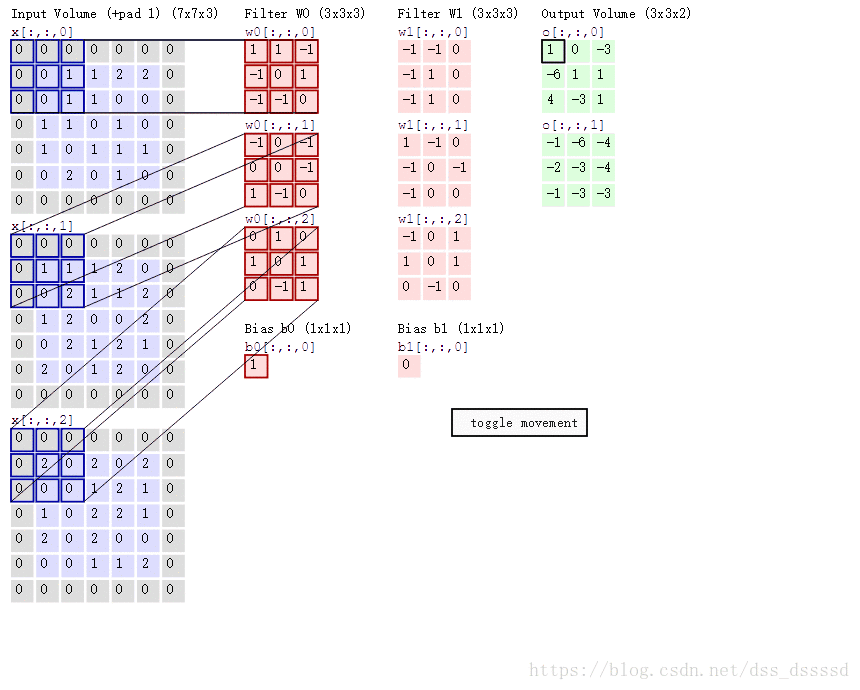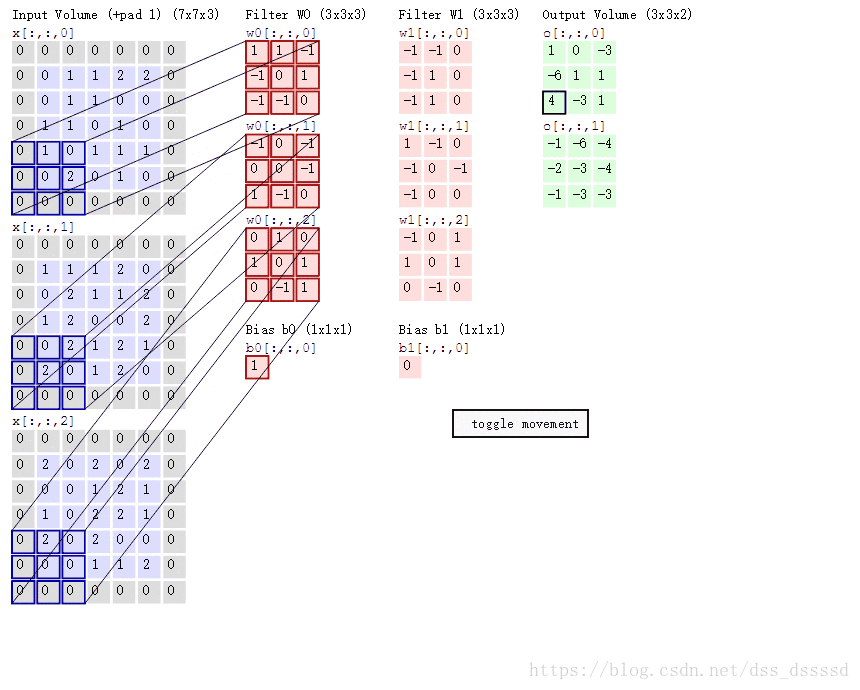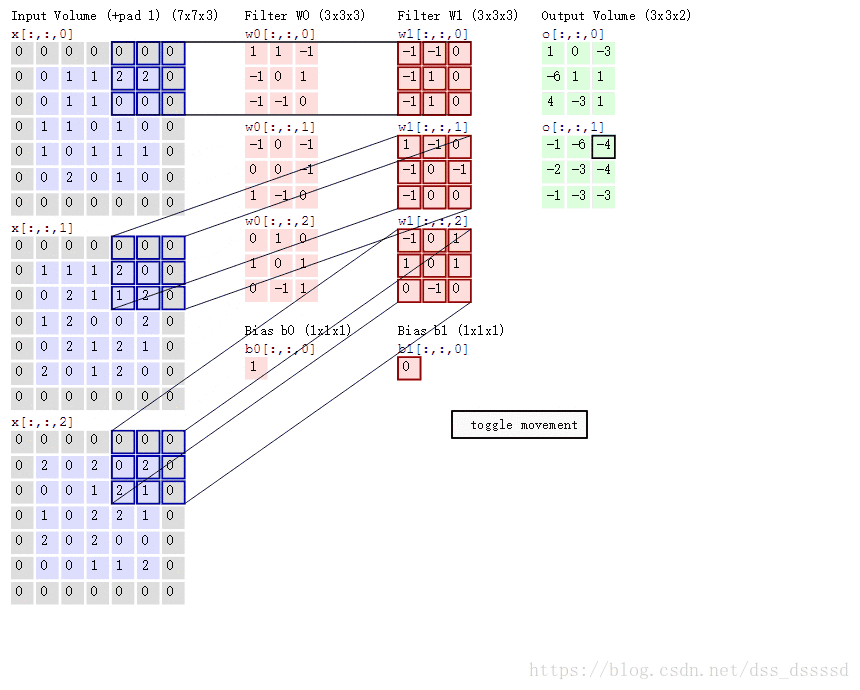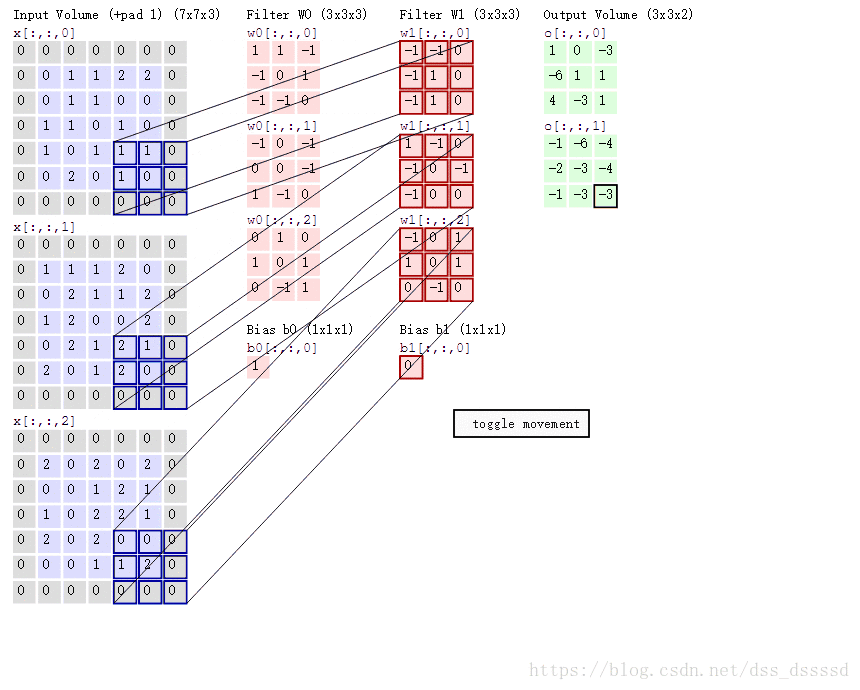
比如：输出O[:,:,0]的左上角第一个值：

$$1 =( 0 \times 1 + 0 \times 1 + 0\times -1 + 0\times-1 +0\times0+1\times1+0\times-1 +0\times-1+1\times0) + (\cdots) + (\cdots) + 1 = 1 +-1 + 0 +1$$

本系列课程的符号约束

1. 过滤器需要四个参数确定：

   $$宽度 \times 高度 \times 通道数 \times 过滤器个数$$
   其中，通道数与上一层图像输入的通道数相同，过滤器个数与本层输出图像的通道数相同。这一部分在下面的例子中会有深刻体现，并且在tensorflow函数调用中要明确指明的参数。

2. 符号约定
   对于第$l$层神经网络层：

   • $f^{[l]}$:第$l$层过滤器大小，$f \times f$

   • $p^{[l]}$:第$l$层填充数量 $p$
   • $s^{[l]}$: 第$l$层步长大小 $s$

   • $n_C^l$: 过滤器的个数

   • input:

     $n_H^{l-1} \times n_W^{l-1} \times n_C^{l-1}$:$l-1$层输入图像的高宽以及通道数

   • output:

     $n_H^{l} \times n_W^{l} \times n_C^{l}$: 输出图像的高、宽以及通道数

   • 输出图像的大小：
     
     • $n_H^l = \lfloor \frac{n_H^{l-1} +2 \times p^{[l]} - f^{[l]} }{s^{[l]}} + 1 \rfloor$
     • $n_W^l = \lfloor \frac{n_W^{l-1} +2 \times p^{[l]} - f^{[l]} }{s^{[l]}} + 1 \rfloor$
     • 输出图像通道数就是过滤器个数： $n_C^l$

将输出的图像加上Bias然后经过非线性函数Relu即可完成一层卷积神经网络的构建了。

简单卷积神经网络实例

建议在此部分自己找张纸推导一遍，我当时跟着课程推导了两三个网络实例。

最后将第三层的输出通过softmax或logistic来进行相应的操作

在这个网络结构中，有两个参数的变化值得注意：

• 图像宽度变化 $39 \to 37 \to 17 \to 7$
• 图像通道数变化 $3 \to 10 \to 20 \to 40$

图像宽度逐层减半而图像通道逐层增加，关于这些超参数的确定，后边会给出一些建议

接下来讲解池化层以及卷积神经网络的架构